-
UID:317649
-
- 注册时间2020-06-19
- 最后登录2026-02-11
- 在线时间1927小时
-
-
访问TA的空间加好友用道具

|
1.摘要 IN2F�O/Y�@
�G��b]t%\�
z��)$�X/v�
在测量信号或数据的情况下,很难(如果不是不可能的话)完全避免所有可能的噪声源,因为这些噪声源会干扰任何实验测量。但是,噪声的存在会干扰数据的重要特征(例如,测量光谱的半宽谱)。 �9�Tbi_6�[
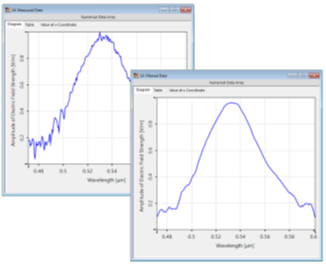
因此,有一些后期处理技巧可能会有所帮助。这里我们只讨论一个这样的工具:Savitzky-Golay滤波器,它通过对一组采样点执行回归算法来平滑局部噪声。在这个例子中,我们讨论了VirtualLab Fusion中这个特性的选项和效果,并以一个绿色LED灯在60 nm带宽下发射的光谱为例进行了测试。 (9�bFIv�Mc
cnfjO�g'\{
 8:V:^`KaSs -A}U^-�'a} 2.如何进入Savitzky-Golay过滤器 � �#P8R�� 8:V:^`KaSs -A}U^-�'a} 2.如何进入Savitzky-Golay过滤器 � �#P8R��
P�h(�bgQg
+[$���d9��
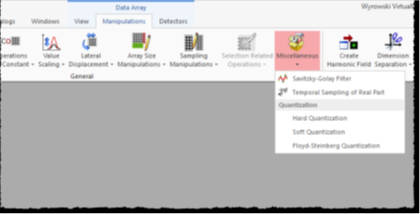
对于每个实值数据数组,都可以在下面找到Savitzky-Golay滤波器 u�zA"+c�V5
操作→ �\OMWE/qMy
杂项→ hVPSW# .�d
Savitzky-Golay过滤器 H4�#|f� n�
S+LE ASOr�
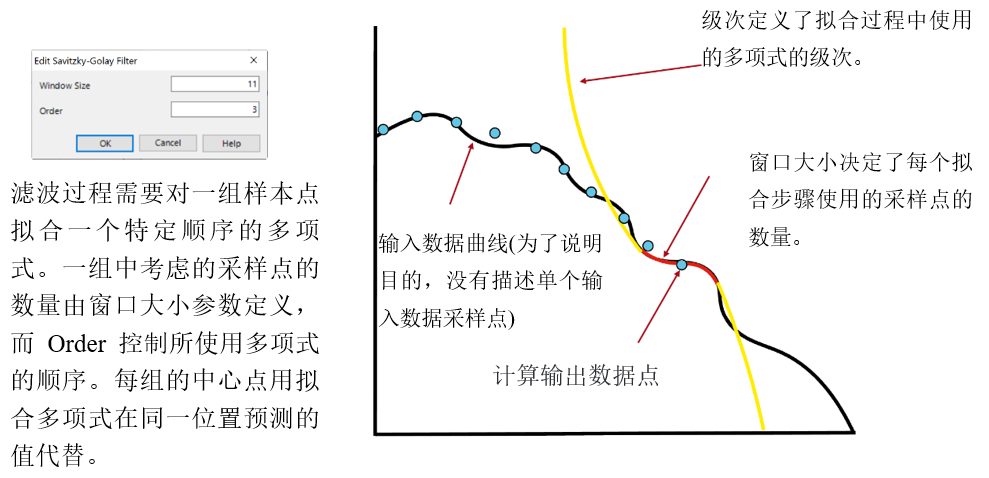
 �jr$�]k�LY DpG�|Kl�|d 3.可视化的过滤函数 .32]�$v�x� �jr$�]k�LY DpG�|Kl�|d 3.可视化的过滤函数 .32]�$v�x�
B�fmSM��9
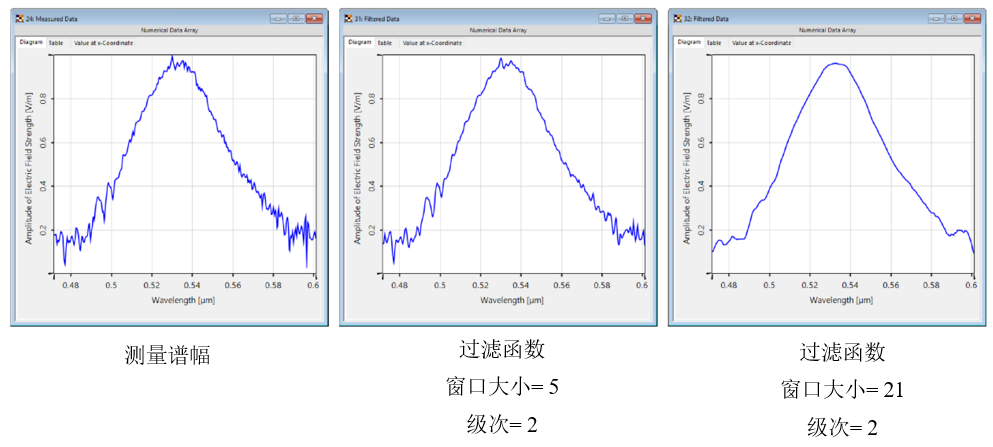
 "/�v{B?~%! |�FK�##�8� 4.影响过滤器-窗口大小 |��> mx�*G "/�v{B?~%! |�FK�##�8� 4.影响过滤器-窗口大小 |��> mx�*G
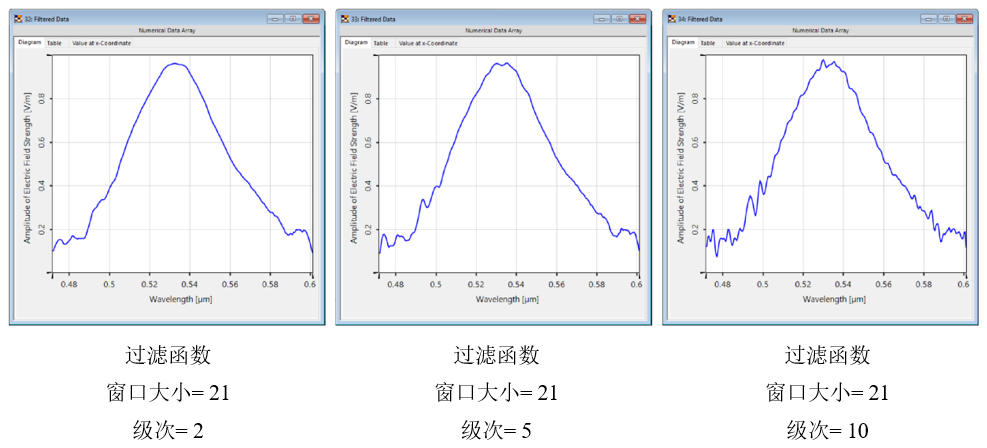
Jr/|nhGl5 更大的窗口大小导致在拟合过程中考虑更多的采样点,因此曲线更平滑。 </,RS5u�kn
c�fn\D�e%.
 ^��,��`�;x o�5(`7XV6D 更高的阶数允许更详细的曲线,但反过来也可以保留局部噪声。 ~s_n\�r&23 ^��,��`�;x o�5(`7XV6D 更高的阶数允许更详细的曲线,但反过来也可以保留局部噪声。 ~s_n\�r&23
q���F9z@�a
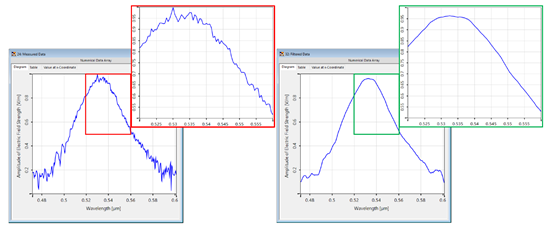
 5�.st!�Lp1 i@���7�b� 5.局部噪声过滤 �rSGp]�W|� 5�.st!�Lp1 i@���7�b� 5.局部噪声过滤 �rSGp]�W|�
o���/uA_19
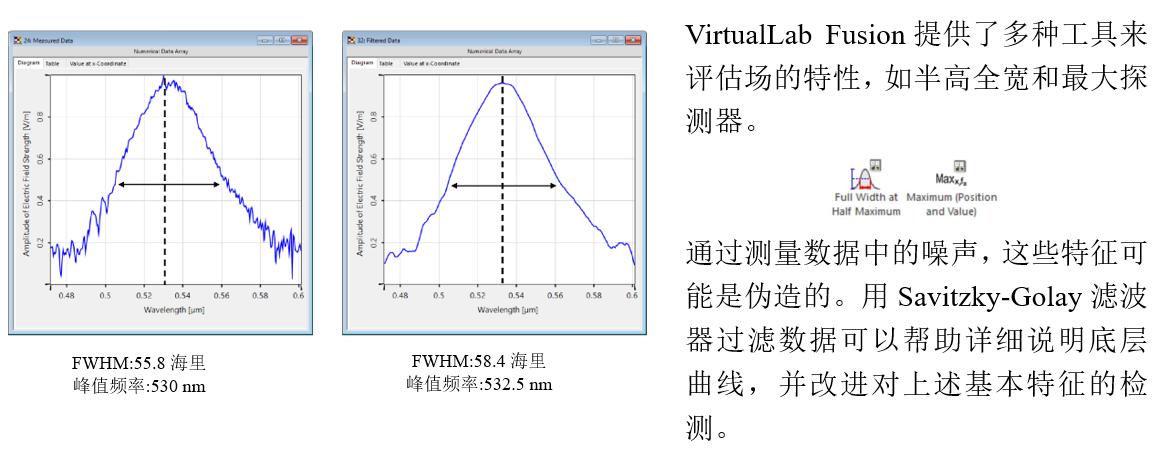
 �UOT�M>d1P \-A=??��@H 6.FWHM 检测 k)+2+h�X&> �UOT�M>d1P \-A=??��@H 6.FWHM 检测 k)+2+h�X&>
�Z�Ms$C3��
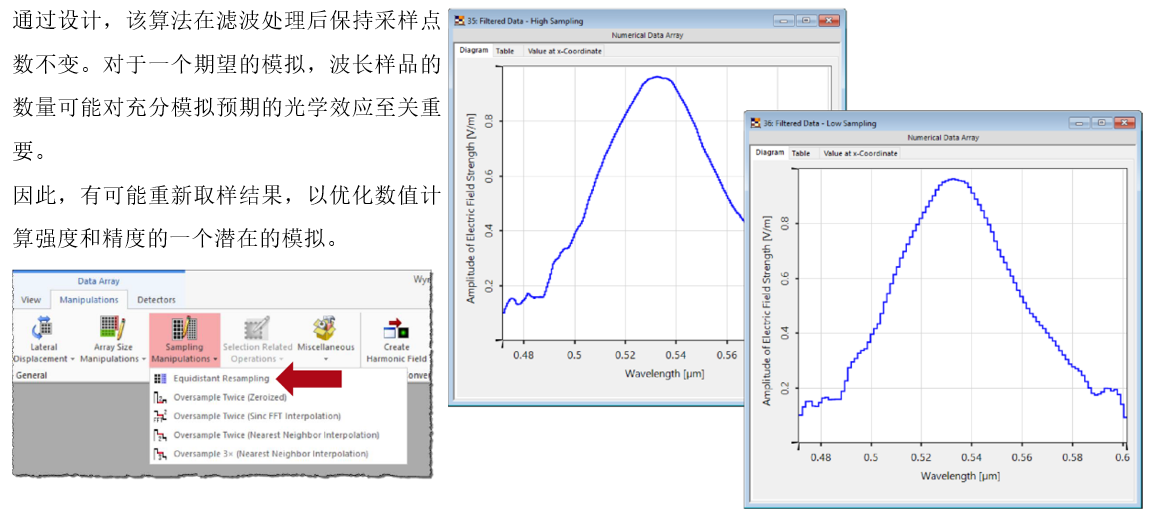
 �9|19ia@[\ �)%e`�SGmp 7.等距的重采样 l���#!p�?l �9|19ia@[\ �)%e`�SGmp 7.等距的重采样 l���#!p�?l
p�-�d2H�Xo
 7�v9l+OX,6 7�v9l+OX,6
|