VirtualLab Fusion包含了多种场求解器和函数。它们可以在空间(x)域或空间频率(k)域工作。为了将不同的求解器和函数简建立连接,实现复杂
系统的建模,x域和k域之间的转换是至关重要的一步。 在本文中,我们将通过不同
实例的讨论来示范如何对VirtualLab Fusion中有三种傅里叶变换算法进行设置。
�_&s�37A&\
V_*T��Y�6  �S EdNH.|I NsY�eg&>`� 2. 三种傅里叶变换 zRDBl02v$T _bp9U��J�� ��z����x��
�S EdNH.|I NsY�eg&>`� 2. 三种傅里叶变换 zRDBl02v$T _bp9U��J�� ��z����x�� 快速傅里叶变换(FFT)
z>HeM
M�ei - 对于不同数值计算,一种
标准而高效的算法。
�|/�B�2B�m 半解析傅里叶变换(SFT)
-x�i]~�svg - 一种无需近似的高效重构。
noz&4"S.{� - 二次相的解析处理,类似chirp-z变换。
B 14Ziopww i6F`�KF'i& 逐点傅里叶变换(PSF)
�=s�VB�.�P - 受静态相位理论启发的一种近似方法,但采用纯粹的数学形式来表达。
�:Z�0m�� " - 对强波前相位是一种高效而精准的方法。
>W��%tE�c� ?�ysC7��(( _�B4H"2}[Y  �Nby�VBl0= D�k&@AjJga 3. 每个元件的设置 8j�yg1NN D ���q�F!�oP *G|w#-\.c�
�Nby�VBl0= D�k&@AjJga 3. 每个元件的设置 8j�yg1NN D ���q�F!�oP *G|w#-\.c� 傅立叶变换设置
��e-vw�v�e - 对于每个元件和
探测器,都可以使用 “傅立叶变换”选项卡。
z��)$�X/v� - VirtualLab Fusion自动选择所有激活的傅立叶变换选项;不选择未激活的选项。
v{�7Jzjd�� - 傅立叶变换的组合影响自由空间中向前传播过程的建模。(这意味着不仅适用于元件前面的自由空间——它也适用于具有复杂通道配置的情况)
Cf#�[E~2�4 6{/HNE�I*1 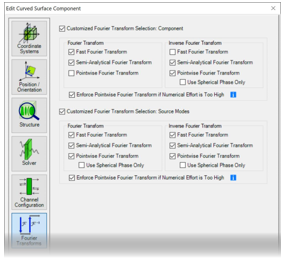 �-ZXC^�zt� /�$�v0Rq�9 4. 每个元件的设置 ��~5e)�h_y �mouLj�T&p
�-ZXC^�zt� /�$�v0Rq�9 4. 每个元件的设置 ��~5e)�h_y �mouLj�T&p 傅里叶变换设置
O���m��O/x *^]H��qf(` 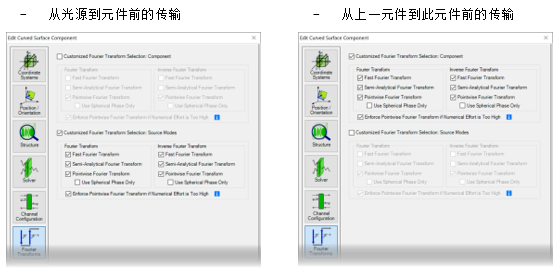 #k���D8U# FF]xwptr�x 5. 默认的傅里叶变换设置 A�8bDg:G1i I�yvJwrO �l*;Isz:��
#k���D8U# FF]xwptr�x 5. 默认的傅里叶变换设置 A�8bDg:G1i I�yvJwrO �l*;Isz:��
光源模式和探测器的设置
�+�D
,Nd=/ - 对于光源模式和探测器,默认情况下将激活所有三个傅里叶变换选项。
9z)p*+r�UK - 在特殊情况下,对于光源模式或探测器而言,
衍射可能无关紧要。 我们将在下面的示例#1和示例#3中讨论这种情况。
A�1`y_
Aj "/�v{B?~%! 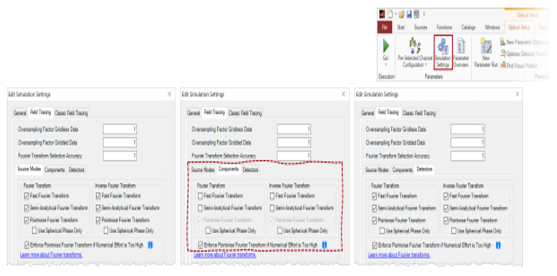 |�FK�##�8� 8I�o-�-Ew3 6. 特殊情况 -X#Zn>#��� 5(F @K�eH> E3X�6-�J|
|�FK�##�8� 8I�o-�-Ew3 6. 特殊情况 -X#Zn>#��� 5(F @K�eH> E3X�6-�J| 多表面元件
^��,��`�;x - 对下列情况应当特别考虑
x��|�
jBn} •透镜系统元件
pJ��*��x[y •球面
透镜元件
0"q�^`�@sZ - 此类组件可以理解为
�JV�O,@~~� •一组曲面元件,以及
L~n�VoKY*V •之间有一些自由空间
L8"0o 0�-� - 傅立叶变换选项也会影响介于两者之间的自由空间传播。
nqX)+{wAXe �UOT�M>d1P 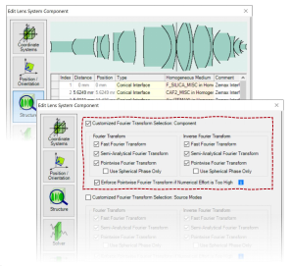 \-A=??��@H k)+2+h�X&>
\-A=??��@H k)+2+h�X&> 在k域的元件
�Z�Ms$C3�� - 当元件的求解器/函数在k域中工作时,傅立叶逆变换选项不会产生任何影响
,�dhSc<:LT - 这适用于以下情况
�)%e`�SGmp •平面表面元件
l���#!p�?l •分层介质元件
+�S!gS|8�P •光栅元件
�ESdjDg$[u •功能
光栅元件
#3��!l6��] /Yk4%ZJ�{ 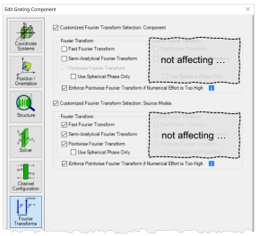 �E .2�b@� la�VqI|0�q 实例#1:低菲涅尔数系统中的针孔 *_�Y{wNF�* �`��Mj>t(�
�E .2�b@� la�VqI|0�q 实例#1:低菲涅尔数系统中的针孔 *_�Y{wNF�* �`��Mj>t(� 1. 实例#1:
成像的光源模式
�:xd�l I`S `?W��y;5-�  n�t$��V��H 7G��N>o@�t ���.L;M-`^ 2. 实例#1:系统内部包含的衍射效应 i"eUacBz/- MX��y�~kb&
n�t$��V��H 7G��N>o@�t ���.L;M-`^ 2. 实例#1:系统内部包含的衍射效应 i"eUacBz/- MX��y�~kb& 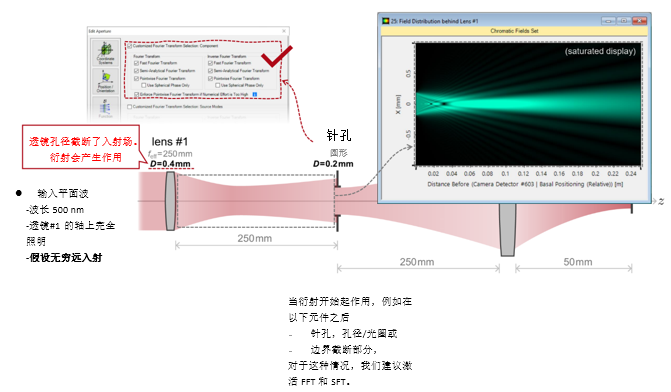 y7[D�9ZvZ
y7[D�9ZvZ 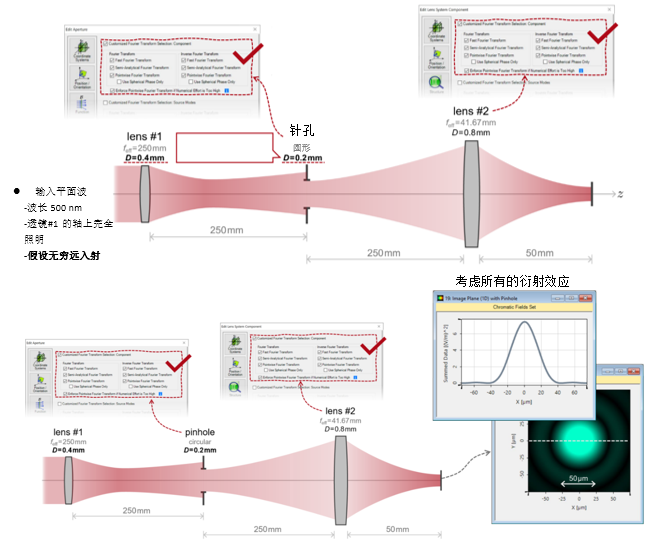 3C�8cvi[IS mj\]oWS7�d 3. 实例#1:出瞳衍射法 S�!*wK���- BEn,�p��y7
3C�8cvi[IS mj\]oWS7�d 3. 实例#1:出瞳衍射法 S�!*wK���- BEn,�p��y7 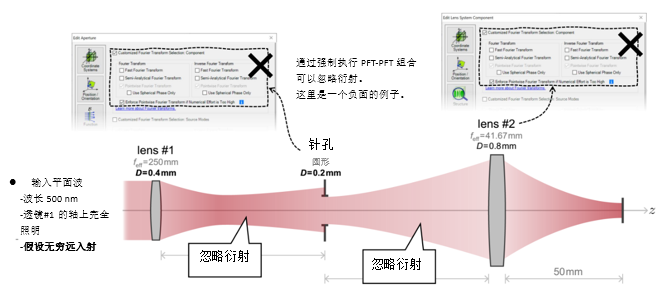 [l;9](\8�O
[l;9](\8�O 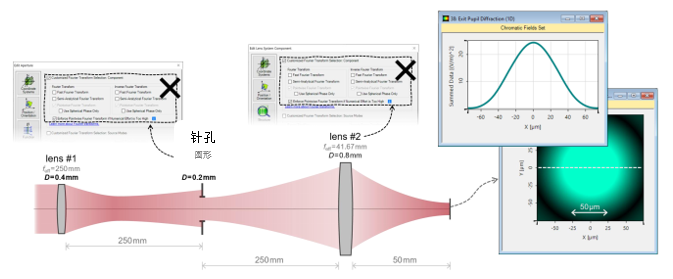 i9�KQp�WG: 4. 实例#1:出瞳衍射与对比 S.,o�m;`� !�JZ)6mtlr
i9�KQp�WG: 4. 实例#1:出瞳衍射与对比 S.,o�m;`� !�JZ)6mtlr 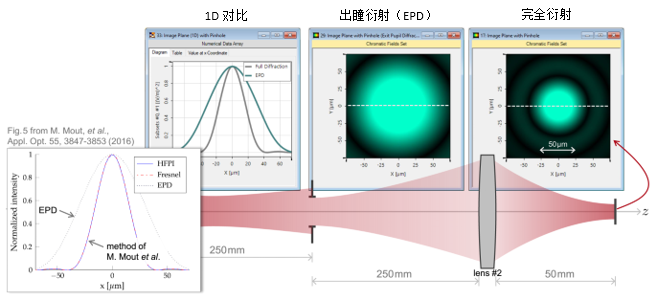 (of�=hzT^? �N�7/e��F9 实例#2:用于激光导星的无焦系统 ��s� zg�q7 ���udCu�m4 1. 实例#2:包含所有可能的衍射 yXg #�<H6V
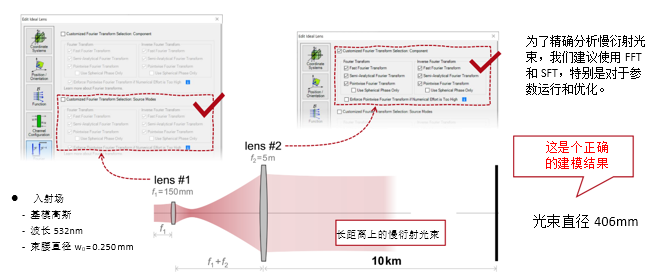
(of�=hzT^? �N�7/e��F9 实例#2:用于激光导星的无焦系统 ��s� zg�q7 ���udCu�m4 1. 实例#2:包含所有可能的衍射 yXg #�<H6V
�-oSfp23�u
 �Qx$C���oY 4�~;x(e@�S x�l.�iI$P 2. 实例#2:忽略透镜间的衍射效应 x'U�v;m�Go ZHQa}�C+
�Qx$C���oY 4�~;x(e@�S x�l.�iI$P 2. 实例#2:忽略透镜间的衍射效应 x'U�v;m�Go ZHQa}�C+ 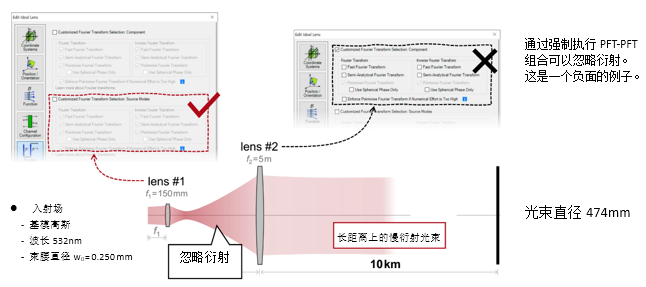 2���<1�8�j `/WX�!4eR, 实例#3:剪切干涉法的准直测试 $w,&h:�.p� d�9'�gH#f? 1. 例#3:刻意忽略衍射 P)Vys�Yb?� $+#Lq.�3,�
2���<1�8�j `/WX�!4eR, 实例#3:剪切干涉法的准直测试 $w,&h:�.p� d�9'�gH#f? 1. 例#3:刻意忽略衍射 P)Vys�Yb?� $+#Lq.�3,� 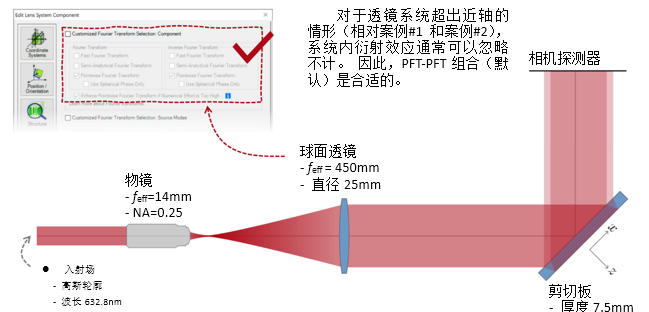 >Q1�59�q�Z ZM:!L�kK�� tS1�(.CRk�
>Q1�59�q�Z ZM:!L�kK�� tS1�(.CRk�
B]):$#{Rxl
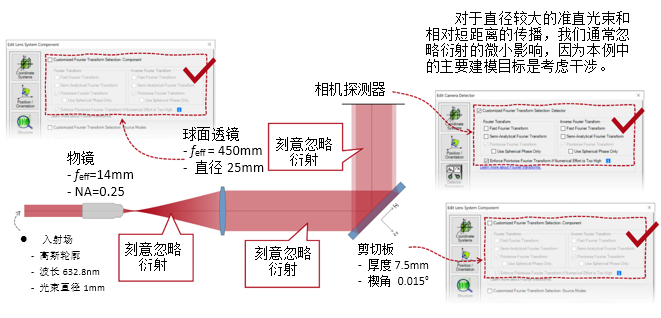 -ti
nL�(?3
-ti
nL�(?3 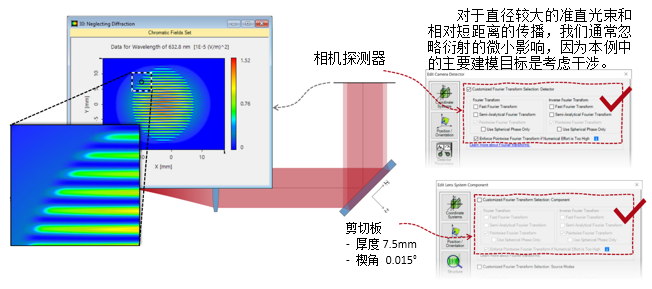 nYf�Z[Q>�v 2. 实例#3:包含衍射 #0yU
K5�J �x3�dP`<
�
nYf�Z[Q>�v 2. 实例#3:包含衍射 #0yU
K5�J �x3�dP`<
� 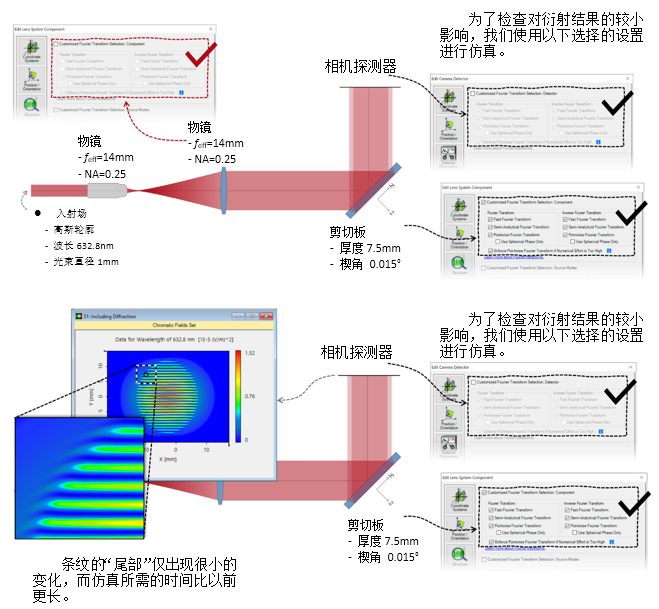 :�C%�cnU;N
:�C%�cnU;N