VirtualLab Fusion包含了多种场求解器和函数。它们可以在空间(x)域或空间频率(k)域工作。为了将不同的求解器和函数简建立连接,实现复杂
系统的建模,x域和k域之间的转换是至关重要的一步。 在本文中,我们将通过不同
实例的讨论来示范如何对VirtualLab Fusion中有三种傅里叶变换算法进行设置。
��XO8 H] U:T5o��]P<  k�[^}ld[�� [1�[[$ Dr� 2. 三种傅里叶变换 8B% O%*5`� 7l�BQ�d�(� mF$j�C�:Tb
k�[^}ld[�� [1�[[$ Dr� 2. 三种傅里叶变换 8B% O%*5`� 7l�BQ�d�(� mF$j�C�:Tb 快速傅里叶变换(FFT)
F�g}��5V�, - 对于不同数值计算,一种
标准而高效的算法。
;d'��O.�i= 半解析傅里叶变换(SFT)
6:7:NI��l: - 一种无需近似的高效重构。
n"Z�,-./�m - 二次相的解析处理,类似chirp-z变换。
� �n�d*!`P dBi3�ZC�AF 逐点傅里叶变换(PSF)
O#��89M�%� - 受静态相位理论启发的一种近似方法,但采用纯粹的数学形式来表达。
_dRn0<#1(k - 对强波前相位是一种高效而精准的方法。
.k?hb]2N ]�#Z$jq{�, z|4@n�qqX�  ybuSqFy`$� mc[�_�>�[m 3. 每个元件的设置 E6KBpQcd[� 'yAo�Z P\| ;�7�hX0�AK
ybuSqFy`$� mc[�_�>�[m 3. 每个元件的设置 E6KBpQcd[� 'yAo�Z P\| ;�7�hX0�AK 傅立叶变换设置
l{7Dv1�[Ss - 对于每个元件和
探测器,都可以使用 “傅立叶变换”选项卡。
{)dEO0� �p - VirtualLab Fusion自动选择所有激活的傅立叶变换选项;不选择未激活的选项。
nms<6�kfzL - 傅立叶变换的组合影响自由空间中向前传播过程的建模。(这意味着不仅适用于元件前面的自由空间——它也适用于具有复杂通道配置的情况)
�e"&�9G}.f 5qAE9G!�c� 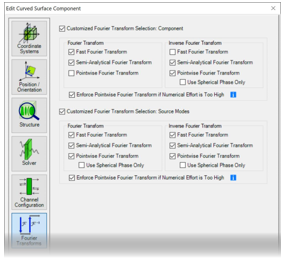 �kgI.k�T(= �&@.=�)4Y� 4. 每个元件的设置 Z_ �FL�=S\ t$kf'�An}/
�kgI.k�T(= �&@.=�)4Y� 4. 每个元件的设置 Z_ �FL�=S\ t$kf'�An}/ 傅里叶变换设置
)]e �d;V�� V,�*�0<�7h 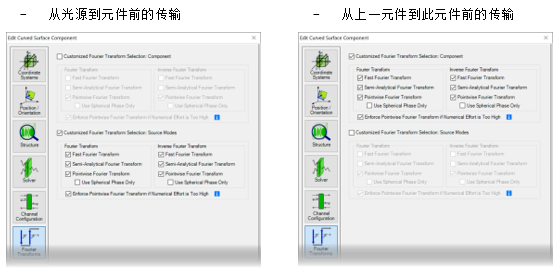 5)�z�j){wL <45dy5!�Tz 5. 默认的傅里叶变换设置 j2v[-N4 {J �'�\vmfp�= �t1_y1!u�Q
5)�z�j){wL <45dy5!�Tz 5. 默认的傅里叶变换设置 j2v[-N4 {J �'�\vmfp�= �t1_y1!u�Q
光源模式和探测器的设置
��"%�@=?X8 - 对于光源模式和探测器,默认情况下将激活所有三个傅里叶变换选项。
C
Wl9�5��g - 在特殊情况下,对于光源模式或探测器而言,
衍射可能无关紧要。 我们将在下面的示例#1和示例#3中讨论这种情况。
07��WI�a@Q QH��?�2v 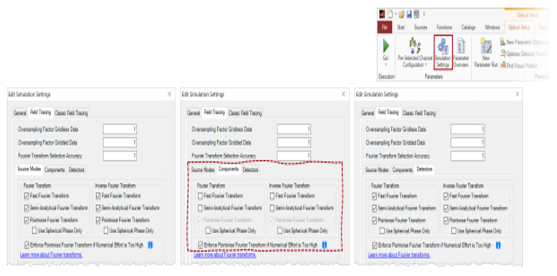 W��a��Z@�� tS.�b5�$Q� 6. 特殊情况 J*4_|j;Z-E d=u%"3��6y Gp�p}Jpj �
W��a��Z@�� tS.�b5�$Q� 6. 特殊情况 J*4_|j;Z-E d=u%"3��6y Gp�p}Jpj � 多表面元件
�sOtN�d({� - 对下列情况应当特别考虑
)<��&�CnK� •透镜系统元件
d�UVT�Q18F •球面
透镜元件
/JY ph^3][ - 此类组件可以理解为
?ia[�KLt�" •一组曲面元件,以及
\#*;�H|U.x •之间有一些自由空间
�-,C�ndRKx - 傅立叶变换选项也会影响介于两者之间的自由空间传播。
Jj _+YfIM� �L0�8���;z 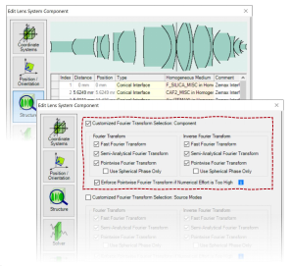 L��Yo�7?rp >Iy��dXmTy
L��Yo�7?rp >Iy��dXmTy 在k域的元件
�ofh�Z�@�3 - 当元件的求解器/函数在k域中工作时,傅立叶逆变换选项不会产生任何影响
.6-o?=5��� - 这适用于以下情况
_(�A��+_| •平面表面元件
O%h
97^�%k •分层介质元件
$ax%K?MB�D •光栅元件
�cL�k+( dn •功能
光栅元件
�RB�ojT� � �sn-+F%��[ 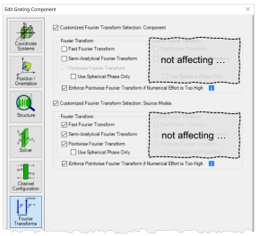 (Y@|h��%1W G5@fq�h6ws 实例#1:低菲涅尔数系统中的针孔 4�F��c1��' vWU4ZB�T8G
(Y@|h��%1W G5@fq�h6ws 实例#1:低菲涅尔数系统中的针孔 4�F��c1��' vWU4ZB�T8G 1. 实例#1:
成像的光源模式
N`�GwL
aF �vT�<wd�#�  4�]N�r�$FY 38S&7>0@|q J_br%A�G<p 2. 实例#1:系统内部包含的衍射效应 ��5v-;*��� ��#a>!U'1|
4�]N�r�$FY 38S&7>0@|q J_br%A�G<p 2. 实例#1:系统内部包含的衍射效应 ��5v-;*��� ��#a>!U'1| 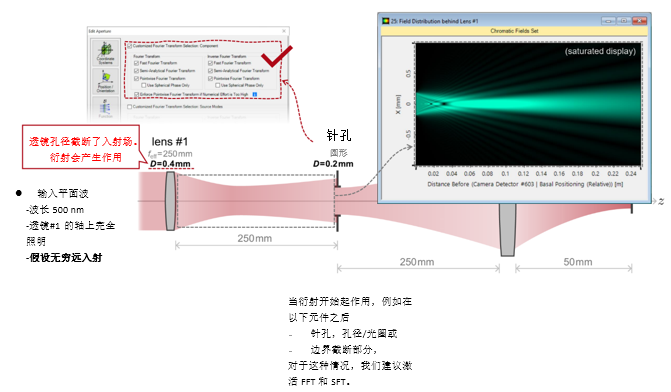 >qGR^�yv�b
>qGR^�yv�b 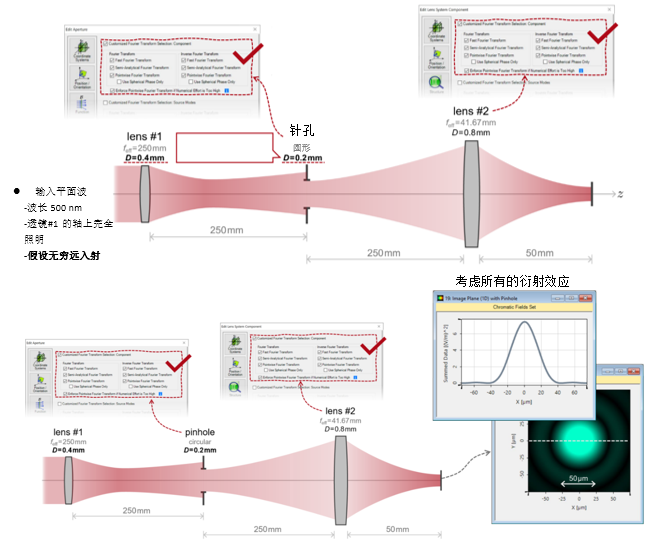 wI]>0geb* :s9�85sE�v 3. 实例#1:出瞳衍射法 #)eJ�z1��~ 0�'2{�[�xF
wI]>0geb* :s9�85sE�v 3. 实例#1:出瞳衍射法 #)eJ�z1��~ 0�'2{�[�xF 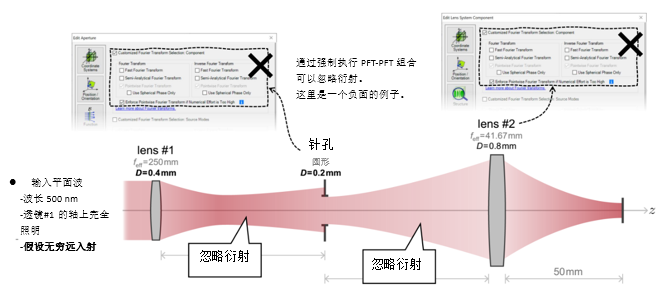 X{5�D�PhB,
X{5�D�PhB, 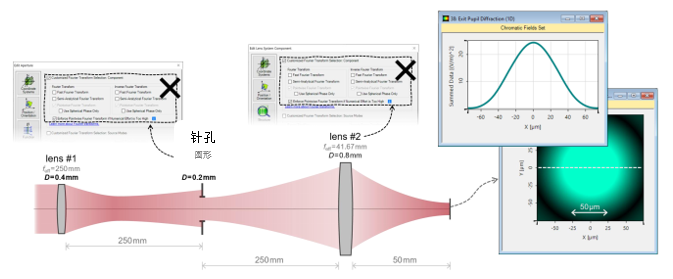 ��>�<�[�.� 4. 实例#1:出瞳衍射与对比 `�-`iS�?� %l�� P� �
��>�<�[�.� 4. 实例#1:出瞳衍射与对比 `�-`iS�?� %l�� P� � 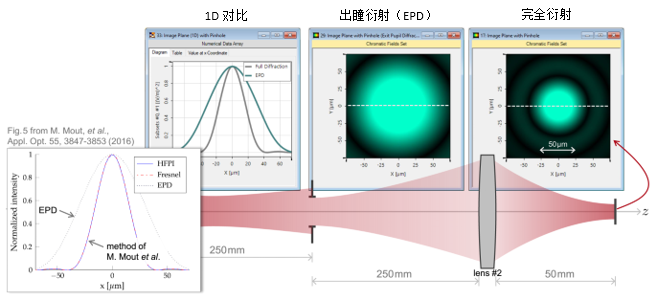 bM_�(`]&*� Z�pBH;{�., 实例#2:用于激光导星的无焦系统 6��_
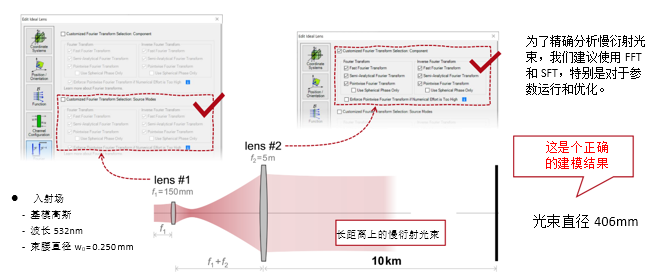
0�w> b4OR�`dd*J 1. 实例#2:包含所有可能的衍射 .
�zMM86�c
bM_�(`]&*� Z�pBH;{�., 实例#2:用于激光导星的无焦系统 6��_
0�w> b4OR�`dd*J 1. 实例#2:包含所有可能的衍射 .
�zMM86�c
q`�K-T�_<�
 Kt7��x'�5� �&x5�ZEe�4 s3%8W==rBW 2. 实例#2:忽略透镜间的衍射效应 ���`l��OoT V� zx(�J)�
Kt7��x'�5� �&x5�ZEe�4 s3%8W==rBW 2. 实例#2:忽略透镜间的衍射效应 ���`l��OoT V� zx(�J)� 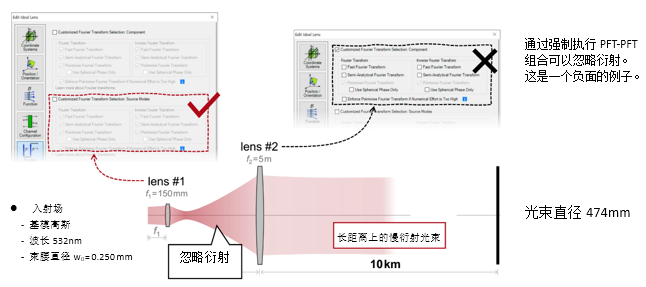 ���b-�/x�� =_:L�
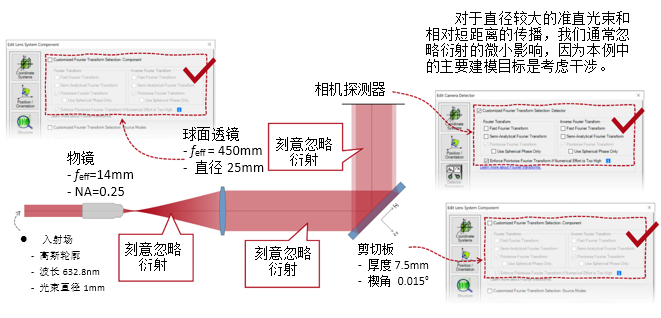
wmI� 实例#3:剪切干涉法的准直测试 ��jmNj#R@t 7�a�np�z%� 1. 例#3:刻意忽略衍射 :�QSW���^x ty�=?S�ZF�
���b-�/x�� =_:L�
wmI� 实例#3:剪切干涉法的准直测试 ��jmNj#R@t 7�a�np�z%� 1. 例#3:刻意忽略衍射 :�QSW���^x ty�=?S�ZF� 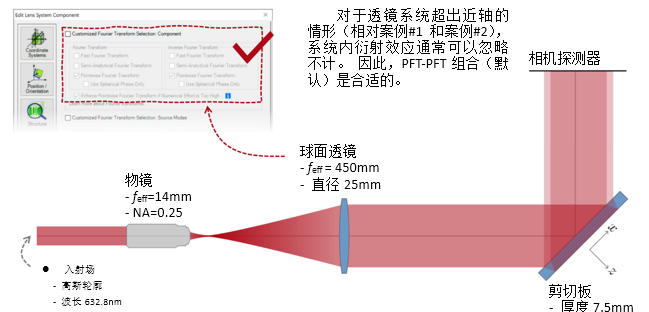 [|Pe'?z�kf +�Y[+2=�lO +W4g:b�B1�
[|Pe'?z�kf +�Y[+2=�lO +W4g:b�B1�
6b)U�oJx�j
 BC[d={�_-�
BC[d={�_-� 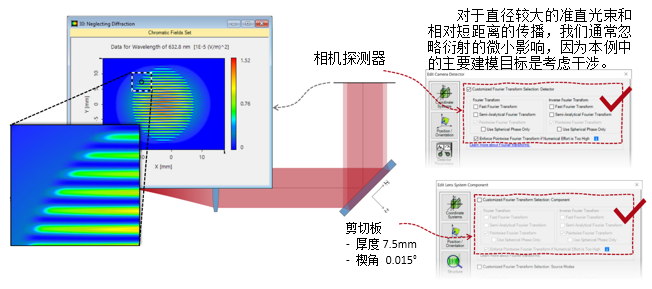 Vb�#@o�)�z 2. 实例#3:包含衍射 �*\vc_N�P] E�qlu�xD=
Vb�#@o�)�z 2. 实例#3:包含衍射 �*\vc_N�P] E�qlu�xD= 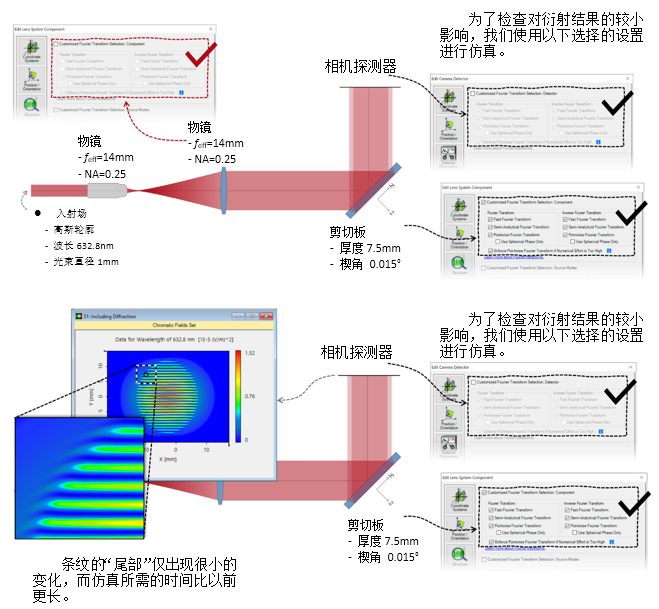 <L��Zvh�8�
<L��Zvh�8�