VirtualLab Fusion包含了多种场求解器和函数。它们可以在空间(x)域或空间频率(k)域工作。为了将不同的求解器和函数简建立连接,实现复杂
系统的建模,x域和k域之间的转换是至关重要的一步。 在本文中,我们将通过不同
实例的讨论来示范如何对VirtualLab Fusion中有三种傅里叶变换算法进行设置。
NzP5s&,C69 �C��6�XZZ�  |Ir&C[QS{y Y_}DF.>I P 2. 三种傅里叶变换 �Z�\�`�i�~ 5�V^+�;�eO PJCRvs��|X
|Ir&C[QS{y Y_}DF.>I P 2. 三种傅里叶变换 �Z�\�`�i�~ 5�V^+�;�eO PJCRvs��|X 快速傅里叶变换(FFT)
f��[b�x|6� - 对于不同数值计算,一种
标准而高效的算法。
�ezC�2E/#� 半解析傅里叶变换(SFT)
3%JPJ�uNVw - 一种无需近似的高效重构。
XA$Z�7_gu3 - 二次相的解析处理,类似chirp-z变换。
2
P=c�1��; *)2&�gQ&%+ 逐点傅里叶变换(PSF)
G%V*+On�d - 受静态相位理论启发的一种近似方法,但采用纯粹的数学形式来表达。
�2[Ja|W\If - 对强波前相位是一种高效而精准的方法。
�"s�6O|=^* ��^_��c�R� GV5hm�DzRs  � -<'�&�"- #Zm��%U_$< 3. 每个元件的设置 AvN\^
��&G (��o�YM}#Q 1i�.t�^�PY
� -<'�&�"- #Zm��%U_$< 3. 每个元件的设置 AvN\^
��&G (��o�YM}#Q 1i�.t�^�PY 傅立叶变换设置
C>�?`�1d@� - 对于每个元件和
探测器,都可以使用 “傅立叶变换”选项卡。
�6�n��
2LG - VirtualLab Fusion自动选择所有激活的傅立叶变换选项;不选择未激活的选项。
7%-+7O�3ud - 傅立叶变换的组合影响自由空间中向前传播过程的建模。(这意味着不仅适用于元件前面的自由空间——它也适用于具有复杂通道配置的情况)
�<Q4y�N!6� b�Oi`JJ^�� 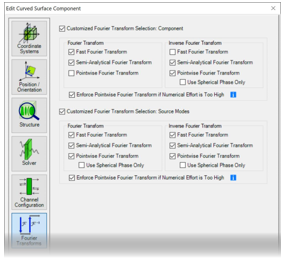 &��s|&��cT Z"# /,?|3@ 4. 每个元件的设置 ;n9r;$!f�� oW�Z�bfR9R
&��s|&��cT Z"# /,?|3@ 4. 每个元件的设置 ;n9r;$!f�� oW�Z�bfR9R 傅里叶变换设置
b��Gl5�=`� ?�E@�9�Nvr 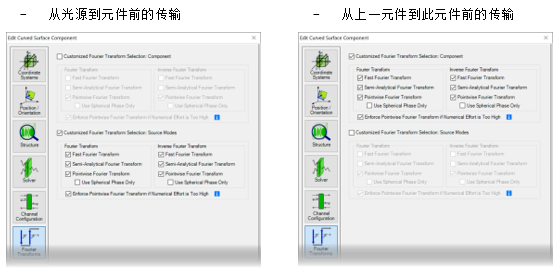 *u�Llf'qU] O;N�QJ$^bI 5. 默认的傅里叶变换设置 gC�Mwma�nX ��Cy�w��Q ��Kh!h��_�
*u�Llf'qU] O;N�QJ$^bI 5. 默认的傅里叶变换设置 gC�Mwma�nX ��Cy�w��Q ��Kh!h��_�
光源模式和探测器的设置
uKI2KWU?2 - 对于光源模式和探测器,默认情况下将激活所有三个傅里叶变换选项。
�mgB�7l0)b - 在特殊情况下,对于光源模式或探测器而言,
衍射可能无关紧要。 我们将在下面的示例#1和示例#3中讨论这种情况。
QT;mCD=O�D �v.08,P�{b 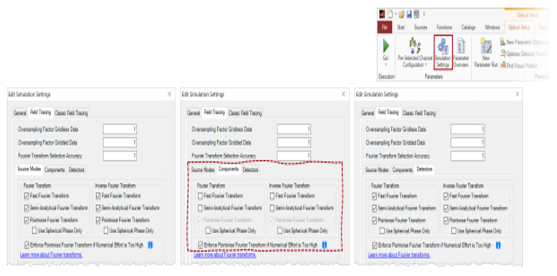 _�$+lyea � a8#6�}`|C? 6. 特殊情况 *g}(q��jl< �RtrE�SwtR PKT/U^�2X]
_�$+lyea � a8#6�}`|C? 6. 特殊情况 *g}(q��jl< �RtrE�SwtR PKT/U^�2X] 多表面元件
��::�\��7s - 对下列情况应当特别考虑
�B�u ~N�)^ •透镜系统元件
7�>g^O�E f •球面
透镜元件
�X]?�qn�s7 - 此类组件可以理解为
vGK'U*gGD� •一组曲面元件,以及
�(f^K\�7HM •之间有一些自由空间
� xZ*.@Pkr - 傅立叶变换选项也会影响介于两者之间的自由空间传播。
�?l�h
`>v� ?mK`W�leh? 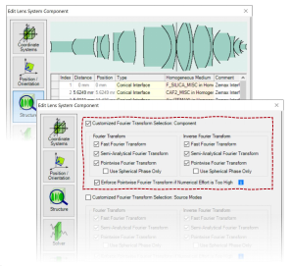 \\F@_nB�,b !+?,�y/*5(
\\F@_nB�,b !+?,�y/*5( 在k域的元件
O\64�)V�
0 - 当元件的求解器/函数在k域中工作时,傅立叶逆变换选项不会产生任何影响
,8KD-"�l^g - 这适用于以下情况
: -�@o3Syg •平面表面元件
�V�@0Z�\�& •分层介质元件
x��"�@Y�[� •光栅元件
%)�7HBj(*J •功能
光栅元件
;:nO5VF�Og N�79��8("� 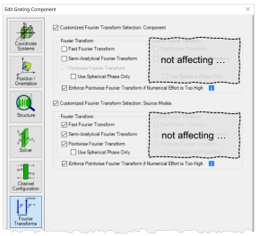 SBn�wlM"AN /( /)nYAjk 实例#1:低菲涅尔数系统中的针孔 e}u#�:ysj� kI>Iq
Q-h
SBn�wlM"AN /( /)nYAjk 实例#1:低菲涅尔数系统中的针孔 e}u#�:ysj� kI>Iq
Q-h 1. 实例#1:
成像的光源模式
n�VqFCB�B� 6�9U�[�kW&  -[��cl]H)V j��P{LMm�V ��9/��rX%� 2. 实例#1:系统内部包含的衍射效应 tL?��nO#Qx *5DO�TWos�
-[��cl]H)V j��P{LMm�V ��9/��rX%� 2. 实例#1:系统内部包含的衍射效应 tL?��nO#Qx *5DO�TWos� 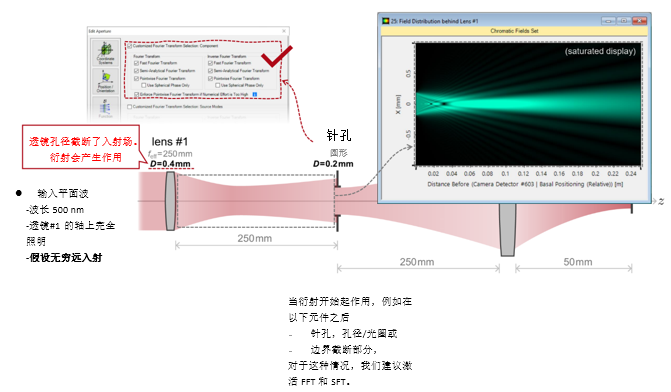 mK3U*)�A
�
mK3U*)�A
� 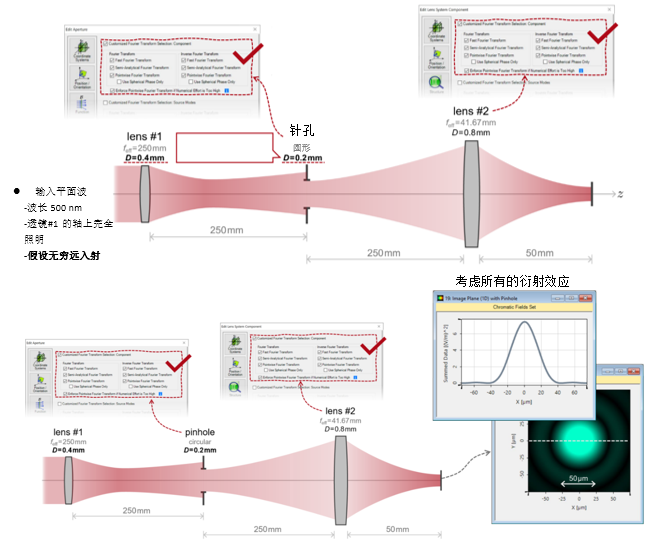 7�l"N%���e C�d:ofv/3� 3. 实例#1:出瞳衍射法 �H7 a�cT� �V9��:h�4]
7�l"N%���e C�d:ofv/3� 3. 实例#1:出瞳衍射法 �H7 a�cT� �V9��:h�4] 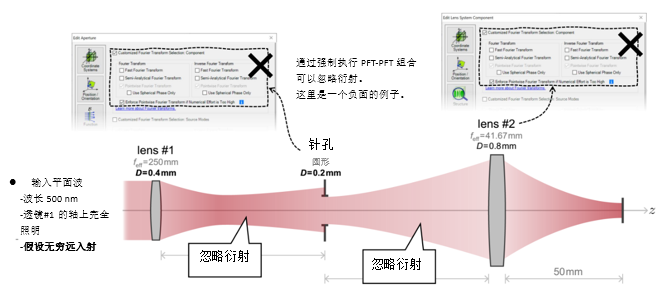 \;w+_<zE5{
\;w+_<zE5{ 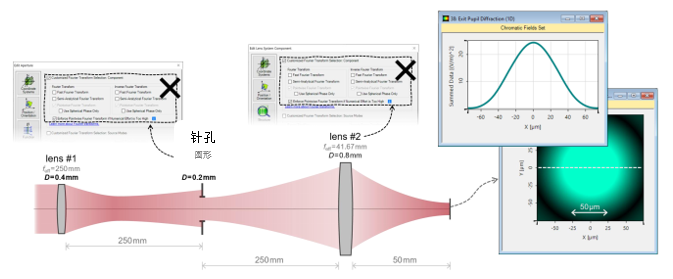 hadGF%> O6 4. 实例#1:出瞳衍射与对比 <<@vy{*�Hg ��T&_!�AjH
hadGF%> O6 4. 实例#1:出瞳衍射与对比 <<@vy{*�Hg ��T&_!�AjH 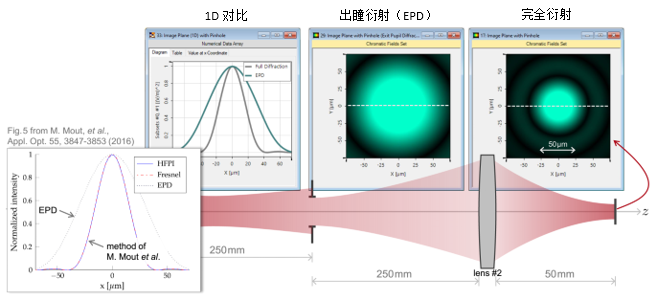 &J~vXk:
!� [���KIK}: 实例#2:用于激光导星的无焦系统 4%Q8>mE�vT ��;~�Eb Q� 1. 实例#2:包含所有可能的衍射 �V j\1��HQ
&J~vXk:
!� [���KIK}: 实例#2:用于激光导星的无焦系统 4%Q8>mE�vT ��;~�Eb Q� 1. 实例#2:包含所有可能的衍射 �V j\1��HQ
|U�z�?�i7z
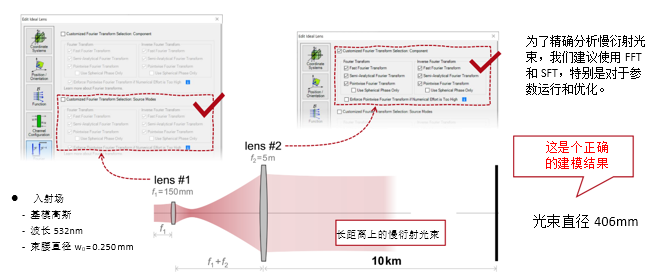 ;<�D�o�u7= :IF�Tiq5a; �6Sh0�%F�s 2. 实例#2:忽略透镜间的衍射效应 n>F1G�
�MX Las�4ux[_�
;<�D�o�u7= :IF�Tiq5a; �6Sh0�%F�s 2. 实例#2:忽略透镜间的衍射效应 n>F1G�
�MX Las�4ux[_� 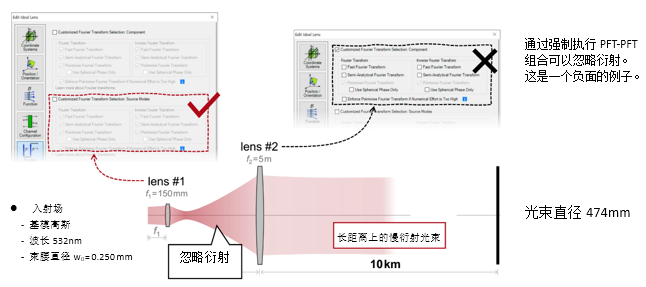 #�4. S2m4� �zmf`�}j[� 实例#3:剪切干涉法的准直测试 wv>u�T{g# kr�kRP�%jy 1. 例#3:刻意忽略衍射 3%J�g' Tr+ S$�q:hXZ#e
#�4. S2m4� �zmf`�}j[� 实例#3:剪切干涉法的准直测试 wv>u�T{g# kr�kRP�%jy 1. 例#3:刻意忽略衍射 3%J�g' Tr+ S$�q:hXZ#e 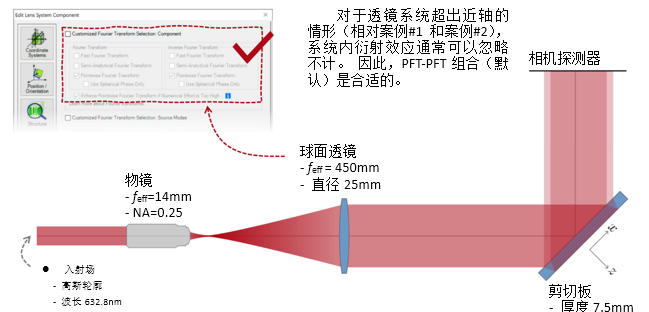 \BC|�`�)0h k'u��N2�m c��yq��]-B
\BC|�`�)0h k'u��N2�m c��yq��]-B
.Yqu�OCc�(
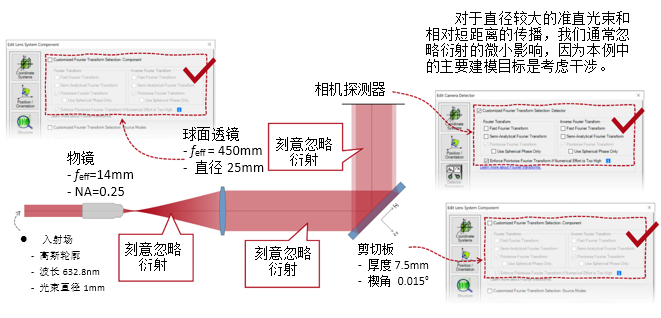 �}�
F�cWzi
�}�
F�cWzi 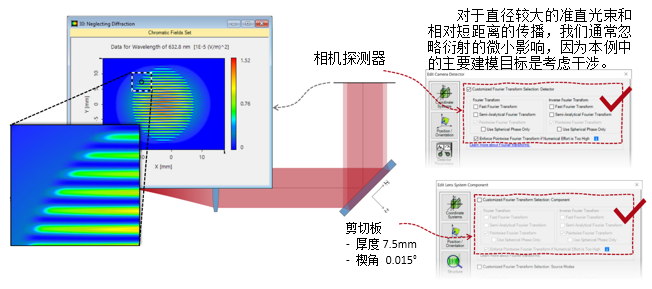 B mq7w�,L. 2. 实例#3:包含衍射 a��g�*R�Q� PJ�u)%al��
B mq7w�,L. 2. 实例#3:包含衍射 a��g�*R�Q� PJ�u)%al�� 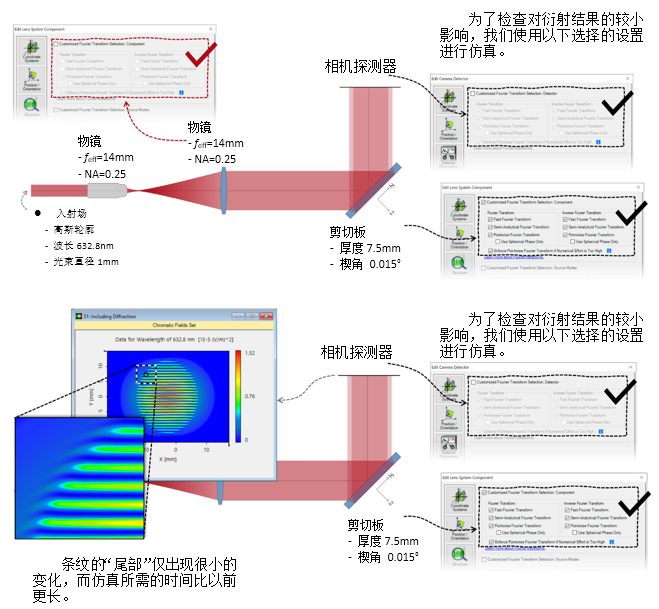 {6Y�LiQ�*_
{6Y�LiQ�*_