VirtualLab Fusion包含了多种场求解器和函数。它们可以在空间(x)域或空间频率(k)域工作。为了将不同的求解器和函数简建立连接,实现复杂
系统的建模,x域和k域之间的转换是至关重要的一步。 在本文中,我们将通过不同
实例的讨论来示范如何对VirtualLab Fusion中有三种傅里叶变换算法进行设置。
5@CpP-W#�� \/�X{n*Hw?  Y)5)s0�} � U"/y�B8!W� 2. 三种傅里叶变换 �\&# p1K(H Z�tKQ]jV&@ A�&;EV#]ge
Y)5)s0�} � U"/y�B8!W� 2. 三种傅里叶变换 �\&# p1K(H Z�tKQ]jV&@ A�&;EV#]ge 快速傅里叶变换(FFT)
�Iy6p�>z�| - 对于不同数值计算,一种
标准而高效的算法。
}^IwQm*�i� 半解析傅里叶变换(SFT)
*u<r�U�,C8 - 一种无需近似的高效重构。
�%�zRiLcAT - 二次相的解析处理,类似chirp-z变换。
*EX$v�4BX =��]WW'~�� 逐点傅里叶变换(PSF)
�.wM:YX'[G - 受静态相位理论启发的一种近似方法,但采用纯粹的数学形式来表达。
+$(7��1#'y - 对强波前相位是一种高效而精准的方法。
(�v|i�xa� C��L
EpB2_ �zZ<ns+�h  ?�'�TA!�MR XX*'�N�+�� 3. 每个元件的设置 <[�/PyNYK� |K'Gw�}fX/ B�-B?Ff>��
?�'�TA!�MR XX*'�N�+�� 3. 每个元件的设置 <[�/PyNYK� |K'Gw�}fX/ B�-B?Ff>�� 傅立叶变换设置
�?,D�>+�:: - 对于每个元件和
探测器,都可以使用 “傅立叶变换”选项卡。
s��+(l7xH$ - VirtualLab Fusion自动选择所有激活的傅立叶变换选项;不选择未激活的选项。
:P���j W:] - 傅立叶变换的组合影响自由空间中向前传播过程的建模。(这意味着不仅适用于元件前面的自由空间——它也适用于具有复杂通道配置的情况)
NW��}>pb9 �e~tr^$/�( 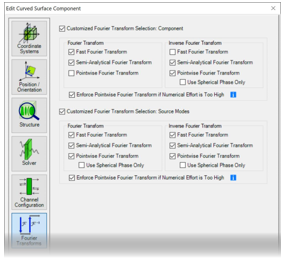 %�H�� 8A=� �ev)�rOcOU 4. 每个元件的设置 ',L{C�QA?c cZ�C�Gnzy
%�H�� 8A=� �ev)�rOcOU 4. 每个元件的设置 ',L{C�QA?c cZ�C�Gnzy 傅里叶变换设置
)RpqZ�e/h4 J�(3gT�}z- 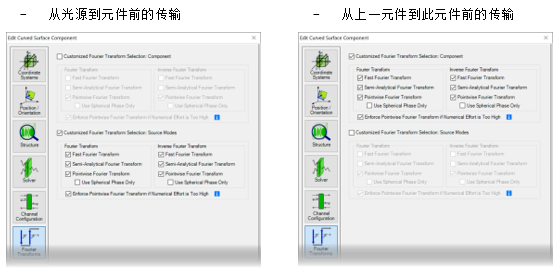 N�vEm�,E\| J�sl��k� 5. 默认的傅里叶变换设置 / c4;3>I�S ���N�8Rm}) =}B��4�I�
N�vEm�,E\| J�sl��k� 5. 默认的傅里叶变换设置 / c4;3>I�S ���N�8Rm}) =}B��4�I�
光源模式和探测器的设置
U�fm(2`�FQ - 对于光源模式和探测器,默认情况下将激活所有三个傅里叶变换选项。
7KvXT�rN!9 - 在特殊情况下,对于光源模式或探测器而言,
衍射可能无关紧要。 我们将在下面的示例#1和示例#3中讨论这种情况。
E.�?E~�}z UY�?�i� E= 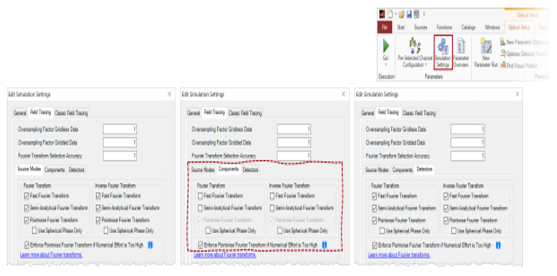 e�{^:/WcYB �[��]�GthF 6. 特殊情况 z Y$�X|=�f 8o*\W�$K@� L?Kz
P.(t+
e�{^:/WcYB �[��]�GthF 6. 特殊情况 z Y$�X|=�f 8o*\W�$K@� L?Kz
P.(t+ 多表面元件
T#MA#H��2� - 对下列情况应当特别考虑
fcgDU *A%� •透镜系统元件
m1~qaD<DZ$ •球面
透镜元件
oG4�w8�+N� - 此类组件可以理解为
�2N8rM}?90 •一组曲面元件,以及
&:���!ZT=� •之间有一些自由空间
t(Q&H!~e
� - 傅立叶变换选项也会影响介于两者之间的自由空间传播。
zbF:R[��) [�u�`17hyX 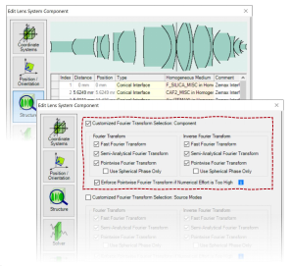 �Ov0�O#�` ~�z�X�G<}n
�Ov0�O#�` ~�z�X�G<}n 在k域的元件
1q��B!RIau - 当元件的求解器/函数在k域中工作时,傅立叶逆变换选项不会产生任何影响
F�g��FJ0fo - 这适用于以下情况
2<46jJYL'� •平面表面元件
WH�pUjyBP� •分层介质元件
��,�7n;|1` •光栅元件
u7�<qaOzs? •功能
光栅元件
��vF*^xh�h xA[W��b��' 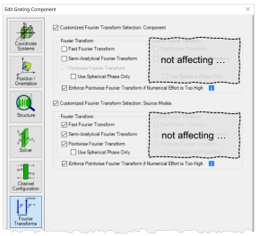 kT Z��?+hx �y�V 9]_�k 实例#1:低菲涅尔数系统中的针孔 ,Z���zB#�\ ST�FQ�";z$
kT Z��?+hx �y�V 9]_�k 实例#1:低菲涅尔数系统中的针孔 ,Z���zB#�\ ST�FQ�";z$ 1. 实例#1:
成像的光源模式
+
d+�hvwEM �4�~M��J4:  l0:e=q2Ax Z1)jRE�2dl QK``tWLIg7 2. 实例#1:系统内部包含的衍射效应 SI�aUr��C� �.N�zW�@�|
l0:e=q2Ax Z1)jRE�2dl QK``tWLIg7 2. 实例#1:系统内部包含的衍射效应 SI�aUr��C� �.N�zW�@�| 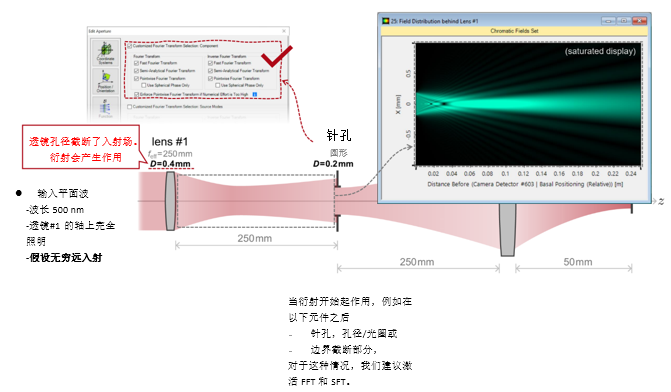 ei��+��9G,
ei��+��9G, 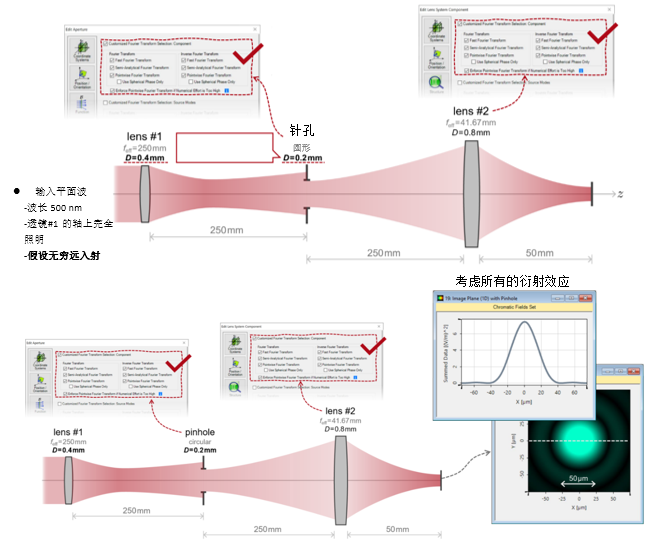 Xh�7~MU~�X %-1BA�*J`| 3. 实例#1:出瞳衍射法 y(bt56 |
z �/e�l[�"l�
Xh�7~MU~�X %-1BA�*J`| 3. 实例#1:出瞳衍射法 y(bt56 |
z �/e�l[�"l� 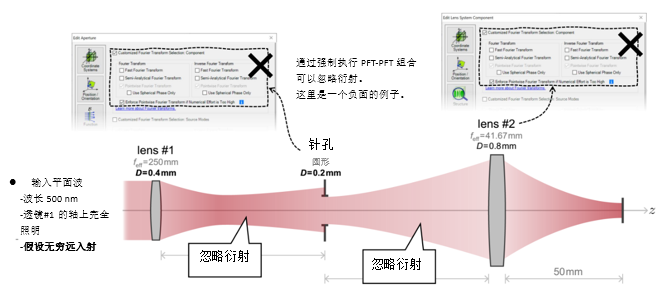 ��a=:{{\1o
��a=:{{\1o 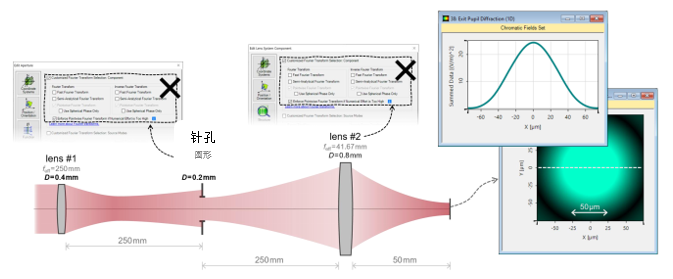 �]<\;d�
B 4. 实例#1:出瞳衍射与对比 #x4h_K
Y�� ]R��J��b�;
�]<\;d�
B 4. 实例#1:出瞳衍射与对比 #x4h_K
Y�� ]R��J��b�; 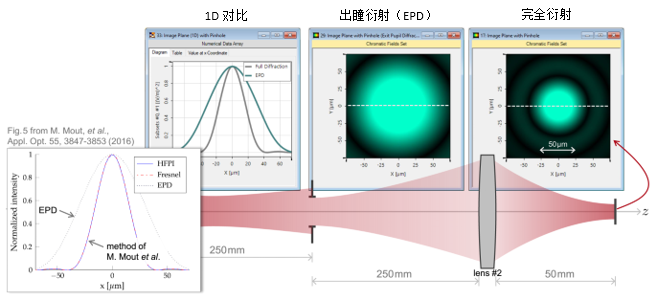 g���|v1qfK +�qh�<
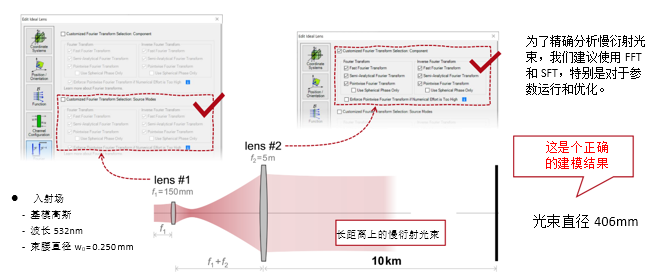
Fj> 实例#2:用于激光导星的无焦系统 ]�]h:�#A�2 -�$L],q_S^ 1. 实例#2:包含所有可能的衍射 (���_i
v�N
g���|v1qfK +�qh�<
Fj> 实例#2:用于激光导星的无焦系统 ]�]h:�#A�2 -�$L],q_S^ 1. 实例#2:包含所有可能的衍射 (���_i
v�N
ABq�{<2iYN
 O�W63^wA`s �N��SxPN:� `l�u"�y��F 2. 实例#2:忽略透镜间的衍射效应 $$bTd��3N+ �(A���]�m=
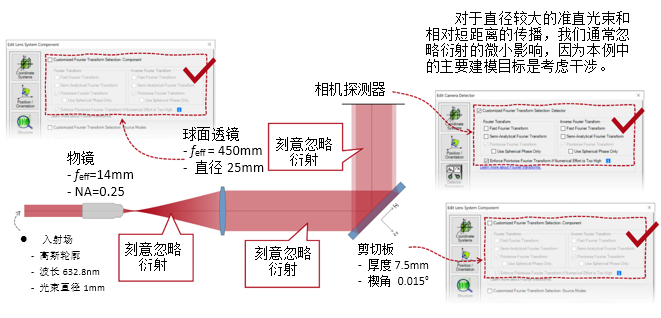
O�W63^wA`s �N��SxPN:� `l�u"�y��F 2. 实例#2:忽略透镜间的衍射效应 $$bTd��3N+ �(A���]�m= 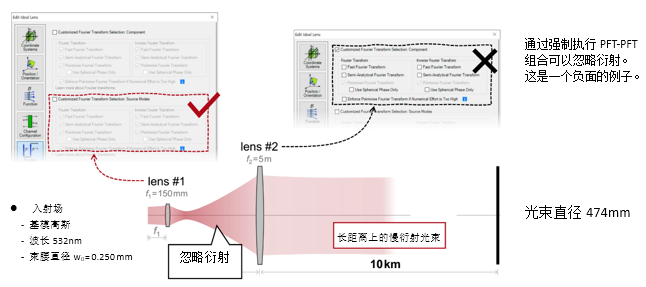 �H/p-�YtY� 'Tru�?�y�\ 实例#3:剪切干涉法的准直测试 �Y�jX!q]56 f'zU�^/$rf 1. 例#3:刻意忽略衍射 #^4�>�U&?� �g�vTO�C�F
�H/p-�YtY� 'Tru�?�y�\ 实例#3:剪切干涉法的准直测试 �Y�jX!q]56 f'zU�^/$rf 1. 例#3:刻意忽略衍射 #^4�>�U&?� �g�vTO�C�F 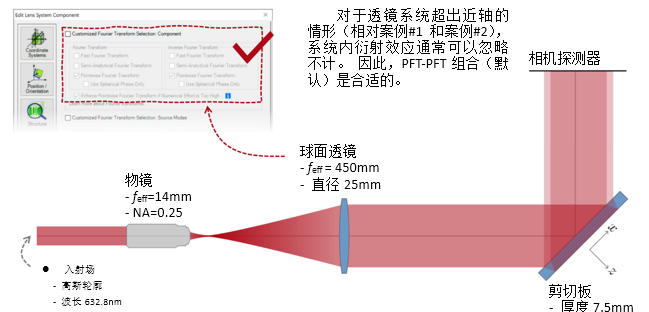 ?sjZ13 SUa v8U1uO�R,% }Pm(oR'KTJ
?sjZ13 SUa v8U1uO�R,% }Pm(oR'KTJ
w�.T�=�Lzp
 qUoMg�%Z%l
qUoMg�%Z%l 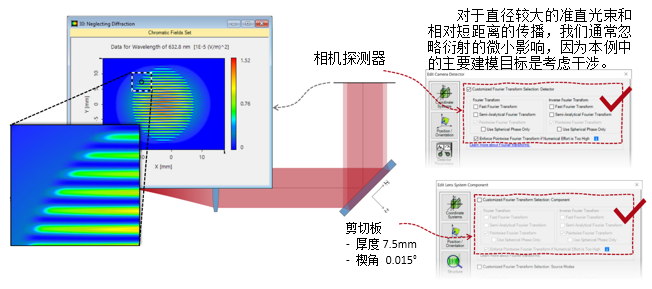 N?2�#�YTjR 2. 实例#3:包含衍射 (IWix)�{�� }!��Diai*C
N?2�#�YTjR 2. 实例#3:包含衍射 (IWix)�{�� }!��Diai*C 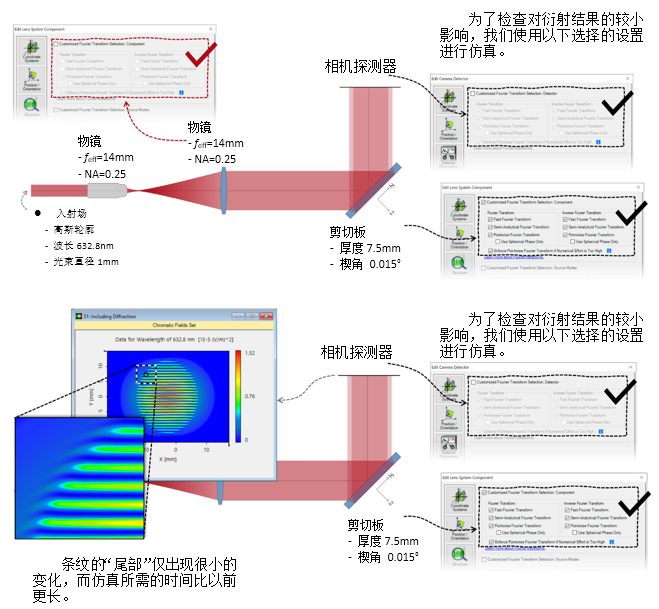 8[`^�(O#\E
8[`^�(O#\E