VirtualLab Fusion包含了多种场求解器和函数。它们可以在空间(x)域或空间频率(k)域工作。为了将不同的求解器和函数简建立连接,实现复杂
系统的建模,x域和k域之间的转换是至关重要的一步。 在本文中,我们将通过不同
实例的讨论来示范如何对VirtualLab Fusion中有三种傅里叶变换算法进行设置。
2,:{ 5�]Q$ (�k�R
NqfX  |m�KohV qr <( �OHX�3~ 2. 三种傅里叶变换 ry|a_3X(I� t*�= nI $� C��<=rnIf'
|m�KohV qr <( �OHX�3~ 2. 三种傅里叶变换 ry|a_3X(I� t*�= nI $� C��<=rnIf' 快速傅里叶变换(FFT)
bit|L�7*14 - 对于不同数值计算,一种
标准而高效的算法。
I\TSVJk^Xi 半解析傅里叶变换(SFT)
IM1&g7Qs2� - 一种无需近似的高效重构。
$��,K@x�q5 - 二次相的解析处理,类似chirp-z变换。
f+9WGN�pw� c@g�(_%_|2 逐点傅里叶变换(PSF)
/�)��kJ iV - 受静态相位理论启发的一种近似方法,但采用纯粹的数学形式来表达。
�og�Iu\kiZ - 对强波前相位是一种高效而精准的方法。
|@_<^cV110 �Li�lK6�K� 5X�r})%��L  VLV]e�_D6s xxs
�+=.2� 3. 每个元件的设置 :�|�9vMM^$ u�D(C jHM> D]_6OlIE#'
VLV]e�_D6s xxs
�+=.2� 3. 每个元件的设置 :�|�9vMM^$ u�D(C jHM> D]_6OlIE#' 傅立叶变换设置
'Y @yW��3K - 对于每个元件和
探测器,都可以使用 “傅立叶变换”选项卡。
hrn�E5=�iY - VirtualLab Fusion自动选择所有激活的傅立叶变换选项;不选择未激活的选项。
S!PG7�h�K2 - 傅立叶变换的组合影响自由空间中向前传播过程的建模。(这意味着不仅适用于元件前面的自由空间——它也适用于具有复杂通道配置的情况)
8KJ`+"�<=@ x:0swZ5�Z 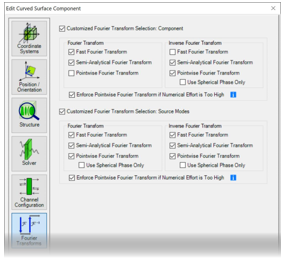 hqln��6m� C!�:Lk,�Z 4. 每个元件的设置 :
j���k��O qe�F�aY74S
hqln��6m� C!�:Lk,�Z 4. 每个元件的设置 :
j���k��O qe�F�aY74S 傅里叶变换设置
�:�rM2G@{ FS�5iUH+5� 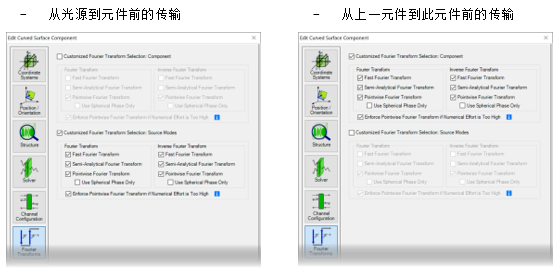 r�rz(�[2E2 a>l,H#w*vW 5. 默认的傅里叶变换设置 wlP3 ��XF? zgz!"knVx� 7 q!==P=��
r�rz(�[2E2 a>l,H#w*vW 5. 默认的傅里叶变换设置 wlP3 ��XF? zgz!"knVx� 7 q!==P=��
光源模式和探测器的设置
O�[�= L#wi - 对于光源模式和探测器,默认情况下将激活所有三个傅里叶变换选项。
+%j27~�R>D - 在特殊情况下,对于光源模式或探测器而言,
衍射可能无关紧要。 我们将在下面的示例#1和示例#3中讨论这种情况。
P>r�RD`Yy\ L+G0/G}O�\ 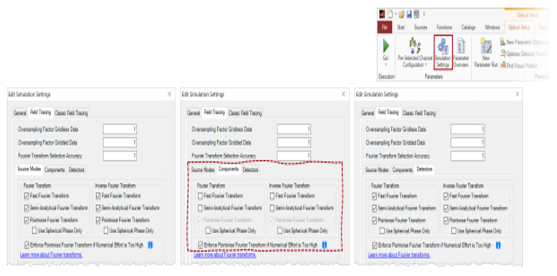 ��omg��#[� !U:�&8��Le 6. 特殊情况 >yKz8�SV#� g4k3~,=�D3 �C9�?mxa*z
��omg��#[� !U:�&8��Le 6. 特殊情况 >yKz8�SV#� g4k3~,=�D3 �C9�?mxa*z 多表面元件
I'BHNZO5tf - 对下列情况应当特别考虑
%\�HE1d5;� •透镜系统元件
ilQ}{�p6I •球面
透镜元件
L7��5�4odc - 此类组件可以理解为
tl� ����/i •一组曲面元件,以及
���HI�{q#� •之间有一些自由空间
�Uhr2"Nuuy - 傅立叶变换选项也会影响介于两者之间的自由空间传播。
0?�oL zw&� ;�=$;h6W�0 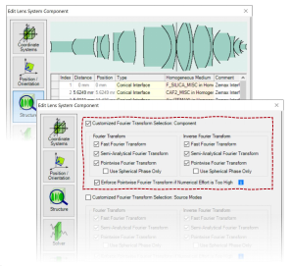 dh�A��~Y�u ,\iXZ5"�R
dh�A��~Y�u ,\iXZ5"�R 在k域的元件
&k,DAx`rN; - 当元件的求解器/函数在k域中工作时,傅立叶逆变换选项不会产生任何影响
pT���GGJ, - 这适用于以下情况
p?#T^{Quz~ •平面表面元件
�C_>Xtc��U •分层介质元件
;^b�fLSWm{ •光栅元件
;��v\s�7y •功能
光栅元件
�IV!`�~\�@ EP�n!6W�5^ 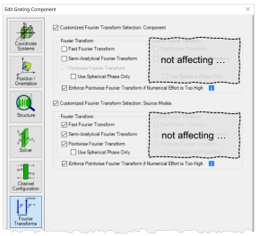 C�R23$<FC� l0�^�cd�l- 实例#1:低菲涅尔数系统中的针孔 z/�"*-+j�� ��f�6K.�F
C�R23$<FC� l0�^�cd�l- 实例#1:低菲涅尔数系统中的针孔 z/�"*-+j�� ��f�6K.�F 1. 实例#1:
成像的光源模式
/0qb�Rk� i �FS=�yc.Q_  T5|kO:CbHq �, @UO�j= 'u��x!:b"� 2. 实例#1:系统内部包含的衍射效应 5P�Z�!Z�O& (_4�D�Z�Mf
T5|kO:CbHq �, @UO�j= 'u��x!:b"� 2. 实例#1:系统内部包含的衍射效应 5P�Z�!Z�O& (_4�D�Z�Mf 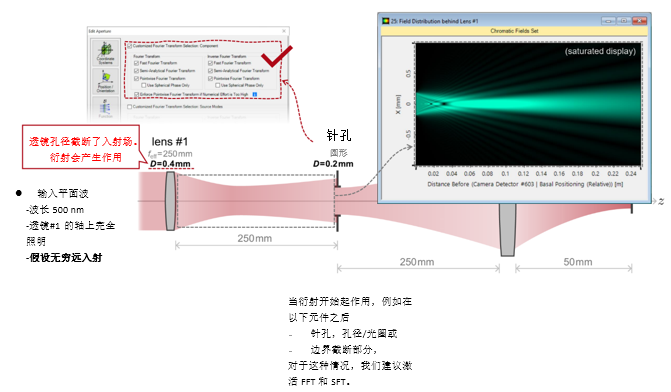 �_p4]\�L�A
�_p4]\�L�A 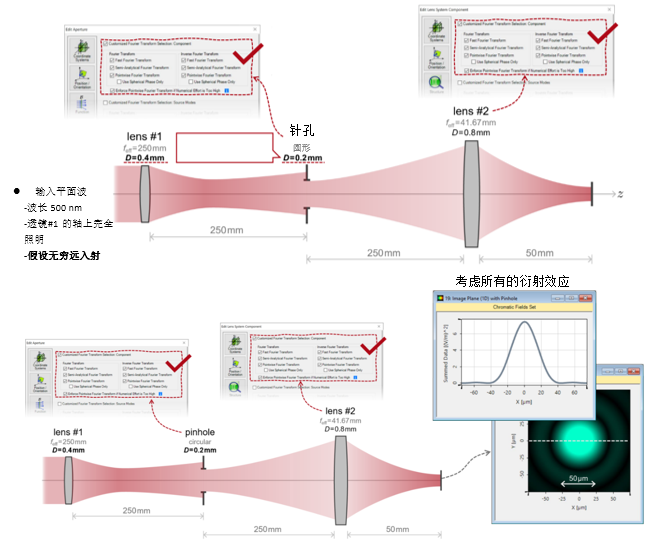 �}\S'oC\�[ Cp/f1�8zO� 3. 实例#1:出瞳衍射法 ��Uc:N�W
� ~I��W{^u��
�}\S'oC\�[ Cp/f1�8zO� 3. 实例#1:出瞳衍射法 ��Uc:N�W
� ~I��W{^u�� 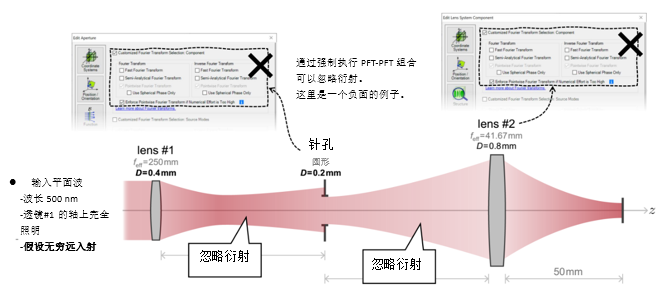 O<Q8%�Az��
O<Q8%�Az�� 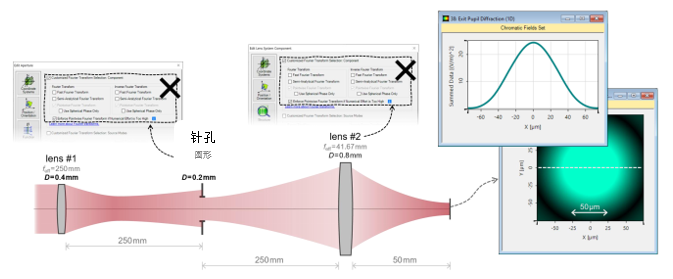 r!f���UMDS 4. 实例#1:出瞳衍射与对比 ��'4{=�x]K m�-azd�~r[
r!f���UMDS 4. 实例#1:出瞳衍射与对比 ��'4{=�x]K m�-azd�~r[ 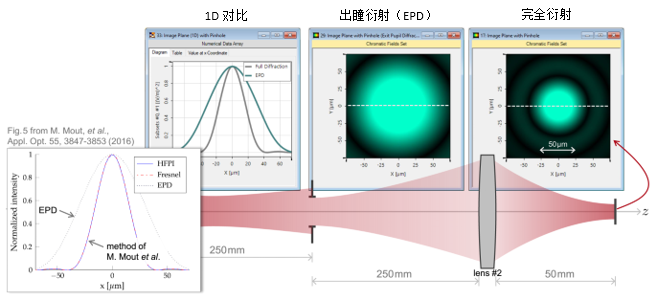 Dq~�;h \=' �N��jZ~b/ 实例#2:用于激光导星的无焦系统 NW5OLa")J< ;6``t+]q
� 1. 实例#2:包含所有可能的衍射 2<B'PR-??y
Dq~�;h \=' �N��jZ~b/ 实例#2:用于激光导星的无焦系统 NW5OLa")J< ;6``t+]q
� 1. 实例#2:包含所有可能的衍射 2<B'PR-??y
3%�5�YU�G@
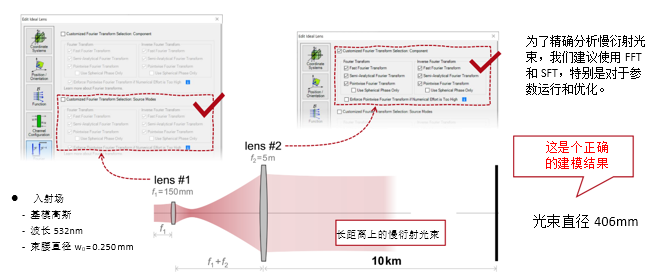 F�HU6o�910 P~{8L.w!>W D��FWO5Y�_ 2. 实例#2:忽略透镜间的衍射效应 �Wgh@X��B� 5\�z�<�xpJ
F�HU6o�910 P~{8L.w!>W D��FWO5Y�_ 2. 实例#2:忽略透镜间的衍射效应 �Wgh@X��B� 5\�z�<�xpJ 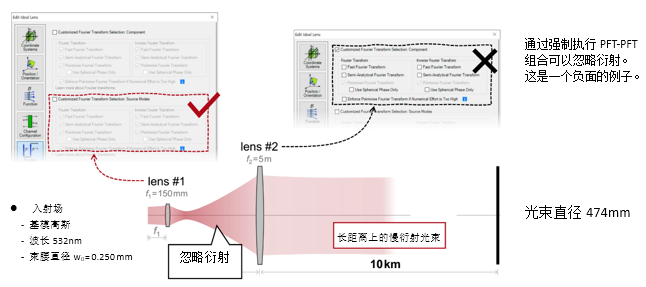 ^D+^~>f� G`n
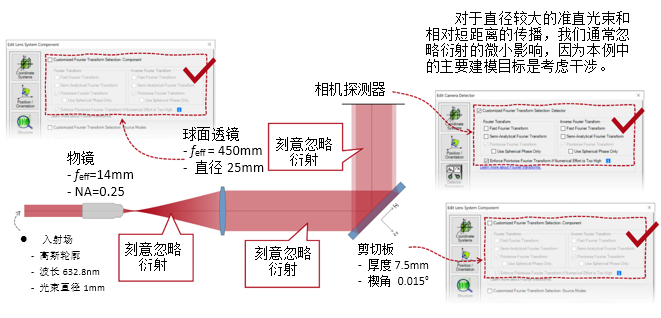
$A/9Q 实例#3:剪切干涉法的准直测试 -!_8>r;Q4� =3(Auchl$Y 1. 例#3:刻意忽略衍射 `K�5*Fj��x z�
���mip�
^D+^~>f� G`n
$A/9Q 实例#3:剪切干涉法的准直测试 -!_8>r;Q4� =3(Auchl$Y 1. 例#3:刻意忽略衍射 `K�5*Fj��x z�
���mip� 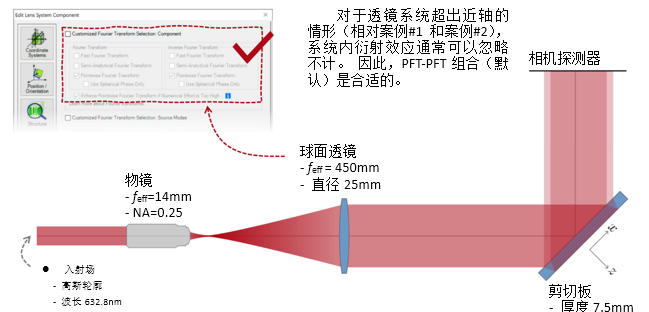 wjl�)yo�$z M\4�`�S�&� �cg3}33Z;6
wjl�)yo�$z M\4�`�S�&� �cg3}33Z;6
g=�4^u���*
 l~�;>Kj�Zg
l~�;>Kj�Zg 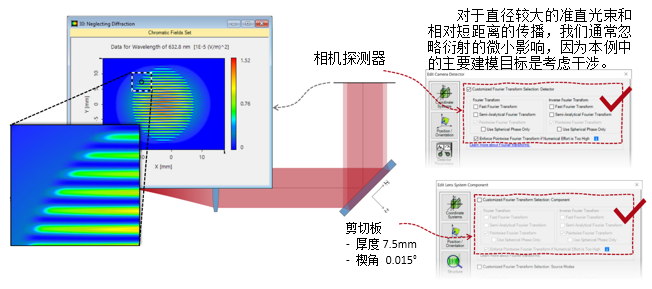 �
"&k(�lQ4 2. 实例#3:包含衍射 0)E�p�hsw� )�%F�w�f�b
�
"&k(�lQ4 2. 实例#3:包含衍射 0)E�p�hsw� )�%F�w�f�b 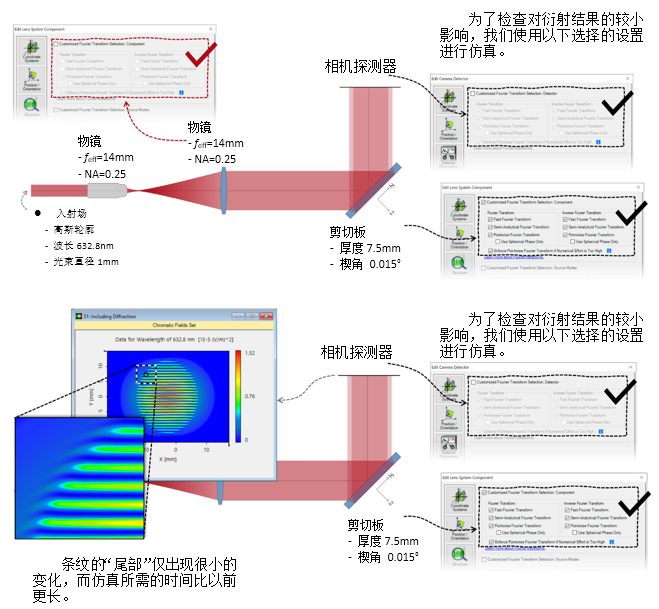 7�x�eq�s
q
7�x�eq�s
q