[技术]傅里叶变换设置——实例讨论 [复制链接]

VirtualLab Fusion包含了多种场求解器和函数。它们可以在空间(x)域或空间频率(k)域工作。为了将不同的求解器和函数简建立连接，实现复杂系统的建模，x域和k域之间的转换是至关重要的一步。 在本文中，我们将通过不同实例的讨论来示范如何对VirtualLab Fusion中有三种傅里叶变换算法进行设置。 YJlpP0;++  
<MlRy%3Z  
   "YUyM5X  
     /=zzym~<>  
2. 三种傅里叶变换 y~JCSzpU  
^&'&Y>  
\k{UqU+s  
 快速傅里叶变换(FFT) s:j"8ZH  
        - 对于不同数值计算，一种标准而高效的算法。 p=Nord  
 半解析傅里叶变换(SFT) S?W!bkfn  
        - 一种无需近似的高效重构。 H}OOkzwrA  
- 二次相的解析处理，类似chirp-z变换。 5V5E,2+ 0  

a$7}_kb  
 逐点傅里叶变换(PSF) vpy_piG|  
        - 受静态相位理论启发的一种近似方法，但采用纯粹的数学形式来表达。 HeagT(rN'  
- 对强波前相位是一种高效而精准的方法。 f#RI&I\  
Xj/U~  
         q][
{?  
JCu3,O!q  
   I<q=lK  
3. 每个元件的设置 x<'(b7{U0  
*TpzX y  
R6ynL([xh  
 傅立叶变换设置  q$$:<*Uy  
- 对于每个元件和探测器，都可以使用 “傅立叶变换”选项卡。 ~:Jw2 P2z
 
- VirtualLab Fusion自动选择所有激活的傅立叶变换选项；不选择未激活的选项。 a}Db9=  
- 傅立叶变换的组合影响自由空间中向前传播过程的建模。(这意味着不仅适用于元件前面的自由空间——它也适用于具有复杂通道配置的情况) }E5oa\1u  
sE4=2p`x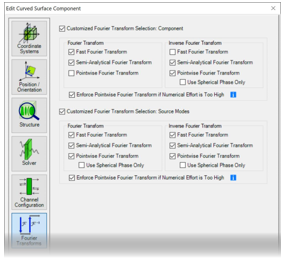  
gW
o`i  
   W|K"0ab  
4. 每个元件的设置 h 7
feZ_  
'/^bO#G:  
 傅里叶变换设置 j +j2_\  
o#KGEN
d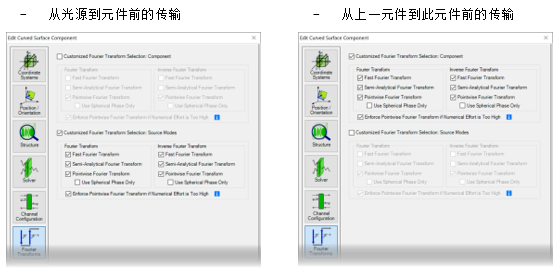  
       ?=:wIMV  
  qRg^Bp'VD#  
5. 默认的傅里叶变换设置 @(Mg>.P  
3"O)"/"Q.  
03ol!|X"9  
 光源模式和探测器的设置 VJ`c/EVIt  
- 对于光源模式和探测器，默认情况下将激活所有三个傅里叶变换选项。 ~c>*3*  
- 在特殊情况下，对于光源模式或探测器而言，衍射可能无关紧要。 我们将在下面的示例#1和示例#3中讨论这种情况。 o
T7
=  
H[ 6L!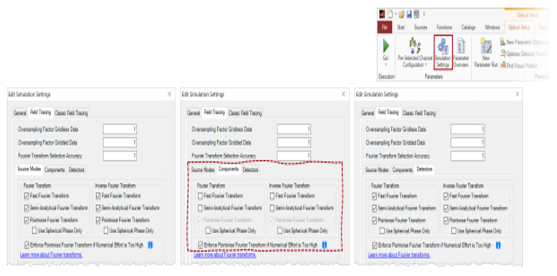  
olNgtSX  
  uqy b  
6. 特殊情况 ~Qzb<^9]  
     Y<U"}}  
vc.:du  
 多表面元件 tZS-e6*S  
- 对下列情况应当特别考虑 ;P9P2&c8c  
•透镜系统元件 )J?Nfi%  
•球面透镜元件 SF.4["$  
- 此类组件可以理解为 &Q>)3]|p  
•一组曲面元件，以及 X<\y%2B|l  
•之间有一些自由空间 C9-IJj  
- 傅立叶变换选项也会影响介于两者之间的自由空间传播。 E5d?toZ,8"  
S^,1N4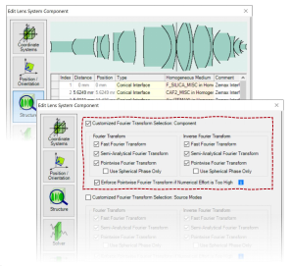  
R;9
H`L/>  
!`8WNY?K  
 在k域的元件 yoKl.U"&  
- 当元件的求解器/函数在k域中工作时，傅立叶逆变换选项不会产生任何影响 Byf5~OC  
- 这适用于以下情况 \\80c65-  
•平面表面元件 k}-@N;zq  
•分层介质元件 S/}6AX#F4  
•光栅元件 wYtL1D(  
•功能光栅元件 t:tT Zh  
t?NB#/#%x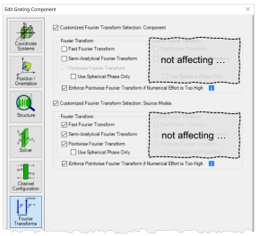  
(VYY-%N`  
  vkdU6CZO  
实例#1：低菲涅尔数系统中的针孔 R u^v!l`!7  
[AzQP!gi  
1. 实例#1：成像的光源模式 __p\`3(,'  
tETT\y|'  
14TA( v]T  
N zY}-:{  
[
h "*>J{  
2. 实例#1：系统内部包含的衍射效应 ViV"+b#gu  
PI>PEge!&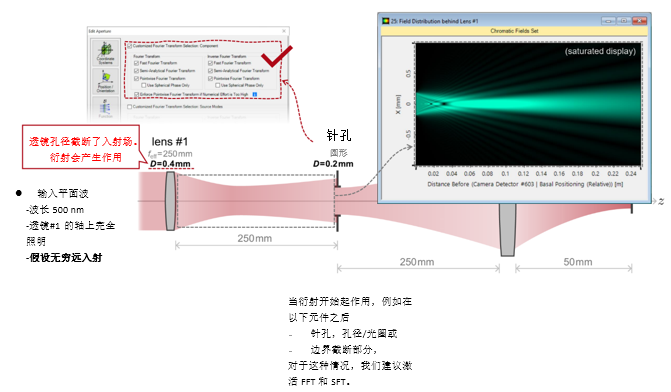  
+u%^YBr  
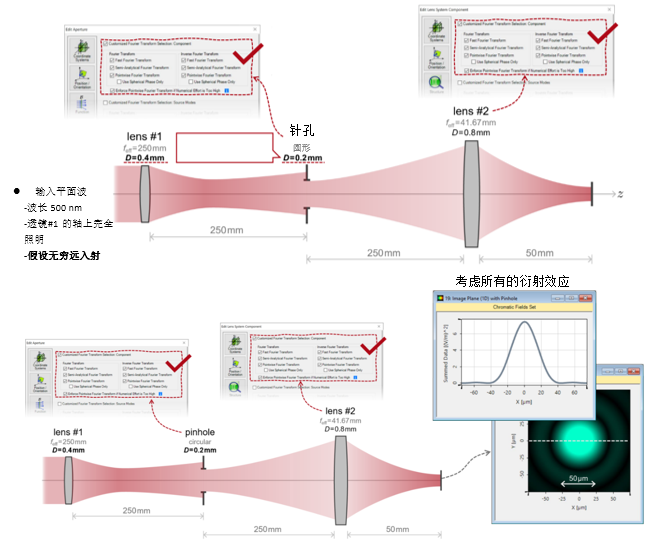i>!7/o  
     %Z@+K_X9x  
3. 实例#1：出瞳衍射法 e0O2>w  
Ekx3GM_]  
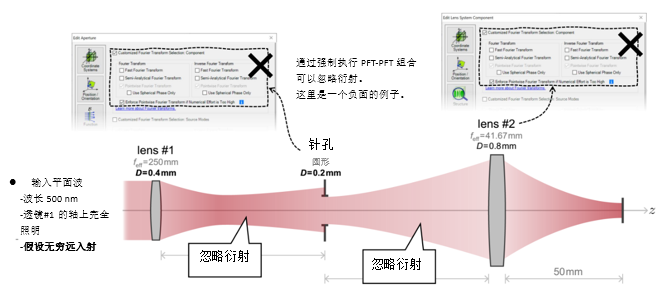pkjf5DWp  
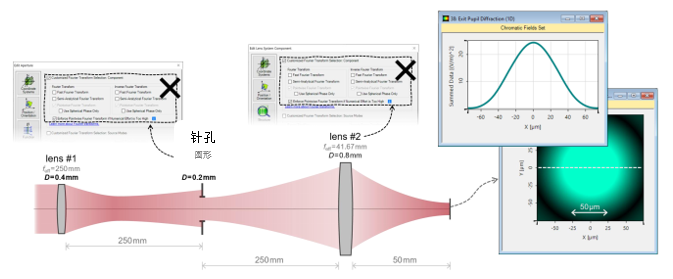YfBb=rN2s  
4. 实例#1：出瞳衍射与对比 (Dr g  
]>R|4K_  
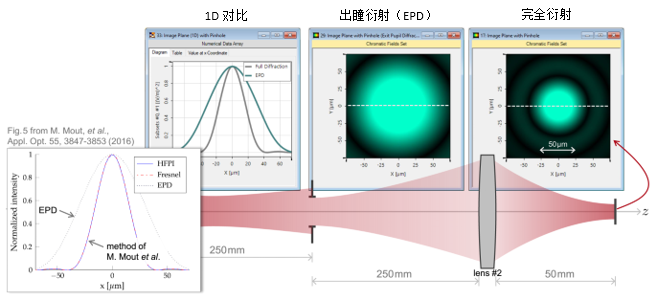6QsH?!bu  
  JcsJfTI  
实例#2：用于激光导星的无焦系统 Qq;` 9-&j  
W=T3spV  
1. 实例#2：包含所有可能的衍射 l6Hu(.Ls;j  
8$O=HE*  
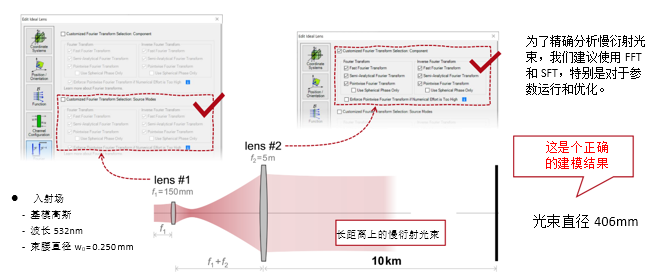H=E`4E#k  
yjZ]_.  
?bc-?<Xk  
2. 实例#2：忽略透镜间的衍射效应 Fw!wSzsk3  
$:M*$r^u  
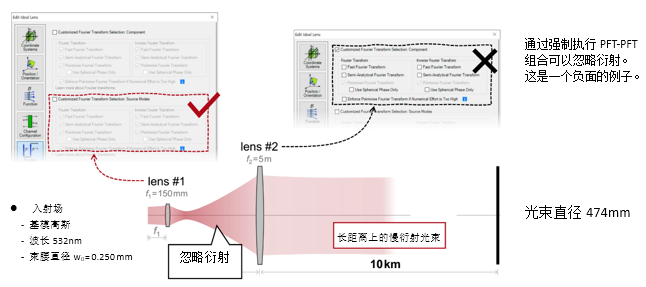 :[:5^R  
  ^|^ek  
实例#3：剪切干涉法的准直测试 t0_o.S  
t3ua5xw  
1. 例#3：刻意忽略衍射 fj X~"U  
c|<*w[%C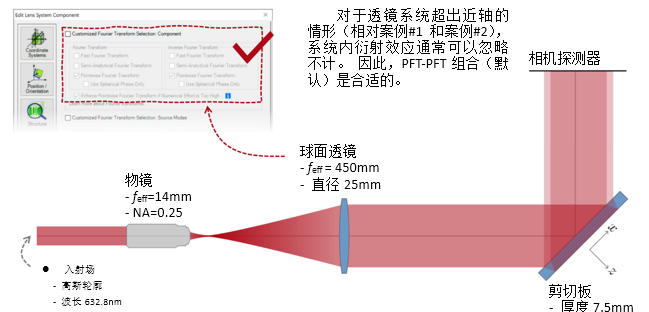  
(4_7ICFI  
-x~h.s,  
WPVur{?<  
V{17iRflf  
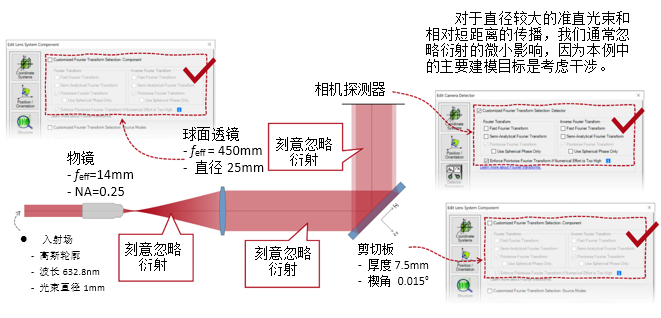
Wx#((T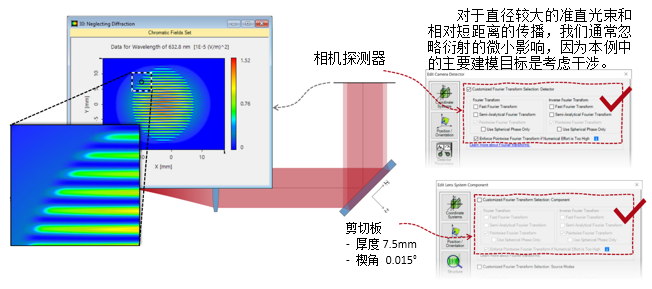  
!@mV$nTA  
2. 实例#3：包含衍射 T'9I&h%\  
)(~s-x^\z@  
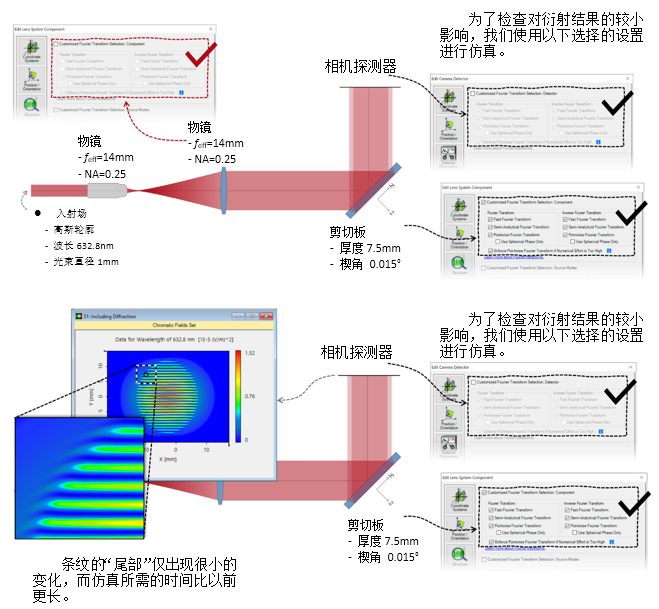1@Dp<Q