[技术]Savitzky-Golay滤波函数 [复制链接]

ZJoM?g~WFI  
W9&=xs6  
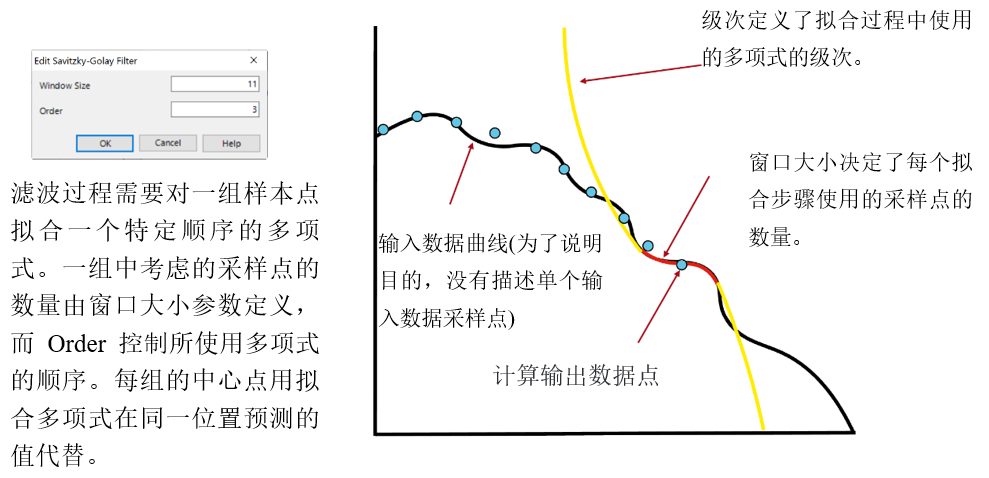
在测量信号或数据的情况下，很难(如果不是不可能的话)完全避免所有可能的噪声源，因为这些噪声源会干扰任何实验测量。但是，噪声的存在会干扰数据的重要特征(例如，测量光谱的半宽谱)。 Gv&V|7-f0  
        因此，有一些后期处理技巧可能会有所帮助。这里我们只讨论一个这样的工具:Savitzky-Golay滤波器，它通过对一组采样点执行回归算法来平滑局部噪声。在这个例子中，我们讨论了VirtualLab Fusion中这个特性的选项和效果，并以一个绿色LED灯在60 nm带宽下发射的光谱为例进行了测试。 ^iA9%zp  
%d@z39-;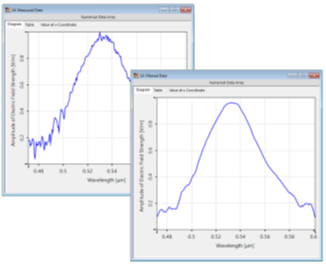  
h[ ZN+M  
?6!LL5a.  
2.如何进入Savitzky-Golay过滤器 e-;}3
66}  
`[A];]  
lE;!TQj:X  
        对于每个实值数据数组，都可以在下面找到Savitzky-Golay滤波器 ;uW FHc5@B  
        操作→ TeQV?ZQ#}  
杂项→ 9c],<;{'  
        Savitzky-Golay过滤器 Jm@oDME_E  
l (o~-i\M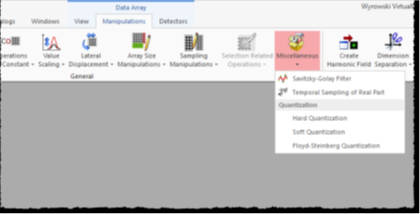  
U$g?!Yl0  
/v}`l  
3.可视化的过滤函数 z:O8Ls^\T  
4-w{BZuS  
!-bB559Nv  
*pd@.|^)m  
4.影响过滤器-窗口大小 ]:;&1h3'7  
xw%0>K[  
更大的窗口大小导致在拟合过程中考虑更多的采样点，因此曲线更平滑。 kAx4fE[c  
2oW"'43X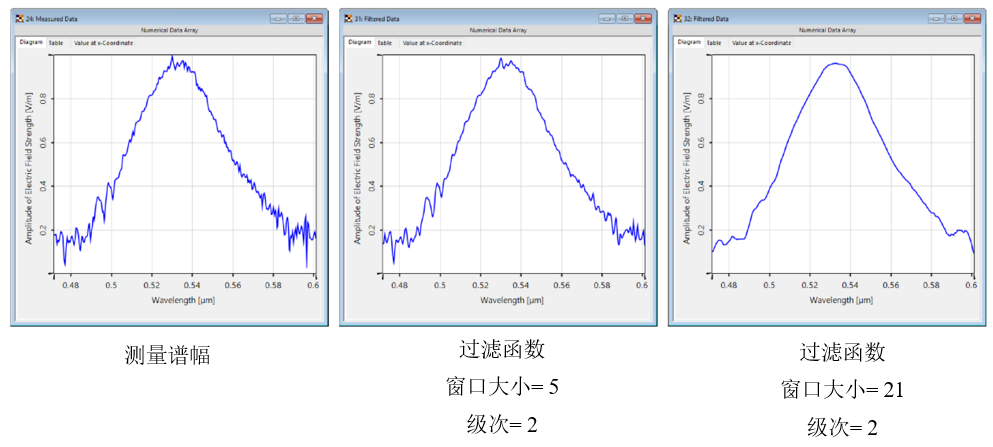  
Bvj0^fSm  
a*;b^Ze`v  
更高的阶数允许更详细的曲线，但反过来也可以保留局部噪声。 *j=% #  
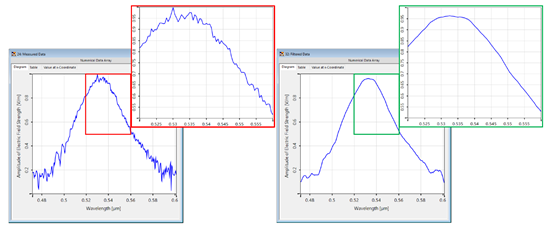
IV-{ve6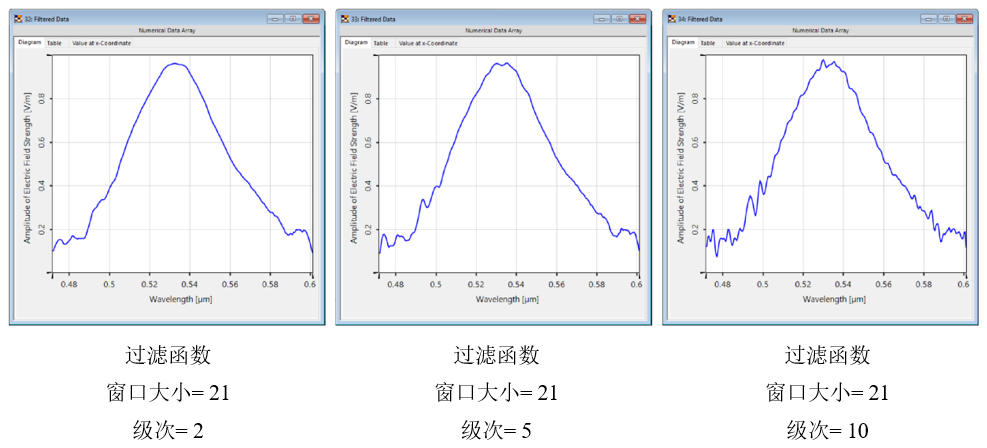  
|ZBw<f  
iLT}oKF2N;  
5.局部噪声过滤 p_ =z#  
Tw% 3p=  
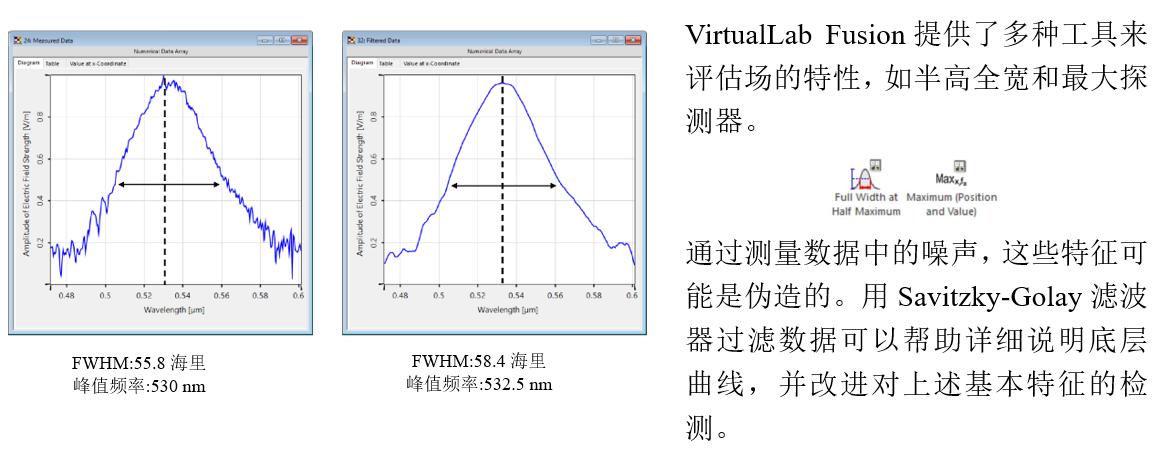
H]s.=.Ki  
i4Jc.8^9$  
6.FWHM 检测 ^.tg7%dJ  
mOSv9w#,  
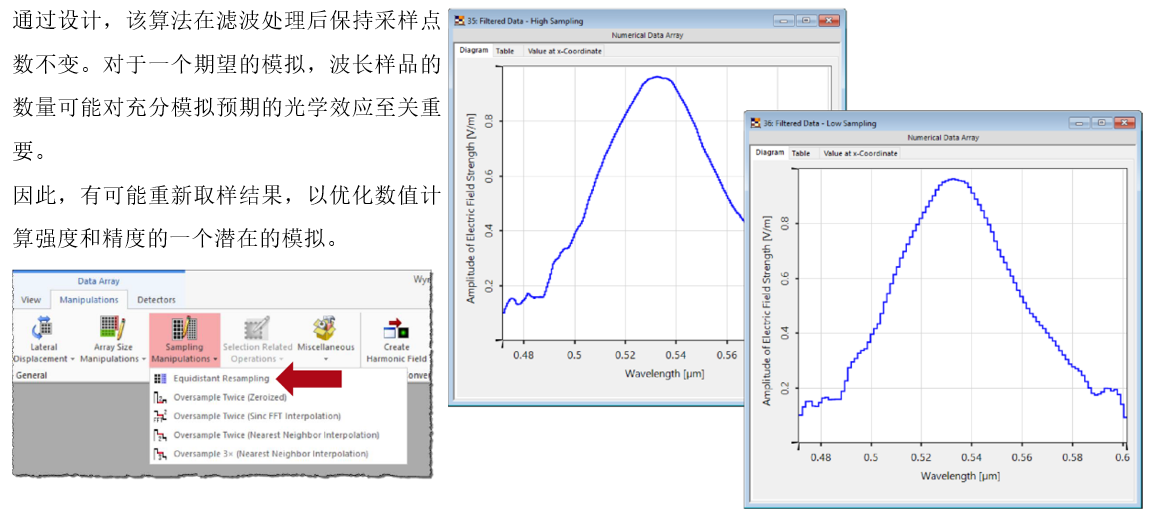
dx]>(e@(t{  
TC. ,V_  
7.等距的重采样 R]dg_Da  
ex|F|0k4}