切换到宽版
  • 广告投放
  • 稿件投递
  • 繁體中文
    • Zemax光学设计从入门到精通 Zemax光学设计从基础到实践 Zemax光学设计实践基础(陈家璧) ZEMAX光学系统设计实战
    讯技光电:VirtualLab Fusion独家供应商 微小光学与微透镜阵列 光学设计与光学元件 计算光学带来的成像革命
    发帖 回复
    返回列表
    • 173阅读
    • 0回复

    [技术]Savitzky-Golay滤波函数 [复制链接]

    		 上一主题 下一主题
    离线infotek
    科学家
     
    发帖
    5734
    光币
    22822
    光券
    0
    只看楼主 倒序阅读 楼主  发表于: 01-22
    1.摘要 g9gi7.'0  
    _FkIg>s  
    mb*|$ysPx  
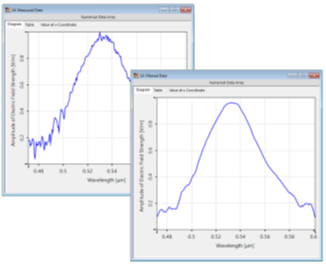
    在测量信号或数据的情况下，很难(如果不是不可能的话)完全避免所有可能的噪声源，因为这些噪声源会干扰任何实验测量。但是，噪声的存在会干扰数据的重要特征(例如，测量光谱的半宽谱)。 sPvjJr"s  
    因此，有一些后期处理技巧可能会有所帮助。这里我们只讨论一个这样的工具:Savitzky-Golay滤波器，它通过对一组采样点执行回归算法来平滑局部噪声。在这个例子中，我们讨论了VirtualLab Fusion中这个特性的选项和效果，并以一个绿色LED灯在60 nm带宽下发射的光谱为例进行了测试。 2*a5pFkb  
    }70A>JBw  
     Wv]ODEd  
    fPq)Lx1'  
    2.如何进入Savitzky-Golay过滤器 f7:}t+d  
    ##nC@h@  
    RKy!=#;17  
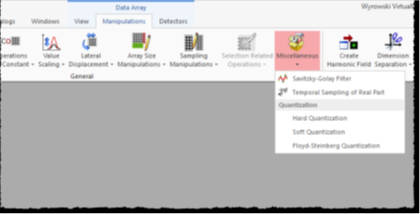
    对于每个实值数据数组，都可以在下面找到Savitzky-Golay滤波器 qm< mw"]  
    操作→ C/MQY:X4  
    杂项→ Xo3@-D_c!c  
    Savitzky-Golay过滤器 rDv`E^\  
    >DR$}{IV  
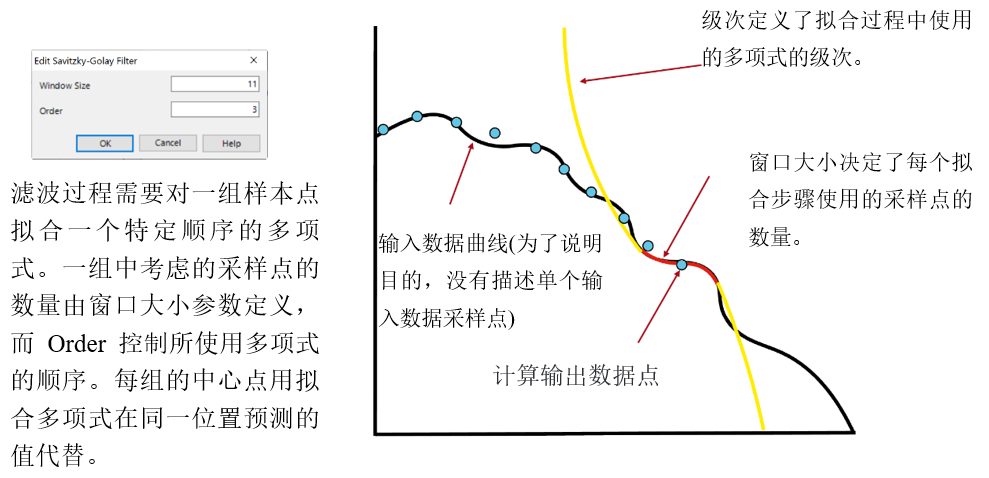
     1 Q*AQYVY  
    H7}f[4S%  
    3.可视化的过滤函数 vQy+^deW  
    e?+&2zMq  
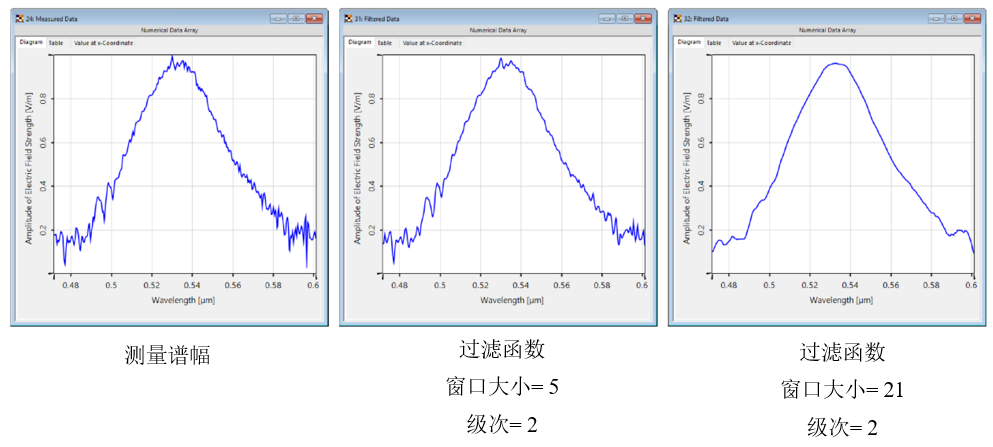
     {43 J'WsJ  
    p{AX"|QM"  
    4.影响过滤器-窗口大小 }J $\<ZT  
     ;cGY  
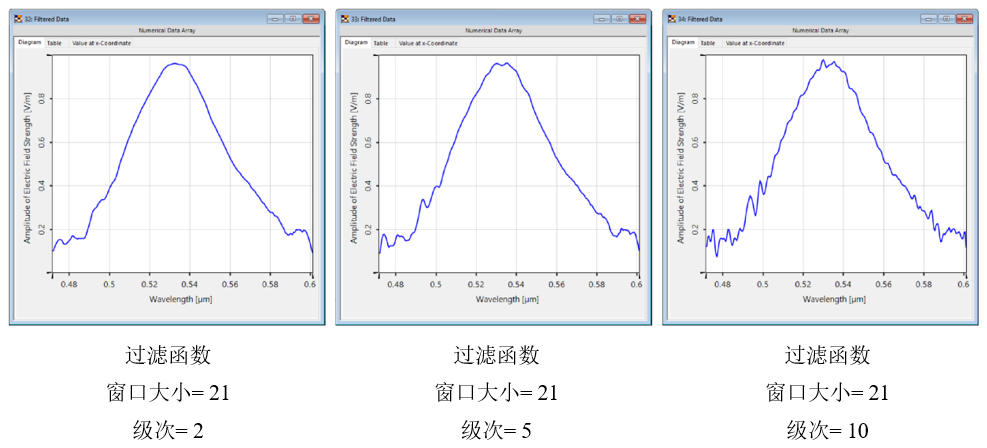
    更大的窗口大小导致在拟合过程中考虑更多的采样点，因此曲线更平滑。 U\-=|gQ'  
    h}Lrpr2r  
     w9675D+  
    DA>TT~L  
    更高的阶数允许更详细的曲线，但反过来也可以保留局部噪声。 f /t`B^}@  
    iw{^nSD  
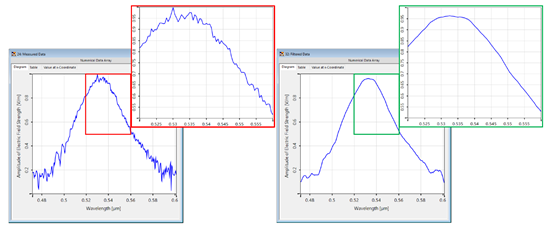
     ~>XqR/v  
    >Q:h0b_$U  
    5.局部噪声过滤 TT={>R[B  
    gv,1 CK  
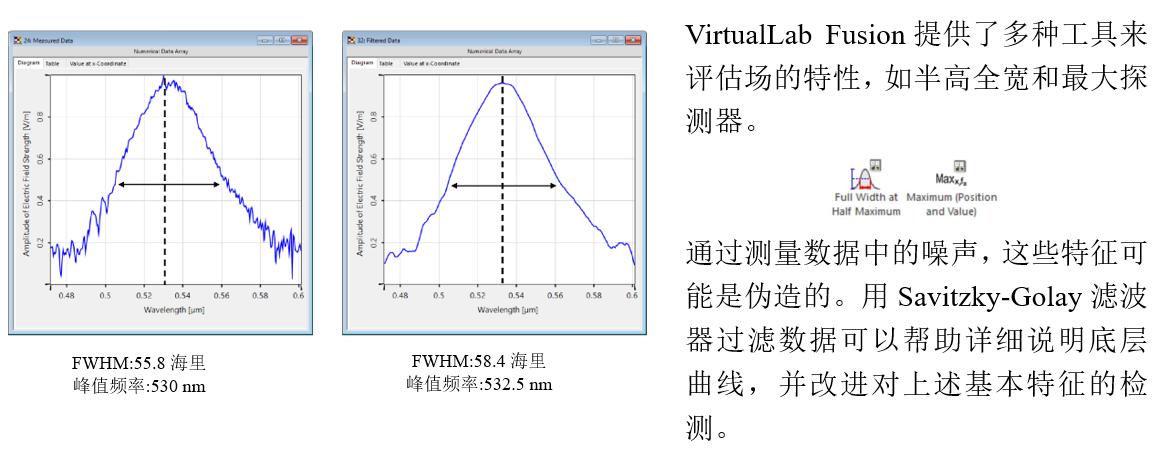
     [DvQk?,t  
    MqRJ:x  
    6.FWHM 检测 5]zH!>-F  
    KBa0  
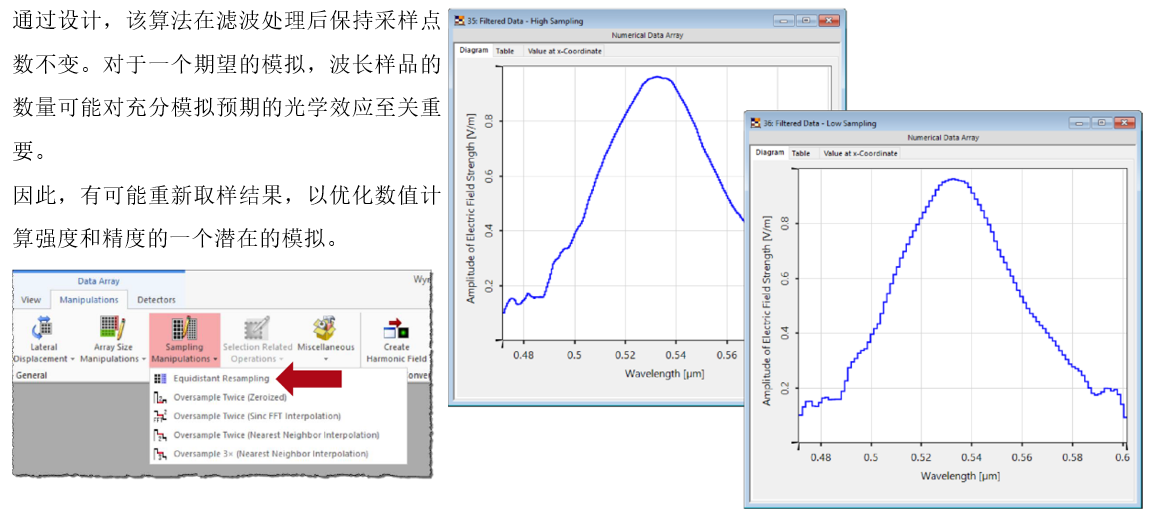
     N v6=[_D  
    Z29aRi  
    7.等距的重采样 Q9i[?=F:z  
    q4Mv2SPT  
     ij?Ww'p9>  
     
    回复
    举报
    分享到
    发帖 回复
    返回列表