-
UID:317649
-
- 注册时间2020-06-19
- 最后登录2026-03-04
- 在线时间1934小时
-
-
访问TA的空间加好友用道具

|
摘要 }xb?C""q^q
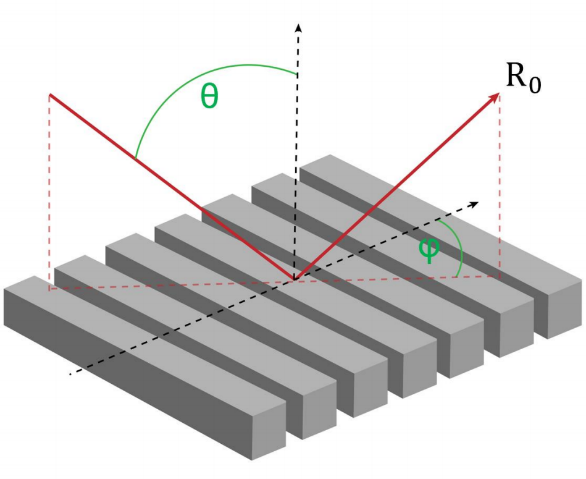
�Wi"3kps q 光栅结构广泛应用于各种光学应用场景,如光谱仪、近眼显示系统、脉冲整形等。快速物理光学软件VirtualLab Fusion通过使用傅里叶模态方法(FMM,也称为RCWA),为任意光栅结构的严格分析提供了通用和方便的工具。为此,复杂的一维或二维周期结构可以使用界面和调制介质进行配置,这允许任何类型的光栅形貌进行自由的配置。在此用例中,详细讨论了衍射级次的偏振态的研究。 d cG)�ql4d �1x3>XN]�a
 Bgf'Hm%��r PZYVLUw
` 任务说明 c�*D�Ba]u2 >ca w
��: Bgf'Hm%��r PZYVLUw
` 任务说明 c�*D�Ba]u2 >ca w
��:  @;b @O�
�_ �LKsK��!�X 简要介绍衍射效率与偏振理论 +zI�Nn�X� 某个衍射级次(𝑛)的效率表示有多少的辐射功率被衍射到这个特定的级次中。它是由复数值瑞利系数计算出来的,瑞利系数包含了每个衍射级次(矢量)电磁场的全部信息。瑞利系数本身是由FMM对光栅的特征值问题进行严格分析的结果。 �E�0�6)&tF 如果在TE/TM坐标系(CS)中给出瑞利系数,则可以计算衍射效率: �w^=�uq3X? @;b @O�
�_ �LKsK��!�X 简要介绍衍射效率与偏振理论 +zI�Nn�X� 某个衍射级次(𝑛)的效率表示有多少的辐射功率被衍射到这个特定的级次中。它是由复数值瑞利系数计算出来的,瑞利系数包含了每个衍射级次(矢量)电磁场的全部信息。瑞利系数本身是由FMM对光栅的特征值问题进行严格分析的结果。 �E�0�6)&tF 如果在TE/TM坐标系(CS)中给出瑞利系数,则可以计算衍射效率: �w^=�uq3X? 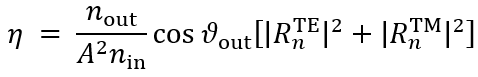 �8�}.V[,]6 其中,n_in/n_out为覆盖层和衬底层的折射率,ϑ_in/ϑ_out为所分析的阶次的入射角和衍射角。此外,𝐴表示辐射光的振幅。 G�W�C�U�9n 如果瑞利系数沿𝑥、𝑦和𝑧给出瑞利系数,则必须应用以下方程: >E\U$}�WCG �8�}.V[,]6 其中,n_in/n_out为覆盖层和衬底层的折射率,ϑ_in/ϑ_out为所分析的阶次的入射角和衍射角。此外,𝐴表示辐射光的振幅。 G�W�C�U�9n 如果瑞利系数沿𝑥、𝑦和𝑧给出瑞利系数,则必须应用以下方程: >E\U$}�WCG 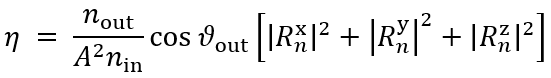 kV�Y��0
�E 因此,必须考虑所给出的瑞利系数的坐标系。默认情况下,光栅坐标系中为 kV�Y��0
�E 因此,必须考虑所给出的瑞利系数的坐标系。默认情况下,光栅坐标系中为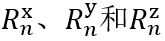 。 iu.$P-��s� $X� �]t}�= 。 iu.$P-��s� $X� �]t}�=
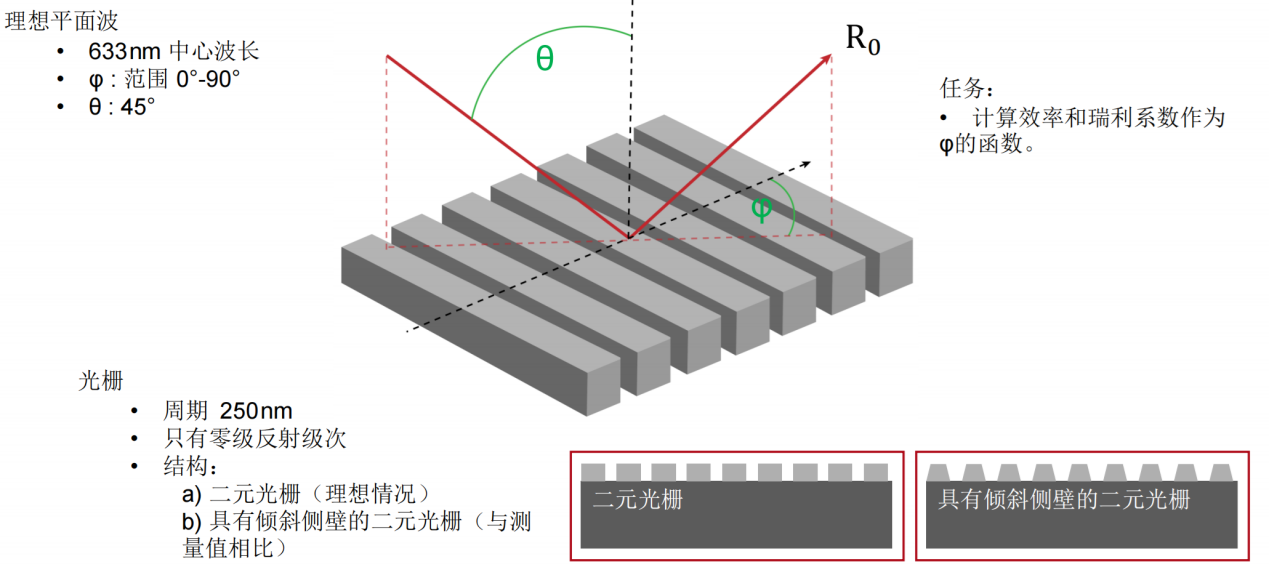
光栅结构参数 v��"8i2�+j 研究了一种矩形光栅结构。 D0*�+7��n3 为了简化设置,选择光栅配置,只允许零阶(R_0)反射传播。 rk7d7`��V 根据上述参数选择以下光栅参数: 3ahbv%y� 光栅周期:250 nm �.:9�XpKbt 填充因子:0.5 16|m�iK[@� 光栅高度:200 nm ��S �'��(K 材料n_1:熔融石英(来自目录) yP*oRV%�uX 材料n_2:二氧化钛(来自目录) kR]AW60�OE f|NWn�`#bY 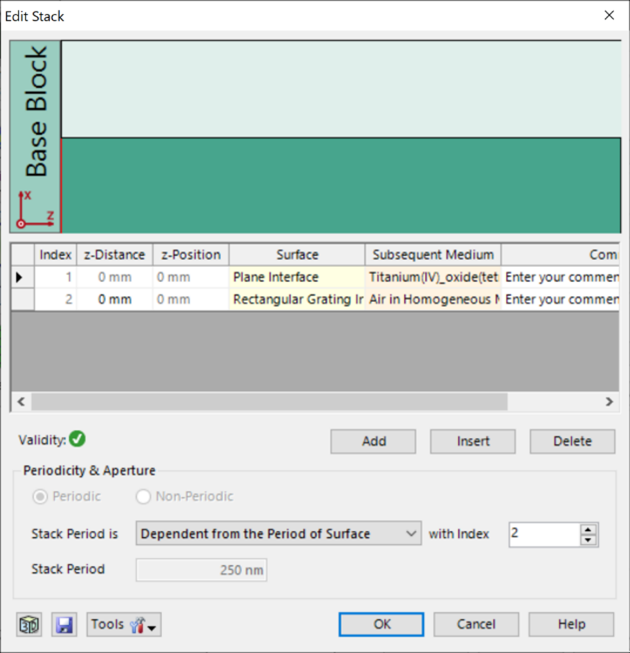 )�Pj4�_$uM Dwbt^{N��^ 偏振态分析 8\BYm|%�aa 现在,用TE偏振光照射光栅,并应用圆锥入射角(𝜑)变量。 7Rl/F1G o} 如前所述,瑞利系数的平方振幅将提供关于特定级次的偏振态的信息。 � BRF4��p: 为了接收瑞利系数作为检测器的结果,需要选择光栅级次分析器件中的单个级次输出,并选择所需的系数。 [+�(f��N�� T_�I� A�pC )�Pj4�_$uM Dwbt^{N��^ 偏振态分析 8\BYm|%�aa 现在,用TE偏振光照射光栅,并应用圆锥入射角(𝜑)变量。 7Rl/F1G o} 如前所述,瑞利系数的平方振幅将提供关于特定级次的偏振态的信息。 � BRF4��p: 为了接收瑞利系数作为检测器的结果,需要选择光栅级次分析器件中的单个级次输出,并选择所需的系数。 [+�(f��N�� T_�I� A�pC 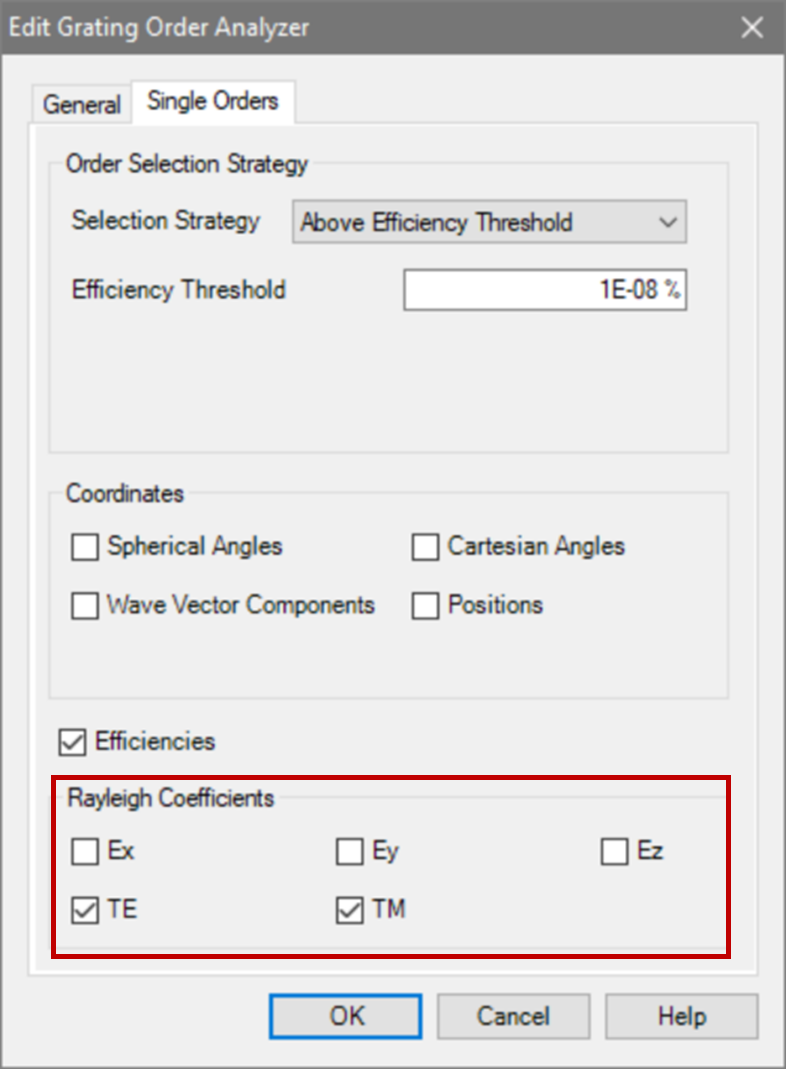 !�vGJ���7� ?O.��'_YS� 模拟光栅的偏振态 [�n�2)6B\/ !�vGJ���7� ?O.��'_YS� 模拟光栅的偏振态 [�n�2)6B\/
;9�)A+bD�]
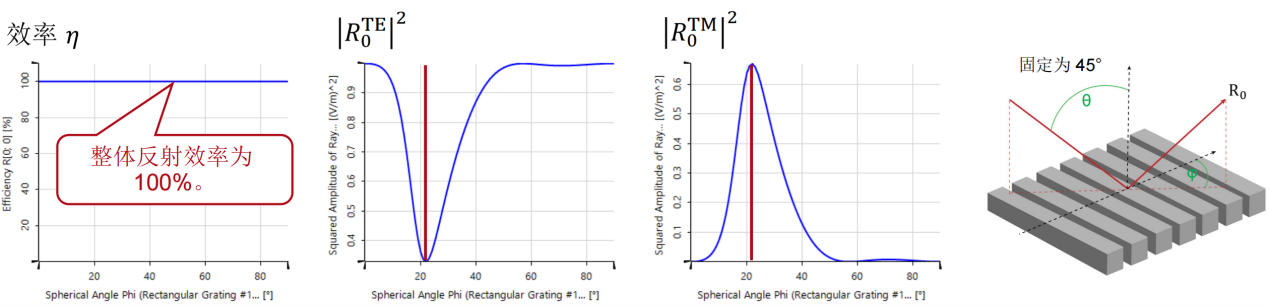 byN4��?3�F �����>7(�7 瑞利系数现在提供了偏振态的信息: (�y�v�)zg9 在圆锥入射角为0(𝜑=0)时, byN4��?3�F �����>7(�7 瑞利系数现在提供了偏振态的信息: (�y�v�)zg9 在圆锥入射角为0(𝜑=0)时,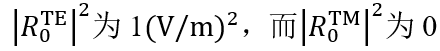 。这说明衍射光是完全偏振的。 ��
hpOK�9� 对于𝜑=22°, 。这说明衍射光是完全偏振的。 ��
hpOK�9� 对于𝜑=22°,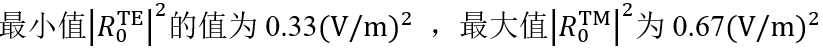 。此时,67%的光是TM偏振的。 t�x�F�c�V� 对于𝜑>50°,系数接近为常数,因此偏振态也是常数。 V1�
{'d[E* $LHF=��tYS Passilly等人更深入的光栅案例。 4cZlQ3OE�. Passilly等人的工作研究并优化了亚波长光栅下衍射光谱的偏振态,以获得不同状态之间的高度转换。 aSH �=|Jnc 因此,他们将模拟结果与制作样品的测量数据进行了比较。 �5�z@QA�Q� 。此时,67%的光是TM偏振的。 t�x�F�c�V� 对于𝜑>50°,系数接近为常数,因此偏振态也是常数。 V1�
{'d[E* $LHF=��tYS Passilly等人更深入的光栅案例。 4cZlQ3OE�. Passilly等人的工作研究并优化了亚波长光栅下衍射光谱的偏振态,以获得不同状态之间的高度转换。 aSH �=|Jnc 因此,他们将模拟结果与制作样品的测量数据进行了比较。 �5�z@QA�Q�
PD`�EtkUnv
 H�q0O!Z��v !I+F�8p �� 光栅结构参数 .s`7n
*xz� 在本文中,研究了两种不同的制备光栅结构。 0ra+�MQB�g 由于加工造成的光栅的理想二元形状的一些偏差是可以预料的,而且确实可以观察到:在基板和侧壁上存在不完全平行的欠刻蚀部分。 @jT=SF�f�� 由于缺少关于制作结构的细节,我们将其简化为VirtulLab Fusion中的模拟。 hO�..����j 但是如果有可用数据,就可以详细分析光栅的复杂形状。 JK^pb0�i�h H�q0O!Z��v !I+F�8p �� 光栅结构参数 .s`7n
*xz� 在本文中,研究了两种不同的制备光栅结构。 0ra+�MQB�g 由于加工造成的光栅的理想二元形状的一些偏差是可以预料的,而且确实可以观察到:在基板和侧壁上存在不完全平行的欠刻蚀部分。 @jT=SF�f�� 由于缺少关于制作结构的细节,我们将其简化为VirtulLab Fusion中的模拟。 hO�..����j 但是如果有可用数据,就可以详细分析光栅的复杂形状。 JK^pb0�i�h
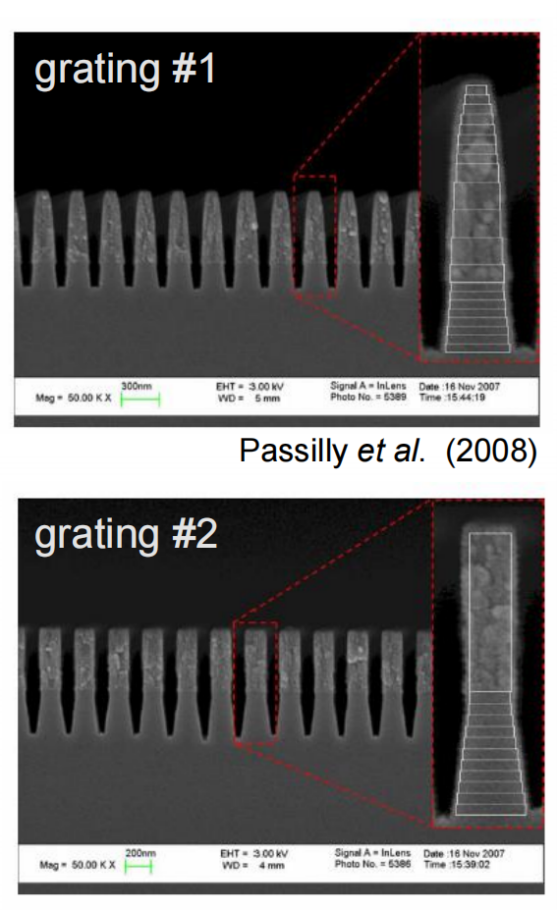 w�t�1Y&��D ��W��F`��� 光栅#1——参数
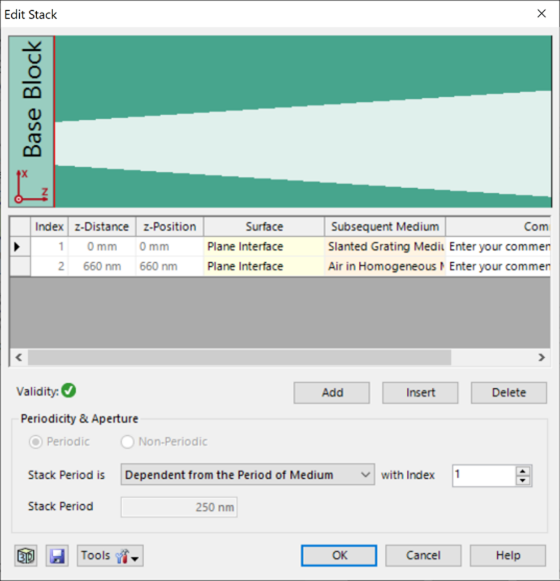
)�vy_m_f& 假设侧壁倾斜为线性。 W�f>=^ ~` 忽略了衬底中的欠刻蚀部分。 l;vA"�b=]� 为了实现光栅脊的梯形形状,采用了倾斜光栅介质。 f�@�H>by
N 光栅周期:250 nm U{����ZKxE 光栅高度:660 nm a~A"u�L�BR 填充因子:0.75(底部) ~NZ}@J{00_ 侧壁角度:±6° |6T"�T ��P n_1:1.46 >+F +"�NAN n_2:2.08 ��O�J,��Z w�t�1Y&��D ��W��F`��� 光栅#1——参数
)�vy_m_f& 假设侧壁倾斜为线性。 W�f>=^ ~` 忽略了衬底中的欠刻蚀部分。 l;vA"�b=]� 为了实现光栅脊的梯形形状,采用了倾斜光栅介质。 f�@�H>by
N 光栅周期:250 nm U{����ZKxE 光栅高度:660 nm a~A"u�L�BR 填充因子:0.75(底部) ~NZ}@J{00_ 侧壁角度:±6° |6T"�T ��P n_1:1.46 >+F +"�NAN n_2:2.08 ��O�J,��Z
&�O|q��x~(
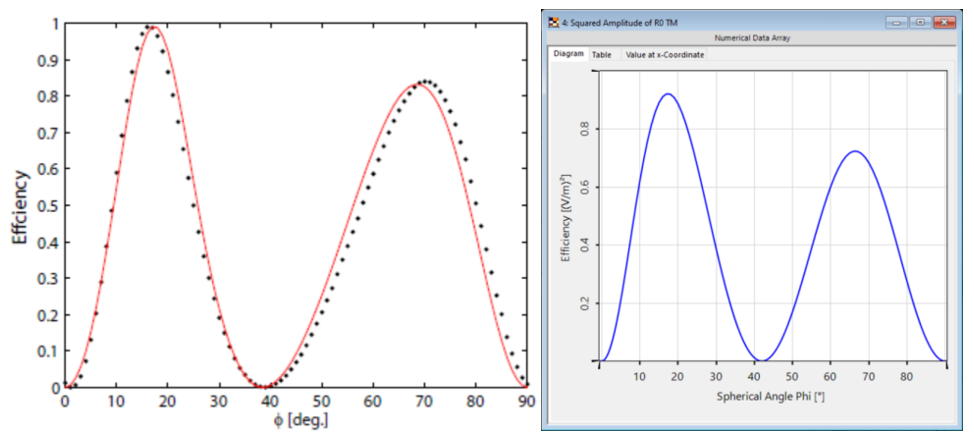
 O��i$$vjs2 #waK^B)�<a 光栅#1——结果 91:T�E8?Z� 这两幅图对比之下匹配度很高,特别是图表的趋势。 i?IV"*Ob1N 与参考文献相比,仿真中光栅结构进行了简化,存在一些小的偏差。由于缺乏关于实际的更详细的光栅结构的数据,这种简化是必要的。 G���[s/M\l �*#c^.4$�' O��i$$vjs2 #waK^B)�<a 光栅#1——结果 91:T�E8?Z� 这两幅图对比之下匹配度很高,特别是图表的趋势。 i?IV"*Ob1N 与参考文献相比,仿真中光栅结构进行了简化,存在一些小的偏差。由于缺乏关于实际的更详细的光栅结构的数据,这种简化是必要的。 G���[s/M\l �*#c^.4$�'
 ?Suv.!wfLl z]n&�,q,5g 光栅#2——参数 )mE67{YJh~ 假设光栅为矩形。 0s%]%2O��N 忽略了衬底中的欠刻蚀部分。 r)Fd�3)e � 矩形光栅足以表示这种光栅结构。 �G������ ; 光栅周期:250 nm ?jH�u�,��� 光栅高度:490 nm C0�-,�<X�� 填充因子:0.5 v\Ed�f;�(� n_1:1.46 Dt
�Ry%fA_ n_2:2.08 �EBx!q8zz TM0�DR'.� ?Suv.!wfLl z]n&�,q,5g 光栅#2——参数 )mE67{YJh~ 假设光栅为矩形。 0s%]%2O��N 忽略了衬底中的欠刻蚀部分。 r)Fd�3)e � 矩形光栅足以表示这种光栅结构。 �G������ ; 光栅周期:250 nm ?jH�u�,��� 光栅高度:490 nm C0�-,�<X�� 填充因子:0.5 v\Ed�f;�(� n_1:1.46 Dt
�Ry%fA_ n_2:2.08 �EBx!q8zz TM0�DR'.� 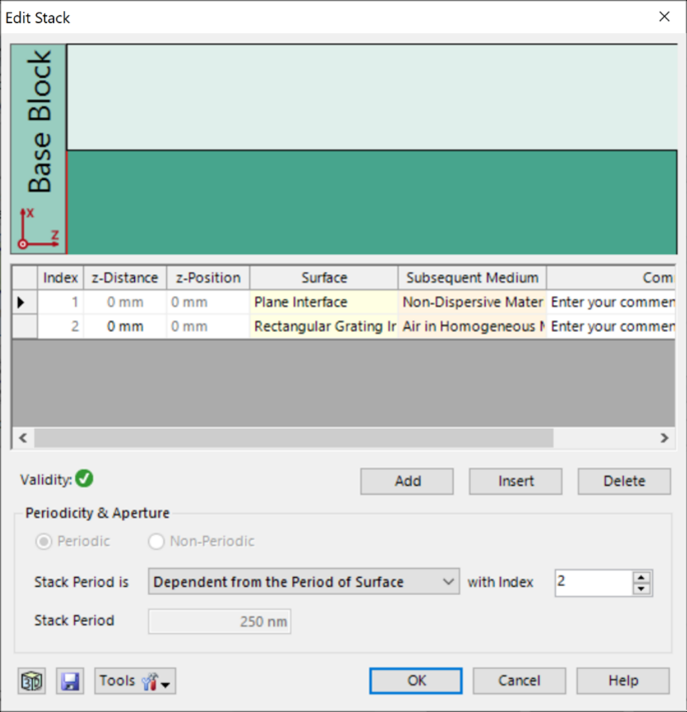 Rkh
^|�_<! p��^U#1c�� 光栅#2——结果 RxXiSc`�^z 这两幅图对比之下再次显示出非常好的匹配度,特别是图表的趋势。 Q)Z�bnR2Z8 与参考文献相比,仿真中光栅结构进行了简化,存在一些小的偏差。由于缺乏关于实际的更详细的光栅结构的数据,这种简化是必要的。 �{z*`*
O@ % QI6`@Y"� Rkh
^|�_<! p��^U#1c�� 光栅#2——结果 RxXiSc`�^z 这两幅图对比之下再次显示出非常好的匹配度,特别是图表的趋势。 Q)Z�bnR2Z8 与参考文献相比,仿真中光栅结构进行了简化,存在一些小的偏差。由于缺乏关于实际的更详细的光栅结构的数据,这种简化是必要的。 �{z*`*
O@ % QI6`@Y"� 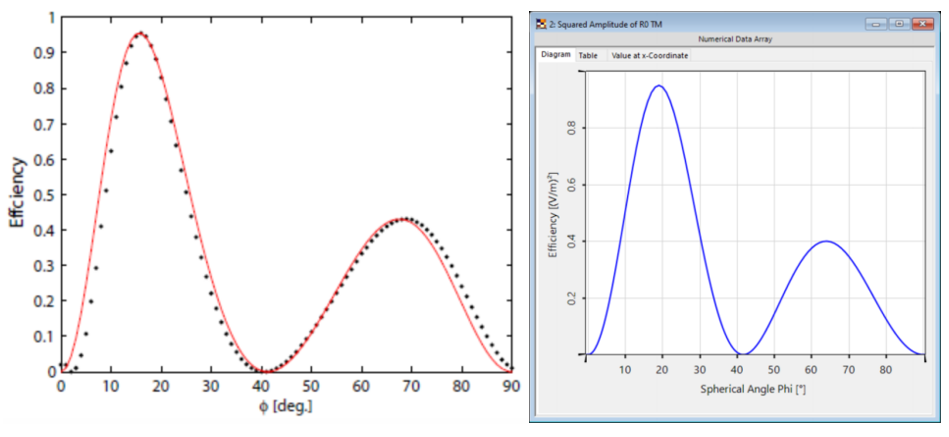 �"Tc[1{�eI �"Tc[1{�eI
|