简介 �/kB|�1gFj �;�L~p�|sF 激光系统常使用一个称为空间滤波器的小孔。通过去除
光束中的高阶模和噪声,空间滤波器是一种用于提高激光质量的技术。为了在FRED中准确
模拟激光通过一个空间滤波器,光在通过滤波器之后光场的重新合成是非常重要的。这样做将会精确的模拟在孔径上的裁剪。在本篇文章中,将会阐述Gabor分解的光合成技术。
w2{g�,�A�| r<c #nD�~K 相干光的高斯子束模型
R_1�q�n�� �YLOwQj�'� 通过使用一个称为高斯光束分解(GBD)的技术,可以在FRED中实现相干光的模拟。光场被分成独立的高斯子束,相互之间是相干传播的。每个子束由一组
光线表示(图1),主光线沿着子束的轴。八个二级光线包括:代表光束腰的四个正交二级束腰光线,和代表光束发散度的四个正交二级发散光线。在光线追迹的过程中,主光线决定了所有二级光线的命运:如果主光线通过了一个孔径,假设,则所有的二级光线必须通过该孔径。这项使用光线来表示高斯子束的技术被称为复合光线追迹。
{~N3D4n^� 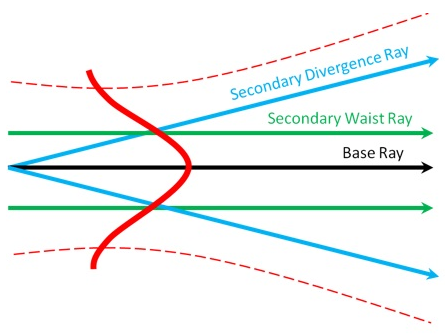
图1 高斯子束的复合光线表示
�@T�zvT3\q :"QfF@�Z�{ 如果激光在一个空间滤波器处聚焦,则在相干光线追迹中的大多数主光线将会通过孔径。这忽略了剪裁的影响。为了正确的模拟剪裁,在空间滤波平面的光场应该在孔径内重新采样,产生一组新的光线,用于通过系统的进一步传播。
�lpy:3`ti 19Ww3P�vQ; 14μm空间滤波器内的Gabor分解 i��%��;"[M �K]/��Od�� 在FRED中模拟的一个空间滤波系统如图2所示。创建了相干准直的He-Ne激光束。
光源由直径为6mm的椭圆孔径内的21*21条光线组成。光线通过
焦距为52mm的平凸
透镜。空间滤波器放置在焦点上。空间滤波器的直径是基于透镜焦距和光束直径计算而得。
�+j{Y�,t{4 0(y���:�$� 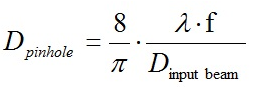 +-BwQ{92[: R,t�$"b�Od
+-BwQ{92[: R,t�$"b�Od 通过添加FRED自定义元件(Custom Element)可以创建空间滤波器小孔,它由半径为0.007mm的圆弧曲线描述。在空间滤波器位置处创建了一个1*1的吸收平面。在该平面上指定了一个分析面(64*64μm宽,257*257像素)来收集光场。绘制光场之后,用户需要右键点击并选择相干场操作/应用剪裁到场(Coherent Field Operations / Apply Clipping to Field),选择已经创建好的剪裁曲线。光场现在已经得到了正确的剪裁(图3)。
mnjs�(x<�m 图2 He-Ne激光束的空间滤波器
�83 I-�X95 图3 用空间滤波孔径剪裁光场的结果
Pc�C/_+2�� ��Vr=OYI'A 最后,剪裁区域内将会产生一组新的复合光线。使用Gabor分解可以实现它。在剪裁光场的图中,用户需要右键点击并选择相干场操作/合成场(Coherent Field Operations / Synthesize Field.)。相干场合成
参数如图4所示。
�'\"G{jU@� gC�uAF$o�� 最后一步是选择“追迹现有的(Trace Existing)”来模拟通过空间滤波器的光线传播。图5显示了通过具备光场合成的准直透镜后的辐照度分布,与忽略了空间滤波器剪裁的分布作比较。显然,光场合成精确的模拟了减小的光束直径和预期的衍射特性。
"(`2eX�R�n 图4 相干场的合成参数。Gabor分解是一种定向合成,它要求最大的子束半孔径。最大的光线位移设置为1以保证光束重叠。最大光线角由下一个元件的直径决定。在这个例子中,准直透镜最大角至少要达到8°。
�B�z /�@c) 图5 经过准直透镜的辐照度分布。左:光场已经使用空间滤波器正确的重新合成。右:没有光场合成,所有复合光线畅通无阻地通过空间滤波器,同时忽略了剪裁。
Gb��2�L }� <T�+!V-Pj* FRED具有使用高斯子束模拟相干光传输的能力。该方法适用于光线在自由空间传播,剪裁光束的
光学元件应该小心处理。正如空间滤波器,非常小的孔径需要光场的重新合成以精确的模拟光束的剪裁。使用一个简单的例子,Gabor分解已经证实可以准确的模拟激光系统中空间滤波器的影响。Gabor分解的其他应用包括:具备混合模式的空间滤波器的使用、单色仪缝隙孔径和杨氏缝隙/小孔干涉仪。
oC*=JJ�e, h2���~4G)J 参考文献 Y$�<D9f�s3 yNCEz��/4� [1] Herloski, R. et al “Gaussian Beam Ray-Equivalent Modeling and Optical Design”, Applied Optics, Vol. 22, No. 8, p. 1168-1174, April 1983 (Erratum, Applied Optics, Vol 22, No. 20, p 3151).
��|3shc,�7 [2] P. D. Einzinger, S. Raz and M. Shapiro, “Gabor Representation and Aperture Theory”, J. Opt. Soc. Am. A, 3 (4) (April 1986).