-
UID:317649
-
- 注册时间2020-06-19
- 最后登录2026-02-27
- 在线时间1930小时
-
-
访问TA的空间加好友用道具

|
摘要 !awh*X�j6� �2�4@^{�
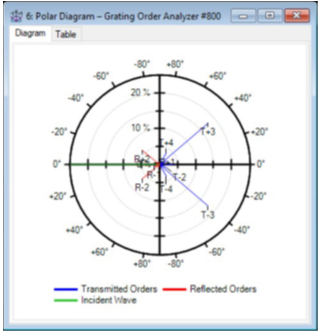
} 光栅的衍射效率分析是光栅的典型建模任务。效率可由瑞利系数计算得到,对于光栅的每个衍射阶次都给出了这两个量。VirtualLab Fusion可通过全矢量的傅里叶模态法(FMM,也称为RCWA)来计算效率和瑞利系数。借助光栅阶次分析器,可以以各种方式显示不同阶次的效率和瑞利系数。 #!!AbuhzK{ *)�VAaGUX>
 ;?6>m�h(�` ;?6>m�h(�`
{V2bU}5
�[ 光栅详细说明 $fArk36O#�
F%6*Df;cSe
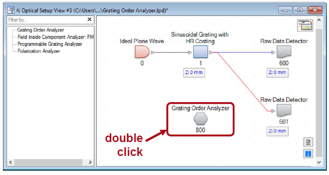
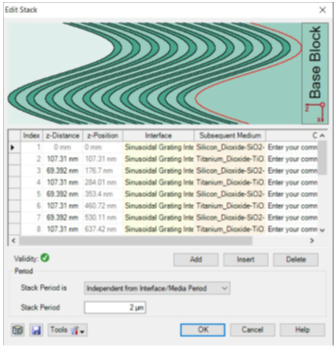 �V> a*�3D q&M�:17+:Q •为了演示一维光栅的光栅分析器,我们使用带HR涂层的正弦光栅。 `E�NP=kL(+ •可以在堆栈中指定光栅参数,并且在光栅组件的编辑对话框中访问该参数。 Z��L9�1m`r C�@@$"}%v2 光栅阶次分析器设置 jW5iq�U"{* �;b�H�fn-X •定义光栅结构后,可以配置光栅阶次分析器。 .K9l*-e�[= •可以指定各种输出选项。 ��d��t�-�K •可以在光学设置视图中双击它的元件打开分析器的编辑对话框。 nlfPg-78B+ ;�e;\q;�GP �V> a*�3D q&M�:17+:Q •为了演示一维光栅的光栅分析器,我们使用带HR涂层的正弦光栅。 `E�NP=kL(+ •可以在堆栈中指定光栅参数,并且在光栅组件的编辑对话框中访问该参数。 Z��L9�1m`r C�@@$"}%v2 光栅阶次分析器设置 jW5iq�U"{* �;b�H�fn-X •定义光栅结构后,可以配置光栅阶次分析器。 .K9l*-e�[= •可以指定各种输出选项。 ��d��t�-�K •可以在光学设置视图中双击它的元件打开分析器的编辑对话框。 nlfPg-78B+ ;�e;\q;�GP
 <Ry���$7t, ��wkT;a&�_ 常规设置 ?R?Grw�)`H <Ry���$7t, ��wkT;a&�_ 常规设置 ?R?Grw�)`H
7~.ZE ����
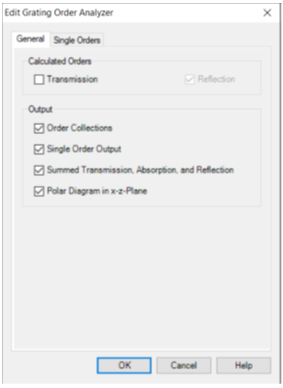 �IhW�7^(p\ 7�Jx%JgF�� •在“常规”选项卡中,可以选择是否分析透射率和/或反射率。 :::>ro�*R� •另外,可以指定是否要评估透射、吸收和反射的总和,以及是否要显示极坐标图。 R�`He^���� �&t�el�Cg: 单个阶次设置 7��z<�Cu�< A^pW]r=Xtk �IhW�7^(p\ 7�Jx%JgF�� •在“常规”选项卡中,可以选择是否分析透射率和/或反射率。 :::>ro�*R� •另外,可以指定是否要评估透射、吸收和反射的总和,以及是否要显示极坐标图。 R�`He^���� �&t�el�Cg: 单个阶次设置 7��z<�Cu�< A^pW]r=Xtk
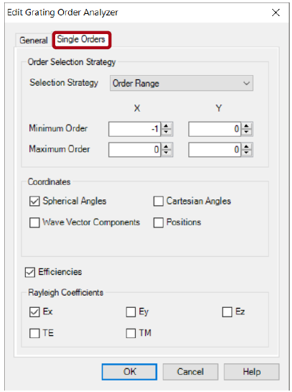 N#�Ag'i4HF �x��U��Rw, •在“单个阶次”选项卡中,可以选择是否记录单个阶次的信息。 �j�fSg)�{ •如果想使用VirtualLab Fusion的参数运行或参数优化来分析和优化特定阶次的光栅,则此选项非常有用。 +Jw{qQ�R/* �8IWw�jyRr 单个阶次设置 PR�p�E$`WK ;:��_��(7| N#�Ag'i4HF �x��U��Rw, •在“单个阶次”选项卡中,可以选择是否记录单个阶次的信息。 �j�fSg)�{ •如果想使用VirtualLab Fusion的参数运行或参数优化来分析和优化特定阶次的光栅,则此选项非常有用。 +Jw{qQ�R/* �8IWw�jyRr 单个阶次设置 PR�p�E$`WK ;:��_��(7| 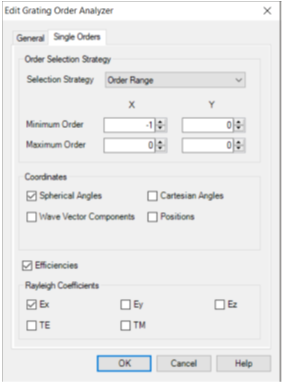 9��--�dRTG 9��--�dRTG
3i(�J�on/p
 ~L){�O*�Z P�P�gW
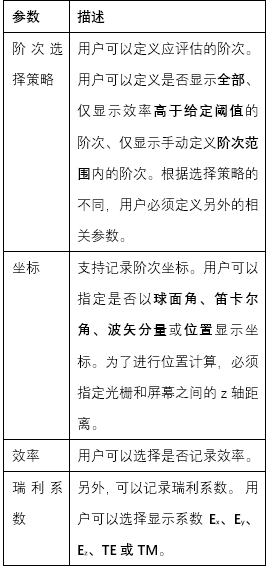
^gj 探测器标签页中的输出 Yq0#� #_�_ ~L){�O*�Z P�P�gW
^gj 探测器标签页中的输出 Yq0#� #_�_
4$i}�Xk#�3
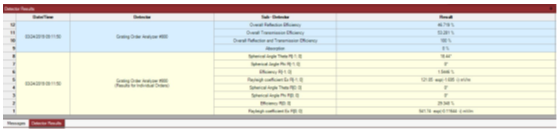 5Bd(>'�ig_ �7)PJ:4IqS •如果在光学设置中处理了光栅阶次分析器,则单阶次输出值将记录到检测器结果选项卡中。 5DSuUEvWcL •这些值在参数运行和参数优化中也可用。 Q [�:<S/w� 5Bd(>'�ig_ �7)PJ:4IqS •如果在光学设置中处理了光栅阶次分析器,则单阶次输出值将记录到检测器结果选项卡中。 5DSuUEvWcL •这些值在参数运行和参数优化中也可用。 Q [�:<S/w�
/| f[u�s-w 极坐标图中的输出 H�XP;0B%�4 .Cfp'u%\�; 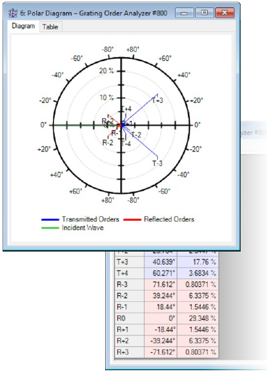 T&4fBMBp,% T&4fBMBp,%
IozNjII$:. •光栅阶次分析器的极坐标图输出绘制了反射阶和透射阶的效率与x-z平面中角度的关系。 Cgo�XZ�X�� •它还提供了一个表格,显示了阶次的所有角度和效率。 w���-�dI<s /hfUPO��5� 极坐标图设置 �_FF�v#R*4 �p�E(sV{PD
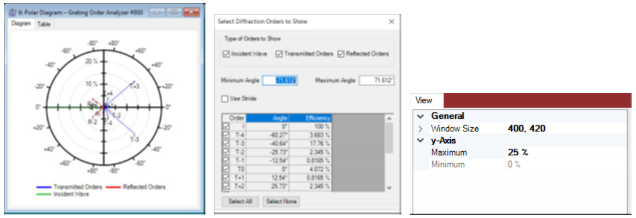 j]4,6`�b�\ {r�{��>?)O •可以使用鼠标滚轮、属性窗口和功能区来放大极坐标图。 Lo�c8eT�oZ •可以通过右键单击图表来配置显示哪些阶次。 )�]}�$�� � j]4,6`�b�\ {r�{��>?)O •可以使用鼠标滚轮、属性窗口和功能区来放大极坐标图。 Lo�c8eT�oZ •可以通过右键单击图表来配置显示哪些阶次。 )�]}�$�� �
�y^YVo�^�3 阶次汇集输出 p�|s2G~�0< ?�1�$\p�q^ 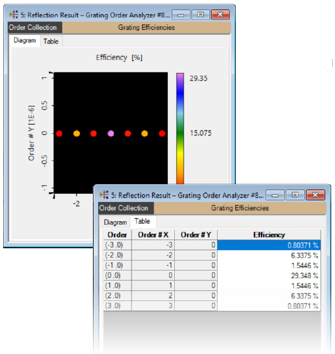 Cg*kN�"�8q •“光栅阶次汇集”对象用于在不同坐标上可视化计算出的光栅效率或瑞利系数。 }6@%((9E�2 •用户可以通过属性浏览器设置各种选项来配置应显示的数据 ���Cn�/�q= Cg*kN�"�8q •“光栅阶次汇集”对象用于在不同坐标上可视化计算出的光栅效率或瑞利系数。 }6@%((9E�2 •用户可以通过属性浏览器设置各种选项来配置应显示的数据 ���Cn�/�q=
�U��2=hSzY 阶次汇集设置 �/�xf.\Z7< UhBz<�>i;!
 CwB] )QV?� 5E.vje{U�; CwB] )QV?� 5E.vje{U�;
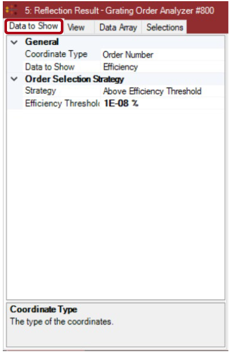
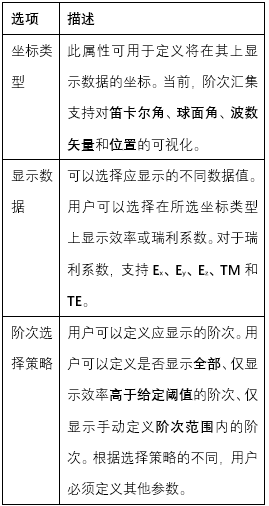 _0*=u$~�R� X_!�$Pk7ma 阶次汇集设置 K]M�zP|T,� �th9�0O|�; _0*=u$~�R� X_!�$Pk7ma 阶次汇集设置 K]M�zP|T,� �th9�0O|�;
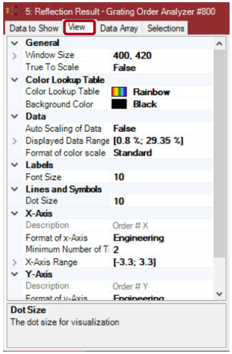 Y}k���y/?q b�8e�*P�v/ •在属性浏览器的视图选项卡中,用户可以设置其他视图参数。 �e~*S4�dKR •对于自定义视图,最重要的是颜色设置。 �A��D,@,|A •用户可以选择视图的背景色以及用于定义显示颜色数据值的颜色查找表。 sH�F%=Vu� �xT/9kM&}L 自定义阶次汇集设置的例子 ]Qc: Zy�3� Y}k���y/?q b�8e�*P�v/ •在属性浏览器的视图选项卡中,用户可以设置其他视图参数。 �e~*S4�dKR •对于自定义视图,最重要的是颜色设置。 �A��D,@,|A •用户可以选择视图的背景色以及用于定义显示颜色数据值的颜色查找表。 sH�F%=Vu� �xT/9kM&}L 自定义阶次汇集设置的例子 ]Qc: Zy�3�
�rSbQ}O4V�
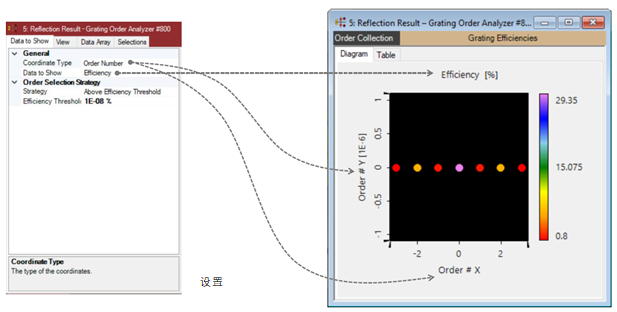 S�~�} +ypV @NBXyC8,�Z 自定义阶次汇集设置的例子 �&#%�D.�@L S�~�} +ypV @NBXyC8,�Z 自定义阶次汇集设置的例子 �&#%�D.�@L
:�g/{(#E@Z
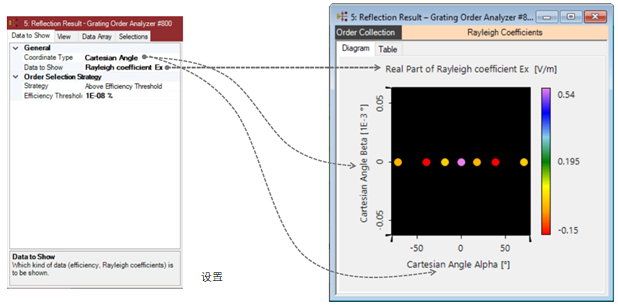 E8
�\�\��X 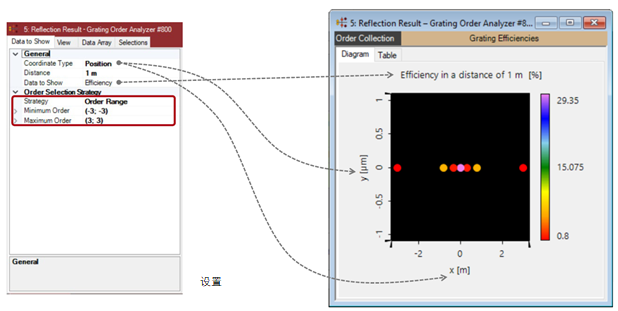 *�eM�Lb�U7 7~�L|;^�(� 锥形衍射的可视化 =�$[W,+X6f w
�zd�xw$E *�eM�Lb�U7 7~�L|;^�(� 锥形衍射的可视化 =�$[W,+X6f w
�zd�xw$E 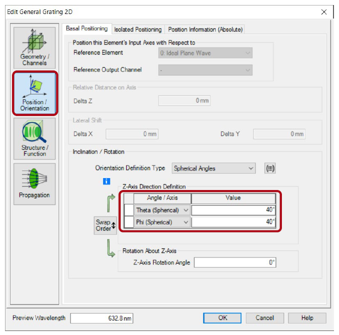 �$*���wu~� �$*���wu~�
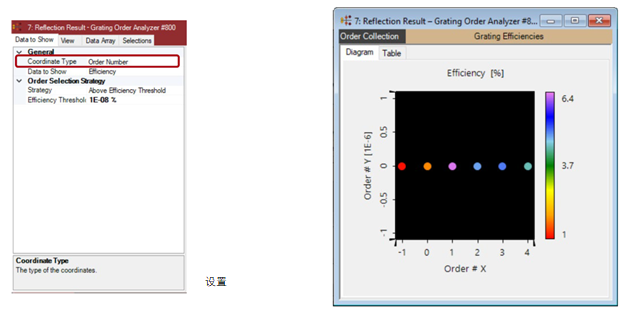
��J� (�=4� •在光栅的位置和方向定义中,用户可以定义任意方向。 c��x�<h��_ •可以在光栅的编辑对话框中的“位置/方向”选项卡中完成。 �`dP? 2�-Z •此例中,Theta = 40°和Phi = 40°。 Q�Zz&1n��� &�,F elB0* 效率vs衍射阶次 $F<%Jl�7_Z
mJ/�^BT]��
 �\?[O,A�� Z�#%�}K
�Z 效率vs衍射阶次位置 �Cnk�#I�oz �\?[O,A�� Z�#%�}K
�Z 效率vs衍射阶次位置 �Cnk�#I�oz
_%XbxP�6rH
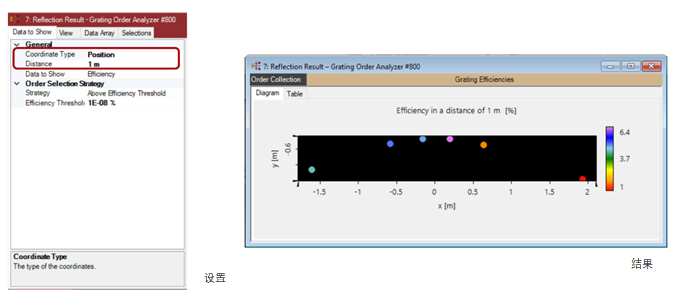 ���Xk;Uk�[ }D(DU���5r 效率vs衍射阶次笛卡尔角 ,C�N#c��o� zv&eP�q\#� ���Xk;Uk�[ }D(DU���5r 效率vs衍射阶次笛卡尔角 ,C�N#c��o� zv&eP�q\#� 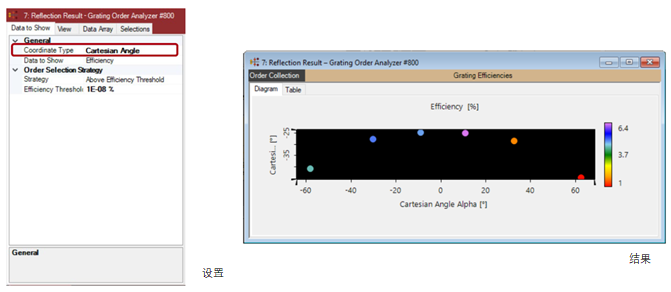 EC0��zH#�N EC0��zH#�N
|