�tp��&|*M3 在物理
光学中,我们使用麦克斯韦方程组处理电磁场。为了快速求解该方程组,我们将不同的麦克斯韦算子结合在一个非序列场追迹概念中。进一步的,快速物理光学概念的支柱是:(1)尽可能在k域求解麦克斯韦方程组。(2)根据处于哪一个场域,使用常规或几何傅里叶变换,选择k域或空间域。(3)通过所谓的双向算子
仿真光学组件的效应。(4)几何双向算子的引入。这些概念的结合产生了一种物理光学理论,其具有快速建模算法,该算法固有地以定义明确、有说服力的方式应用了几何和衍射模型。
MQ0r�l�n?� ?`�O^�;�f� 1.场追迹图 �BIe�:7cR% a�1_����o 一个
光学系统的麦克斯韦方程组的解可以通过非序列场追迹算法得到[1]。这导致所有通过系统中不同光路的
模拟,都由一系列自由空间传播步骤和与空间中非均匀区域,例如光学器件的互作用组成。从
光源平面中的场开始,自由空间算子P规定了在下一个组件平面上的场,其中组件的响应由算子B给出。这些算子应用于x域或k域。一个光路的模型可以由所谓的场追迹图说明,图1给出了相应的例子。
* >8EMq\�^ 图1 物理光学中一个光路的场追迹图模型。参数j指明了应用算子的场参考平面。 B_b�5&��M@
%*�Uc,�V�� 尽管电磁场包含六个场分量,场追
迹算法仍然可以通过ρ=(x,y),E┴(ρ,ω)=(Ex(ρ,ω), Ey(ρ,ω))正式地表示,缺失的四个分量可以根据E┴的需求计算。在k域中,这些计算遵循简单的代数方程。
+PK�siUJ|� 自由空间算子方程由 给出,输入平面场为 ,输出平面(输入平面的下一个算子)的结果为 。如果输入/输出平面不平行,则传播算子P通过衍射积分和附加的倾斜算子表示自由空间中的传播[2]。尽管在空间域中,传播被表示为有大量数值计算成本的衍射积分,但在k域中,对于平行平面和非平行平面的附加坐标变换,我们则有简单的表达式(
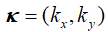
)
x.] t�G�S� 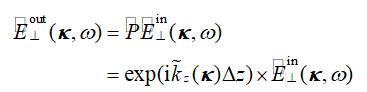
(1)
#5�'�&
|< 通过选择常规或几何傅里叶变换[3],可以来回转换k域和空间域,不同的衍射积分遵循空间域中的公式1,包括Rayleigh-Sommerfeld、远场和Debye积分。k域中自由空间传播的简单性是快速物理光学选择k域的一个重要原因。另一个原因是可以从 快速代数计算 和 。下面将介绍场追
迹算法中的B算子。
�3hUP�>�F8 �%k )H7n�j 2.双向算子 �#r�eW)P�> ?N!kYTR%}� 空间域中我们有B算子
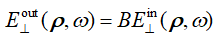
,并且类似的在k域中有
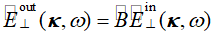
。两个域中的算子都有矩阵形式,例如k域为
�C4|OsC7J� g0��B%3�v 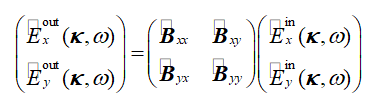
(2)
rK:cUW0]X� 这个矩阵中每一个算子都代表一个积分运算符,例如k域中有如下积分形式(忽略ω)
r�`h".=oD� �<c!gg7@pm 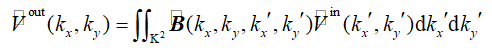
(3)
�=_ b/�g� 其中K2代表输入组件的一系列k值, V为场分量的位置标识符, B表示公式2中一个矩阵元素的积分核函数。因为(kx,ky)代表k域中传输的平面波的方向,在K2的子集中核函数
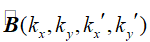
也可以被理解成方向角度的函数,说明了B是电磁场的双向散射分配函数(BSDF)的概括,尽管BSDF仅仅阐述了场能量效应。
kY{�$[+-jR �!=a]�Awr\ 图2 上图展示了正弦表面光栅中的场,通过有限元方法(FEM)计算。此外,也使用了局部平面近似(LPIA)方法计算。在下图中展示了两种方法的结果,平面中结果场的振幅标为红色。由Rui Shi提供。 �wEJzLFC�n
]�6A�w�d A 这必然被包含在了公式3中。因为BSDF的关系,我们选择 作为双向算子或者简化B算子。总的来说,计算B(k,k')和它在公式3中积分计算的应用需要大量的数值计算而且很慢。但是,在分层介质情况下,我们可以得到简化的形式
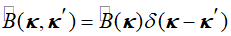
,减少了乘积的积分,并且能够快速计算k域中的算子[4]。如果我们考虑Hirchhoff边界条件下的孔径效应,空间域中算子B则变成简单的因子形式,继而我们可以在x域中通过选择合适的傅里叶变化来模拟这个效应,这在图1中通过第一个B算子解释了。当然光学的主要任务是研究电磁场传播通过两种介质间的一般表面,例如
透镜模型。
,�w�BfGpVb f#��w
u~*c 3.几何算子 25�7$�� !� �oVP��r`]� 一般表面对场的影响可以通过有限元法(FEM)来计算,但是对于大多数情况来说,数值计算成本太高。如果表面的结构不是很小,在大多数实际情况中通过所谓的局部平面近似(LPIA)方法计算B算子可以得到足够的精度[5]。在这种近似中,电磁场的边界条件利用分层介质的已知解进行局部计算。图2比较了正弦表面光栅时FMM和LPIA的计算结果,结果显示LPIA对该效应预测的很好,即使是表面上非常小的特征。事实上,我们发现LPIA是计算公式3中B(k,k')包括矢量效应(公式2)的有力手段。需要注意的是,著名的薄元近似(TEA)方法是LPIA的简化特例。尽管LPIA可以计算双向算子,我们仍然需要进行公式3中大量的数值积分计算。这导致了LPIA和几何傅里叶变换的结合[3]。如果我们假设输入场
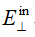
和输出场
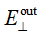
在它们的几何场域,它们遵循几何傅里叶变换理论
U/|JAg�#�� 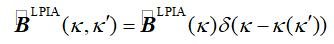
(4)
EUQtl_h/�H 公式3中的积分再一次简化为简单的乘积,其中包括了坐标变换k(k')。根据几何傅里叶变换理论,这个变换由输入场的波阵面相位计算得到。我们将公式4中的算子称为几何算子。这个结果已经于VirtualLab Fusion中实现。如果场处于其几何或衍射区域,则可以在任何平面进行数值测试。根据结果,应用了不同的傅里叶变换,也以不同的方式应用了B算子。这造成了基于纯数学论证的衍射和几何模型自然而然地应用。建模始终完全基于物理光学并在数值效率方面进行了
优化。