�=XYfzR��� VirtualLab Fusion为表面和(
光栅)区域提供了灵活的通道配置。通过调整通道配置,可以轻松实现所需的建模方案。我们以一个具有两个表面的光波导为例来演示通道的配置。通过不同的设置,我们展示了所产生的光路。此外,我们在波导面上添加光栅区域,并演示了区域的配置,以及这些区域的光栅
参数。
Nl(Aa�5:! )�JZfC&�,� 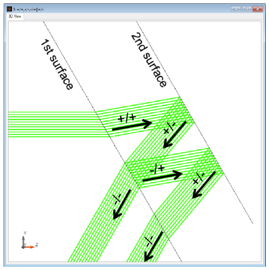 �j�m*v0kNy {�~=[�d`t� 建模任务 b�hg"�<�I *�ED�zj&��
�j�m*v0kNy {�~=[�d`t� 建模任务 b�hg"�<�I *�ED�zj&�� 如何调整表面上的通道和可能的光栅区域,以及如何用这些设置来控制
模型。
R!,�RZ�?|v 1&m0�8dZm5 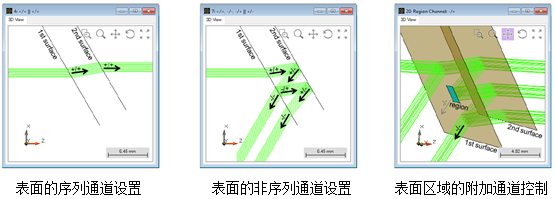 U2K>\/��-~ �\(�Hg_]>m 表面通道 �L=V��uEF� 9t)t-t#P;�
U2K>\/��-~ �\(�Hg_]>m 表面通道 �L=V��uEF� 9t)t-t#P;� 初始化
$y`|zK|�G- - 使用两个平面来
模拟石英
玻璃制成的平面光波导,厚度为5mm。
QA�LMF rWH �s�~TYzfA� 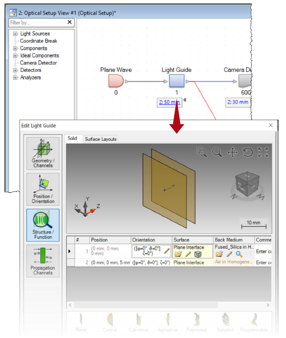 NcPzmW{#;g t��w.%'oJ7 表面通道 �M���,�<%j m�@yaF:
�R
NcPzmW{#;g t��w.%'oJ7 表面通道 �M���,�<%j m�@yaF:
�R 初始化
P��l �5+Oo - 使用两个平面来模拟石英玻璃制成的平面光波导,厚度为5mm。
�mT~:k}u~W - 为了更好地说明问题,为波导定义一个独立的Y轴旋转30°。
1r�a�}�^H} y�hTe*I=Gk 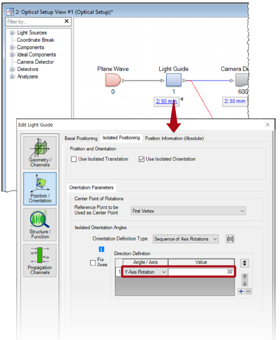 |"���ck;.) 2Gx&E�C�a, �<iTaJa$0m 表面通道 �8�IVKS>�� w%L0mH2]ng
|"���ck;.) 2Gx&E�C�a, �<iTaJa$0m 表面通道 �8�IVKS>�� w%L0mH2]ng 通道定义
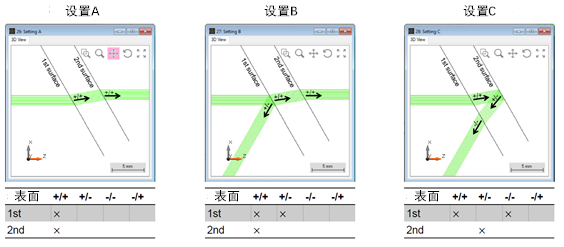
()P�?f�e�d - 每个表面有四个可能的通道,至少要激活一个通道进行追迹。
9@��^/ON\O - 可以为每个表面单独定义通道。
c !5�OK4+Z - 通道的不同设置会导致不同的建模方案。
�9}"�:�}!� 9m�8`4%�y=  ^D6�Jc�k�W ���{)`5*sd 表面通道 _tY�t<oB~%
^D6�Jc�k�W ���{)`5*sd 表面通道 _tY�t<oB~%
�?�SS?�I�
 V�g2s~�ce{ |>p\�*Dl}H 表面通道 k�R'!��;}s ZL-@2ZU{�1
V�g2s~�ce{ |>p\�*Dl}H 表面通道 k�R'!��;}s ZL-@2ZU{�1 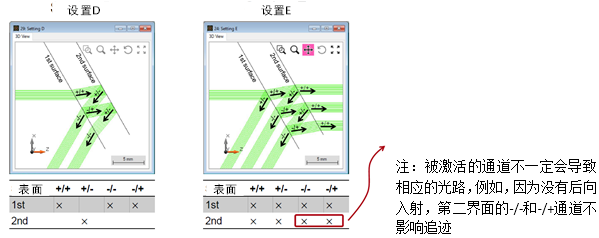 �YwKY�3�kL f9#B(4Tg�i 区域通道 X, J.!:�4` =`{!�"� 6a
�YwKY�3�kL f9#B(4Tg�i 区域通道 X, J.!:�4` =`{!�"� 6a 表面上的区域
��`3�3+OW -可以在表面上定义单个区域,并单独定义其
光学特性,包括通道设置。
|~'{ [?�a* Oa*/jZj�r� 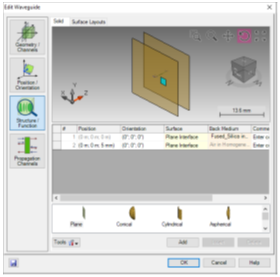 0W�Q0-~wx� 5vY1 XZ�t{ 区域通道 f�v�)-o&Q# l&E-��H@Pe
0W�Q0-~wx� 5vY1 XZ�t{ 区域通道 f�v�)-o&Q# l&E-��H@Pe 区域定义
jb7�7�uH_ -在第一面建立一个长方形区域。
)%)�?��M
* -设置区域大小为2.25 mm×2.25 mm,中心沿x方向为-3.6 mm。
;)UZT^f`)K eZ�f-i1l�J 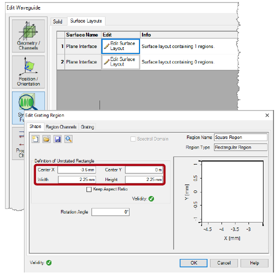 K�f(% aDYq Oq|pd7fcgm 区域通道 Lw-�)ijBW� =�Ty�N"0@�
K�f(% aDYq Oq|pd7fcgm 区域通道 Lw-�)ijBW� =�Ty�N"0@� 区域定义
|f`�!�{�=? -在第一面建立一个长方形区域。
(swP�#�t5S -设置区域大小为2.25 mm×2.25 mm,中心沿x方向为-3.6 mm。
�#{<�Jm?sU -将此区域定义为具有单一透射系数T0 = 50%的光栅,和单一反射系数R0 = 50%的光栅,这就构成了一个半
反射镜。
v�sLn�@k3 -在这里,我们只使用零次
衍射阶,这与通常的透射或折射引起的反射是相同的。
� [�NJ!�� pNE!waR��> 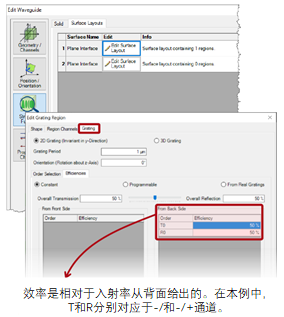 � �c~dX8+ Pbz-I3�+66 区域通道 Rqu�;;�VI[
� �c~dX8+ Pbz-I3�+66 区域通道 Rqu�;;�VI[ 区域定义
Avh�mN5O�= - 按照与表面相同的规则,为这个区域设置通道。
y?Fh%%uNr� �u9'4q<>&� 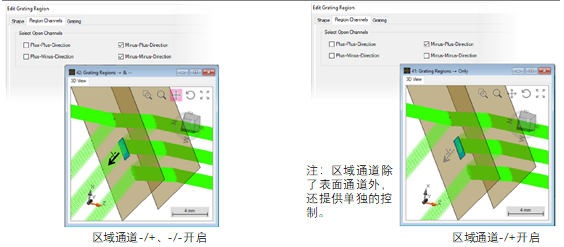 �2D&t��DX< �1�jQz%^�~ 带有光栅的区域通道 p`X�I�(�NI H@O�YtPHGR
�2D&t��DX< �1�jQz%^�~ 带有光栅的区域通道 p`X�I�(�NI H@O�YtPHGR 区域定义
u�:f�ii�l$ - 可以在给定区域上定义一个衍射光栅。
RYmk�6w�!w �S1z�V.]�� 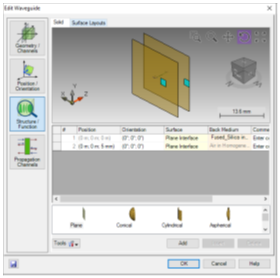 �1\_4# @') �"��jb�?P$ 带有光栅的区域通道 0I079f�qk< sL[,J[A�N;
�1\_4# @') �"��jb�?P$ 带有光栅的区域通道 0I079f�qk< sL[,J[A�N; 区域定义
�1<pbO:r� -可以在给定区域内定义一个衍射光栅。
HOXqIZN85� -我们在第二表面上增加一个矩形区域(侧长2.25mm),沿x方向以-8.2mm为中心。
Uj�b�||�(W `P�"-9Ue�= 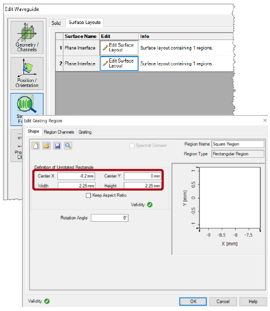 b\��H~Ot[i Mx[tE?!�2 带有光栅的区域通道 /q(+r5�k \ Rl<~:,�D
b\��H~Ot[i Mx[tE?!�2 带有光栅的区域通道 /q(+r5�k \ Rl<~:,�D
区域定义
BDc*N]m}B1 -可以在给定区域内定义一个衍射光栅。
]��J�m�9D= -我们在第二表面上增加一个矩形区域(侧长2.25mm),沿x方向以-8.2mm为中心。
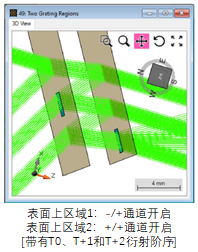
�4z?6�[Cg< -定义一个2微米周期的理想光栅,指定的衍射系数为:
N��C�X�!ss T0=10%
tU�L�(1:-C T+1=60%
�l��$�MX�\ T+2=10%
T3!l{vG
\O e)>Z&e,��3 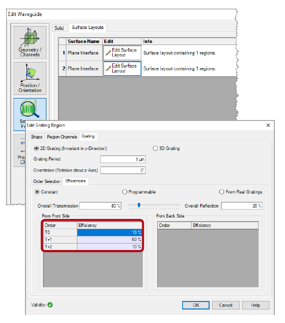 bV`�Z�o�(z ,SS@]9A��& 带有光栅的区域通道 =as��]>�?< t$rWE|+_z�
bV`�Z�o�(z ,SS@]9A��& 带有光栅的区域通道 =as��]>�?< t$rWE|+_z� 区域定义
�8[��
:FU� -可以在给定区域内定义一个衍射光栅。
p}O@�%*p�. -我们在第二表面上增加一个矩形区域(侧长2.25mm),沿x方向以8.2mm为中心。
7$;mkHu4H% -定义一个2微米周期的理想光栅,指定的衍射系数为:
ka*VQ��Xk* T0=10%
X~�%Wg*H�m T+1=60%
T?NwS�xGo T+2=10%
lv�,8NmP5� �vpTS>!�i�