W1!eY,1} 0=5i\*5 p
5 O6MI4: LtU+w*Gj 由于相位和
结构之间的直接关系，
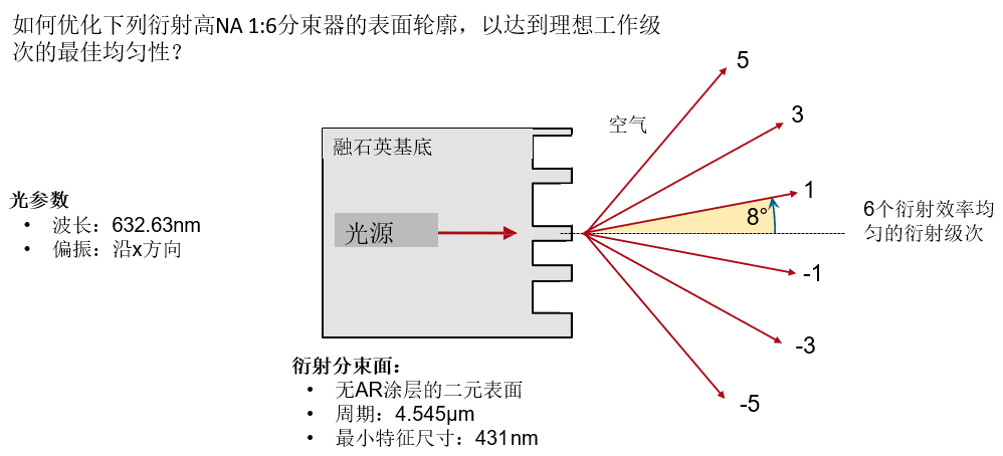
衍射分束镜通常采用一定的傍轴近似来设计，这些算法也提供了这种近似，反之亦然。在非傍轴或甚至高NA分束器的情况下，这些近似将引入一些不准确性，因此，如果不进行额外严格的后
优化，至少建议进行严格的分析。在这个用例中，使用奇数衍射级对典型的二元1:6分束器执行这样严格的评估。为此，对初始
系统的结构进行了
参数化，并通过可编程
光栅分析器定义了一组自定义的评价函数。对于参数优化和后续的公差分析，使用严格的傅里叶模态法 (FMM)。
.iS ]aJJ *&PgDAQ 建模任务 1k~jVC2VA
<|_Ey)1
6
A^Zs?<C- \mDm *UuG
衍射分束面初始设计(*) avz 4 &
ie ,{C
;'Q{ ywr GkC88l9z 1. 采用VirtualLab Fusion的迭代傅里叶变换算法(IFTA)设计工具计算了分束器的初始相位函数。
=@z"k'Vl` 2. 对于高度轮廓的转换，采用了基于薄元件近似(TEA)的结构设计。
C;ye%&g> zKutx6=aj (*)不是这个用例的一部分 (**)这些会话编辑器在衍射
光学工具箱银版中可用。
>6dgf`U Mzd}9x $'J TEA和等距抽样结构的局限性 [K KoEZ
t(yv
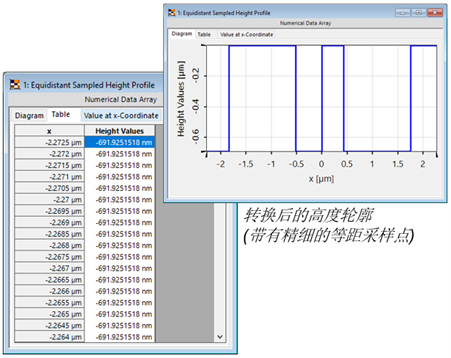
p[eRK .$! xle29:?l TEA非常适合于最小特征尺寸不小于约5倍
波长的情况。如果不是这样，振幅/相位分布与设计高度轮廓相互作用后可能会显示出与期望值的相关偏差。
X<{m;T ` 因此，需要进行严格的评估。
'YeJGzsJp 对于参数优化，需要对结构数据进行不同的定义。
q ^gEA5 z W _'sC 后优化的数据准备(参数化) AK!G#u g !v`=EF .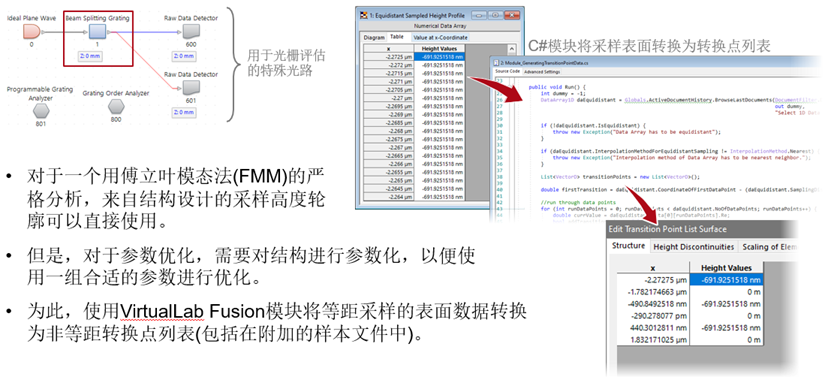 
IviWS84 U_~~ PCi 衍射分束器表面进一步优化 )/JC.d#
#n"/9%35f`
'$zFGq
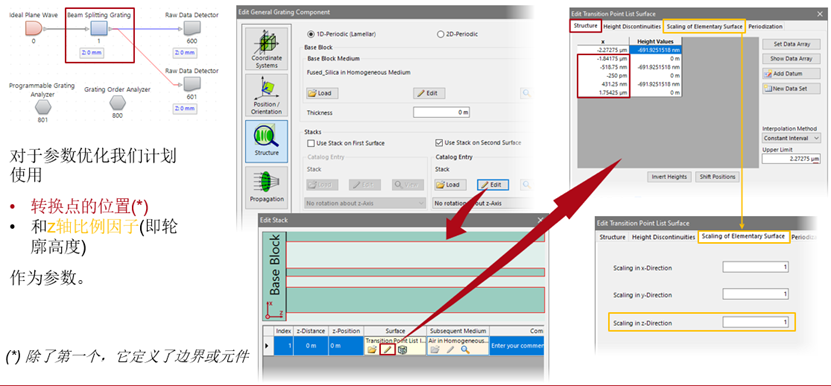
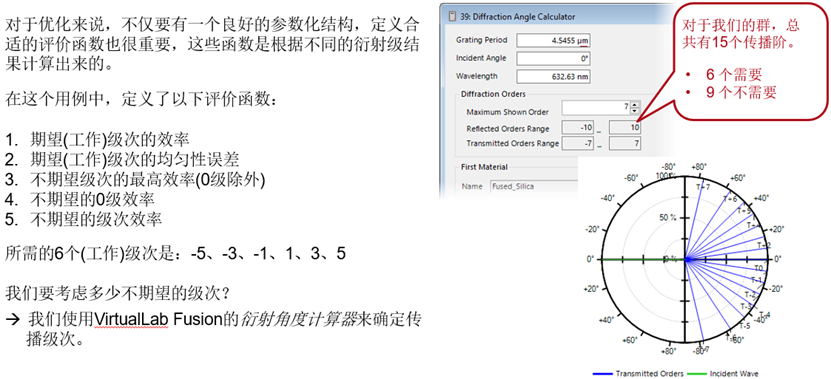
}} ^n]s}t}csV 哪个衍射级次有哪些评价函数？ !jbjrzv9
>gE_?%a[
9s)oC$\ Bz{
g4!ku 利用可编程光栅分析器 D4|_?O3 |m
'zb7:[[7%
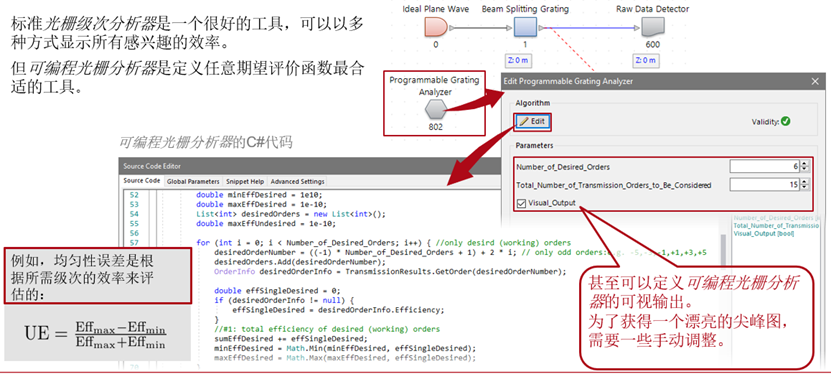4l*&3Ar 7,zARWB!? 分束器初始设计的严格分析
ZS+2.)A
f/x "yUq
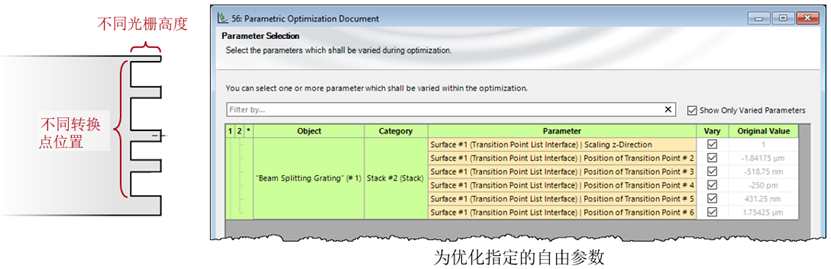
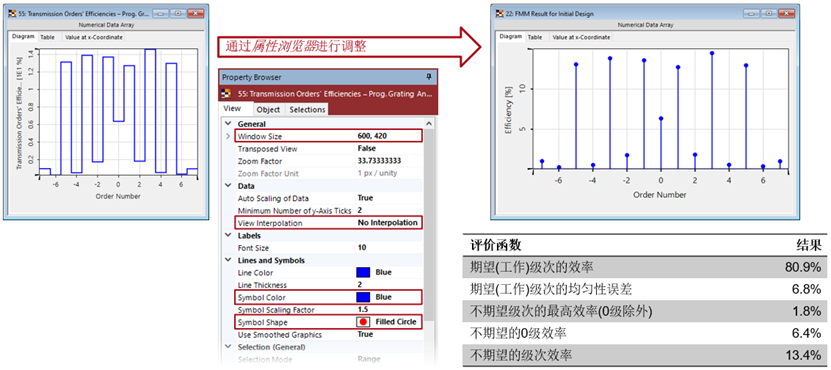_bi Jch UPYM~c+} 设置优化参数 }0(
Na
X`b5h}c
#<o#kJL 7E95" B&w 两个优化过程对比 NP8TF*5V 在这个用例中，我们演示了两种具有不同配置目标和约束的优化：
PwW @I~@> 在优化#1中，优先考虑均匀性误差。
)R4<*
/C:w 在优化#2中，0级也要最小化。
) YFs 
KB = z{g 关于评价函数约束，用户可以指定
W<Lrfo&=Y] 单独的目标值、范围、下限或上限是什么
5o/rV.I 以及通过权重，它们的贡献应该是什么。
Pa}vmn1$ 
? la_ +;m 在优化过程中，采用了内建的下降单纯形算法
Eg*3**gTO b5Pn|5AVj 评价函数约束的配置 MQ44uH J
SOmn2
}
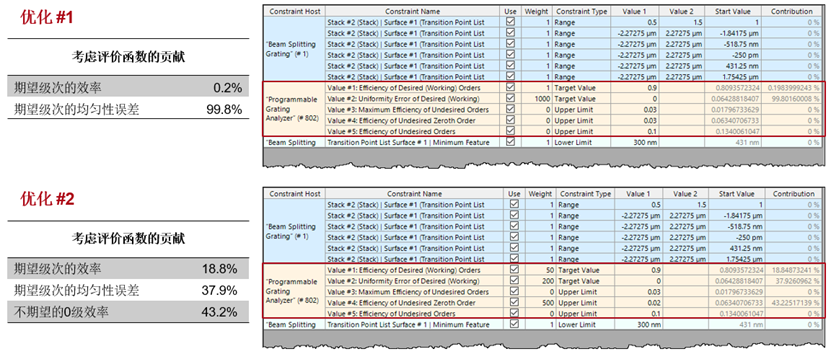7,TWCVap G$ FBx 优化#1(优先级=均匀性误差) o3=kF
`?x$J
6p
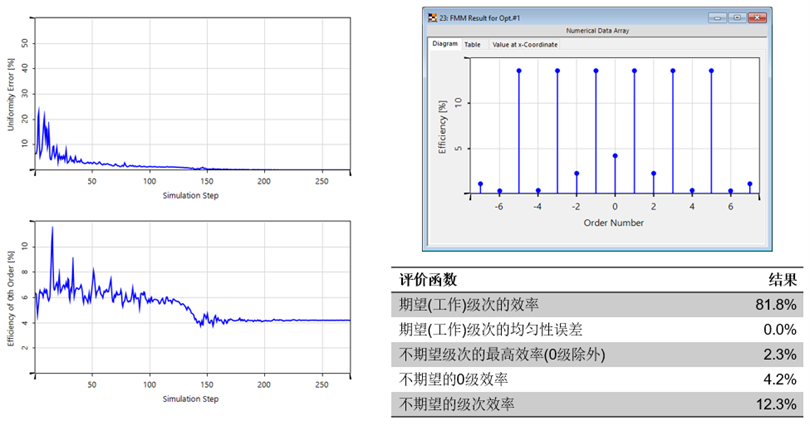8GldVn.u PS6`o 优化#2(优先级=均匀性误差&低0级) J~q+ G
919g5f`
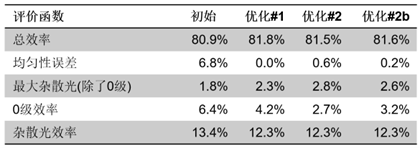
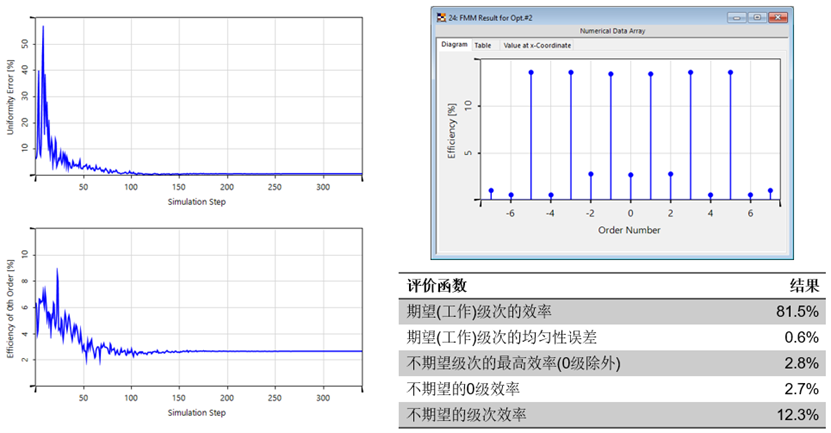` qTY [Jo TWouNU 严格结果对比(初始—优化#1—优化#2) UsN b&aue
>{a,]q*
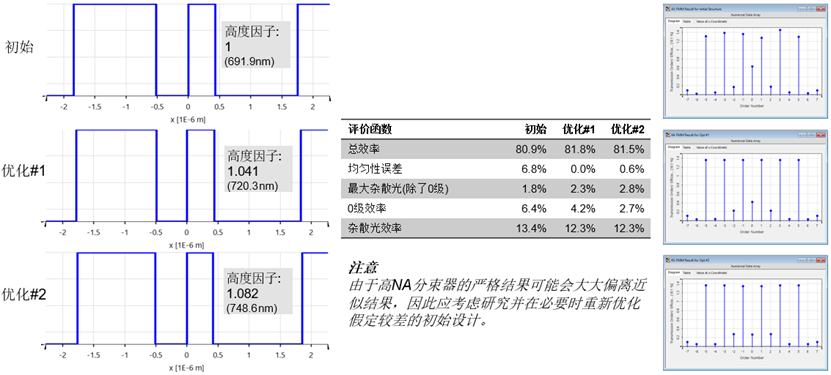aB^ G _GqE'VX 公差仿真结果 \]xYV}(FO
U[l%oLra
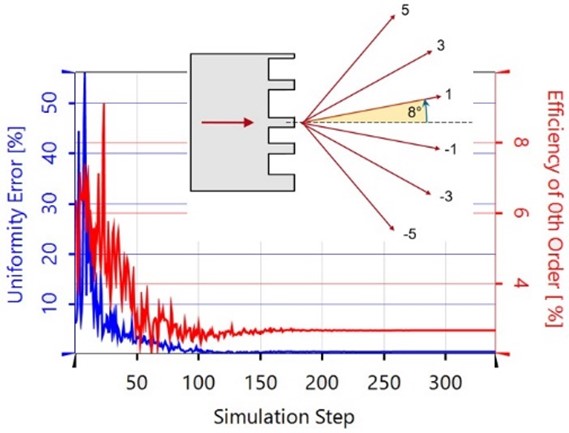
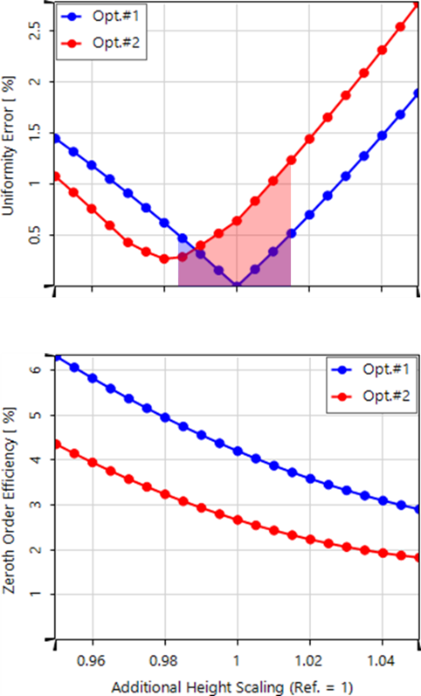
wVDB?gy%# E,7~k d~y` 研究了在±5%范围内生产过程中可能的高度公差时质量函数的表现。
jm\#($gl= 在大部分的公差范围内，蚀刻深度误差约为±1.5%(蓝色&红色区域长度)，第二种优化设计的均匀性明显较差。
LltguNM$ 乍一看，优化#2的最小均匀性误差(红色曲线@0%)并不居中，这似乎有些奇怪。这是因为优化#2优先考虑了低0级效率，从而牺牲了一些均匀性来实现这一目标。
9eiBj 因此，对于公差分析的整个预期范围，第2种优化的结构总是有一个明显较低的0阶。
Wg^cj:&`u 注意：
de9l;zF 公差仿真结果中的参考值1总是指被检测结构的各自单独优化高度(用紫色线表示)。
Z@!W? Ed u9w&q^0dqG 公差仿真结论 v\,%)Z/
AF]!wUKxy
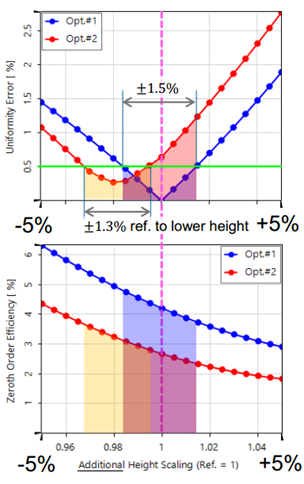
2p>SB/ 公差测试提供了一个更好的信息基础，以决定什么是最适合所需应用的结构。
Q/)o k$A& 可以看出，如果使用均匀度误差最低的高度，在相似的±1.3%(黄色区域长度)的公差范围内，第2次优化的结构均匀度误差低于0.5%(绿线)。
on?/ tHys 因此，具有 0.9825 (707.7 nm) 额外高度缩放的第二次优化结果可能是一个具有整体性能合适的良好解决方案。在下表的最后一列“优化#2b”中显示了相应的结果。
4/?}xD|? w9$8t 9$| 
