[技术]Savitzky-Golay滤波函数 [复制链接]

H(15vlOD  
j:3EpD@GS  
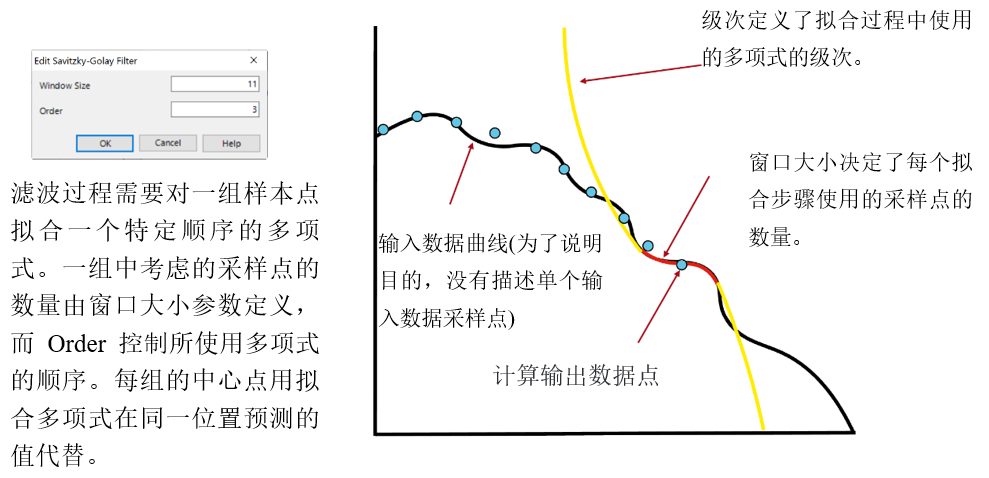
在测量信号或数据的情况下，很难(如果不是不可能的话)完全避免所有可能的噪声源，因为这些噪声源会干扰任何实验测量。但是，噪声的存在会干扰数据的重要特征(例如，测量光谱的半宽谱)。 L1hD}J'$4  
        因此，有一些后期处理技巧可能会有所帮助。这里我们只讨论一个这样的工具:Savitzky-Golay滤波器，它通过对一组采样点执行回归算法来平滑局部噪声。在这个例子中，我们讨论了VirtualLab Fusion中这个特性的选项和效果，并以一个绿色LED灯在60 nm带宽下发射的光谱为例进行了测试。 PwW^y#96  
,`<^F:xl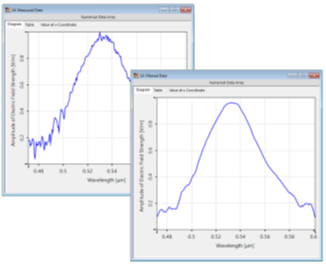  
>`7OcjLg  
e'1 ^+*bU  
2.如何进入Savitzky-Golay过滤器 >|a\>UgC  
-3.UE^W2  
 3L%WVCB  
        对于每个实值数据数组，都可以在下面找到Savitzky-Golay滤波器 g/IH|Z=A  
        操作→ V@vhj R4r\  
杂项→ #)GW}U]X  
        Savitzky-Golay过滤器 f}[H `OF  
@Ex;9F,Q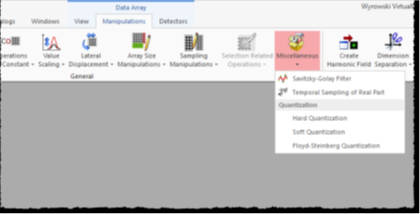  
cz2,",+~  
-a *NbH  
3.可视化的过滤函数 4~O6$;!|~  
\ V6   
^ED"rMI  
0iYP  
4.影响过滤器-窗口大小 :T_'
n,  
%_R$K#T^,  
更大的窗口大小导致在拟合过程中考虑更多的采样点，因此曲线更平滑。 $ZQ"({<w<g  
ispkj'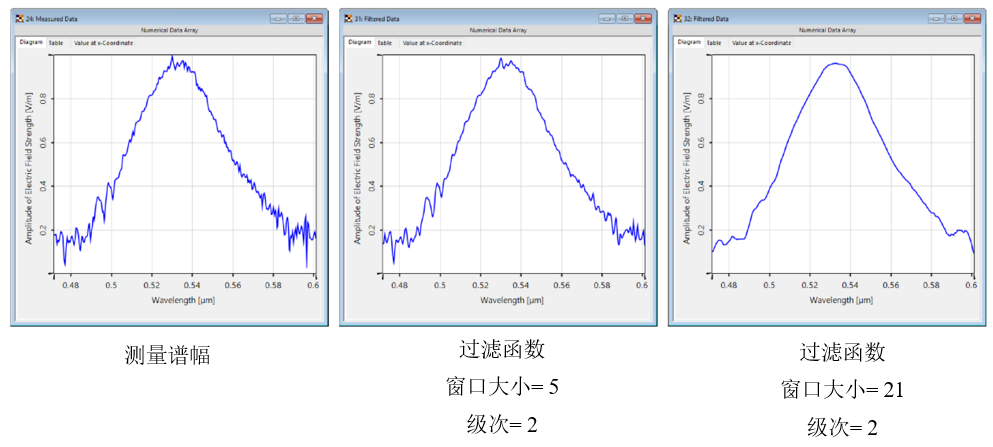  
pT4qPta,2  
FZiZg;  
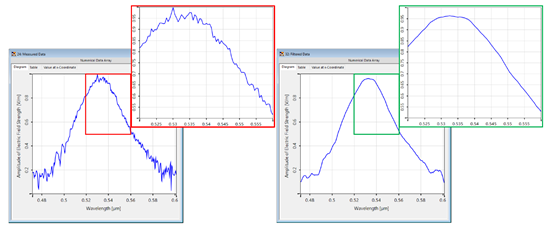
更高的阶数允许更详细的曲线，但反过来也可以保留局部噪声。 ^:qD.h>&  
!w q4EV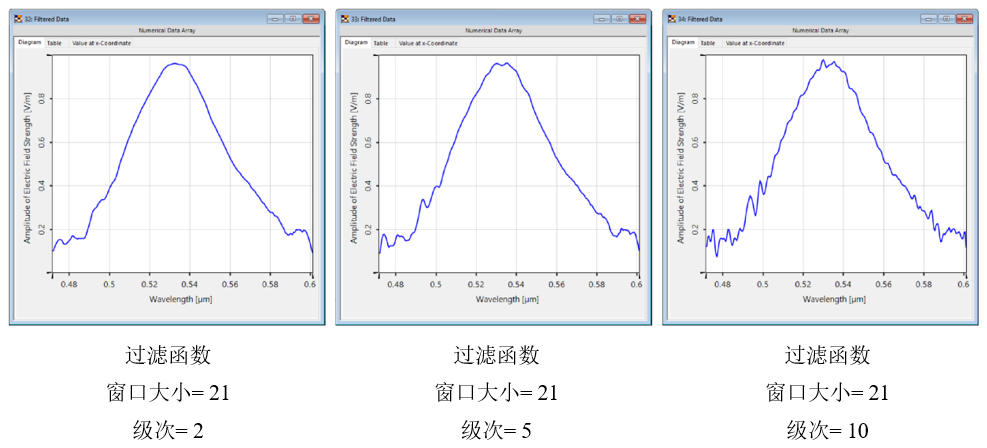  
RCI4~q  
|~SE"  
5.局部噪声过滤 R6`*4zS  
np\st7&f6  
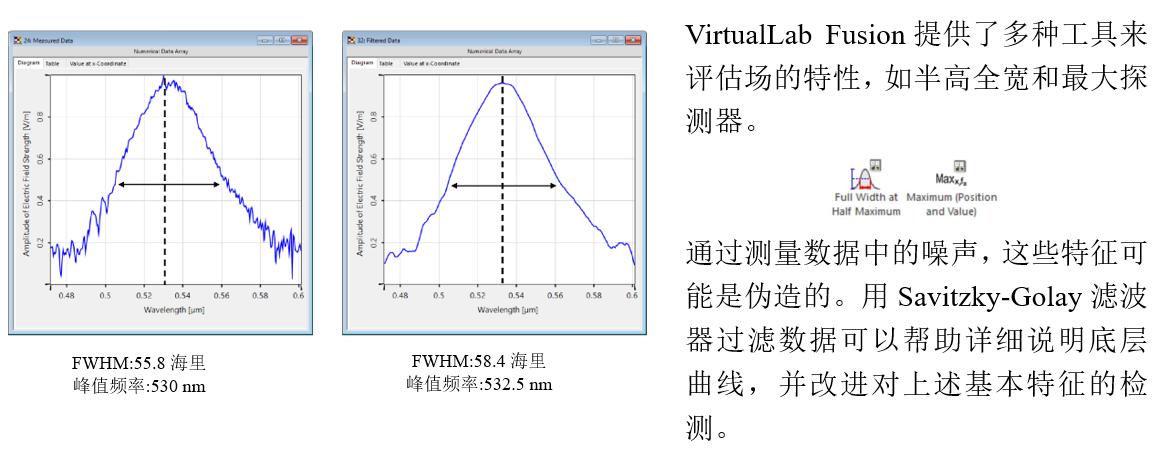
?*[\UC  
DU;[btK>  
6.FWHM 检测 %c]nWR+/  
oEJaH  
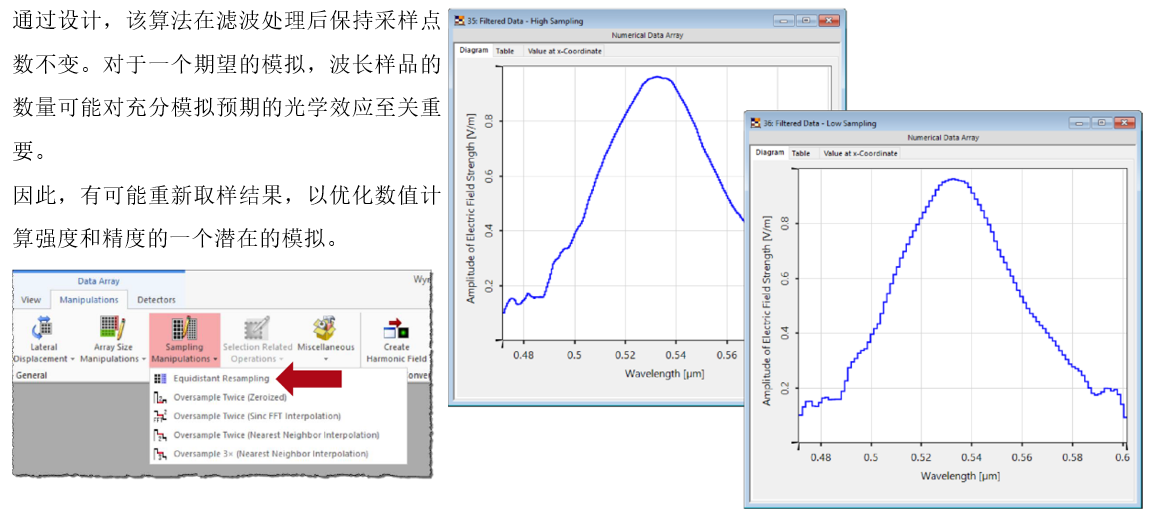
tpXa*6  
i;c'P}[K  
7.等距的重采样 rFo\+//  
UP\C"\