-
UID:317649
-
- 注册时间2020-06-19
- 最后登录2026-02-11
- 在线时间1927小时
-
-
访问TA的空间加好友用道具

|
谐振波导光栅(RWG)由于其在波长、相位和偏振等方面的可调谐性,在研究和工业中有着广泛的应用。RWG的结构包含一个薄的高折射率波导薄膜,该薄膜与光栅接触。波导支持多种导模,并且根据厚度的不同,模式的数量也不同。在这个例子中,我们应用VirtualLab Fusion中的傅立叶模态法(FMM)严格分析RWG的性质。 +�*a7�GttU
�o?�dR\cxj
 o<�J5����! �*�w 21U!� 建模任务 'w6hW�7"L� o<�J5����! �*�w 21U!� 建模任务 'w6hW�7"L�
T6=-hA^��A
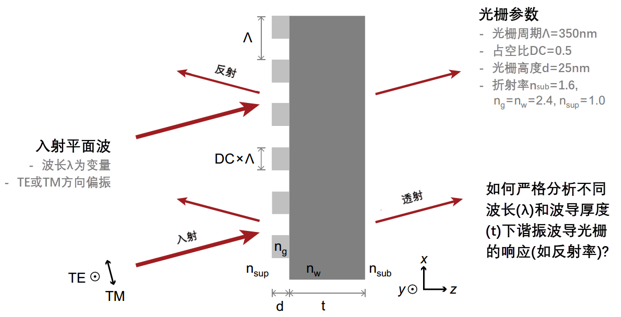 g)cY\`�&W8 �Omb.�53+� 不同波长和厚度的反射率 KZ3�B~#oQ� g)cY\`�&W8 �Omb.�53+� 不同波长和厚度的反射率 KZ3�B~#oQ�
� tgW�� kX
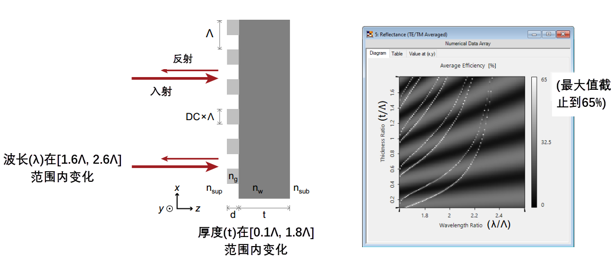 cz��S7-Hh@ +2y&B,L_Wh 不同波长和厚度的反射率 G�Z�"/k<~0 cz��S7-Hh@ +2y&B,L_Wh 不同波长和厚度的反射率 G�Z�"/k<~0
NL-_#N$��� 仿真结果来自参考文献: 8^�T2^�g�s G. Quaranta, G. Basset, O. J. F. Martin, and B. Gallinet, Laser & Photonics Reviews 2018, 12, 1800017. [Fig. 3 a) gvo?([j-m�
���-fPT}v�
VirtualLab Fusion的仿真结果 ai�^t�=�
s
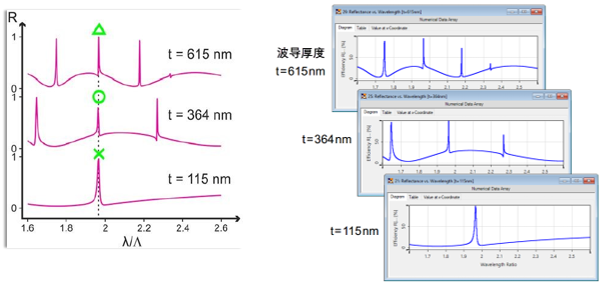
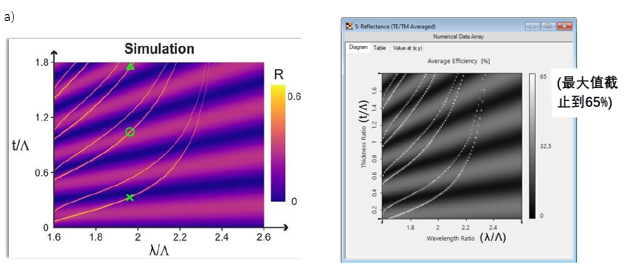 LE|��<O��� 特定波导厚度的反射率 ' =�}pxyg� LE|��<O��� 特定波导厚度的反射率 ' =�}pxyg�
Y�kI9d&ib+
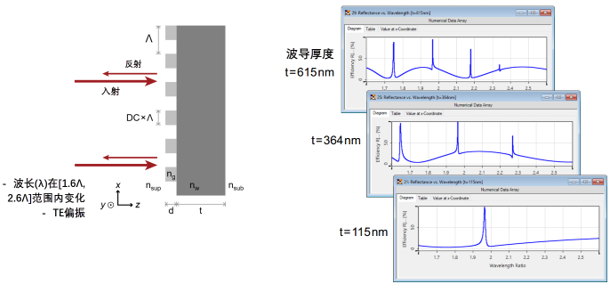 ���~�me\�� ucM.Ro=@�� 特定波导厚度的反射率 )JX$/-
RD- ���~�me\�� ucM.Ro=@�� 特定波导厚度的反射率 )JX$/-
RD-
�B�_tQeM� 仿真结果来自参考文献: +�!xu{2�! G. Quaranta, G. Basset, O. J. F. Martin, and B. Gallinet, Laser & Photonics Reviews 2018, 12, 1800017. [Fig. 3 c) kF�2Qv�.5! ��['�t8�C�
VirtualLab Fusion的仿真结果 sMX�$�Q45e
]b�)!YP�o�
 U�2UyN9:6F 谐振模式可视化(@λ = 687 nm) 0Jg+�s�Us{ �4y>(RrVG� U�2UyN9:6F 谐振模式可视化(@λ = 687 nm) 0Jg+�s�Us{ �4y>(RrVG� 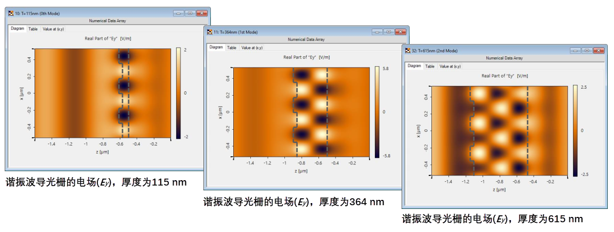 P4[]q�bfd, P4[]q�bfd,
BPiiexTV9 角灵敏度分析(t = 364 nm @λ = 632.8 nm) GoL|i�NW�` @E(P9zQ/zy  yDuq6�`R* �7@@�<5&mN 用聚焦高斯光束检验共振效应 � �z�� �\^ �����<
G�U yDuq6�`R* �7@@�<5&mN 用聚焦高斯光束检验共振效应 � �z�� �\^ �����<
G�U 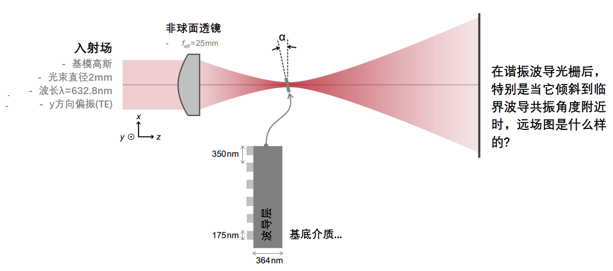 |Q6h�/"��2 |Q6h�/"��2
%�G�VN4y�& 用聚焦高斯光束检验共振效应 sL��8>GtVo 2_.��CX(kI 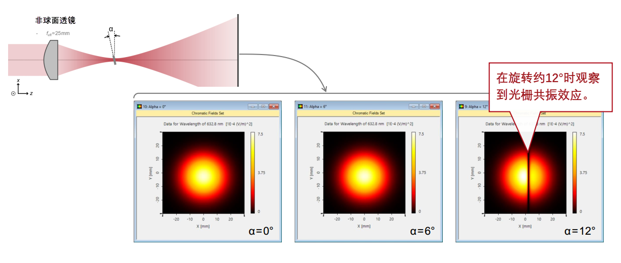 h[,�Xem�wX h[,�Xem�wX
#@q1Ko!NZ 用聚焦高斯光束检验共振效应 <K,[sy�&Qy :ovt?q8"> 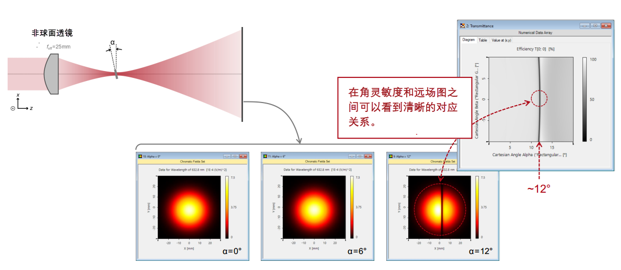 �w_�!%'9m>
Z:�T�FOnJ 走进VirtualLab Fusion �)���WclV~ �w_�!%'9m>
Z:�T�FOnJ 走进VirtualLab Fusion �)���WclV~
F��Nlx1U[�
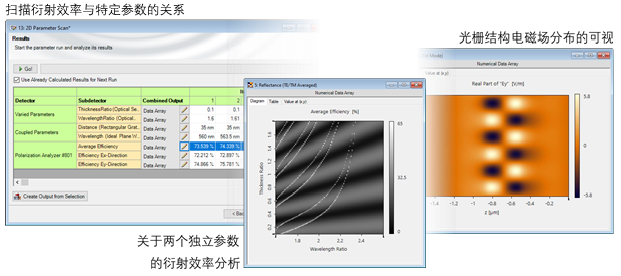 Exq�M1&zpK K?�JV]�^� VirtualLab Fusion的工作流程 01o [!n��T Exq�M1&zpK K?�JV]�^� VirtualLab Fusion的工作流程 01o [!n��T
+8e�V�j#�N 构建光栅结构 �t��b�S#^Y - 利用界面构建光栅结构 [用例] Yu�;9&���b - 利用特殊介质构建光栅结构 [用例] _^�-D� _y� e�N4t�1��$ 分析光栅衍射效率 [lZ=s�[n.� - 光栅级次分析器 [用例] �]h0Y8kp�d U�(!?d ]en 通过参数运行检查不同参数的影响 ��{F/q{c~] - 参数运行文件的使用 [用例] �xjE7D�CmA K,]�woNxaw 计算光栅结构内的场 <oQ6��Z��X
�+�2El� �
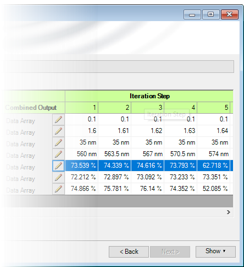 s�X
Z4U0�# Gg}t-�_��M VirtualLab Fusion技术 0a@c/�XGBp ,��,�7.�=# s�X
Z4U0�# Gg}t-�_��M VirtualLab Fusion技术 0a@c/�XGBp ,��,�7.�=#
 N?z�V*ngBS N?z�V*ngBS
|