-
UID:317649
-
- 注册时间2020-06-19
- 最后登录2025-12-12
- 在线时间1894小时
-
-
访问TA的空间加好友用道具

|
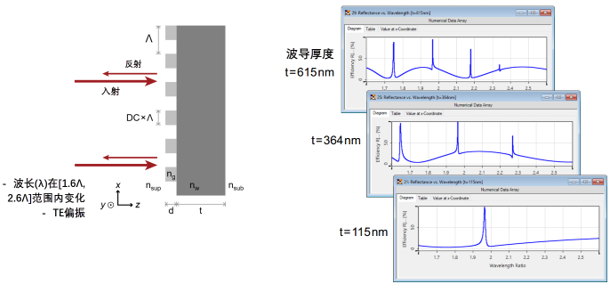
谐振波导光栅(RWG)由于其在波长、相位和偏振等方面的可调谐性,在研究和工业中有着广泛的应用。RWG的结构包含一个薄的高折射率波导薄膜,该薄膜与光栅接触。波导支持多种导模,并且根据厚度的不同,模式的数量也不同。在这个例子中,我们应用VirtualLab Fusion中的傅立叶模态法(FMM)严格分析RWG的性质。 [�@m[�V1D�
F:%�^&�%\�
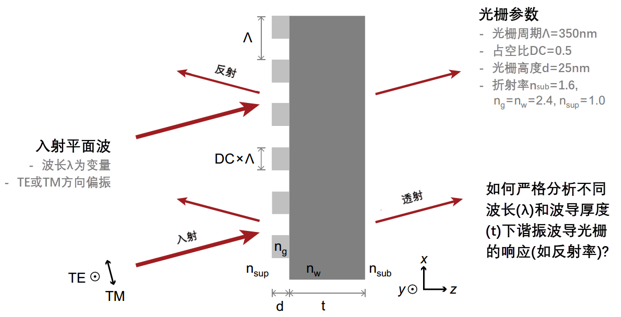
 )YuRjBcp," NSw�<t9�Yi 建模任务 K7IyC��cdB )YuRjBcp," NSw�<t9�Yi 建模任务 K7IyC��cdB
T yU&�Q�Xb
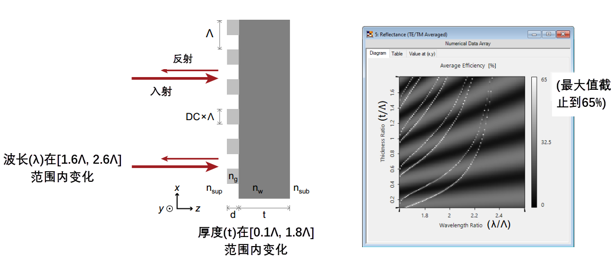
 _6����;<ow ��N�B E�pM 不同波长和厚度的反射率 n0_B�(997* _6����;<ow ��N�B E�pM 不同波长和厚度的反射率 n0_B�(997*
_�u>�t3RUA
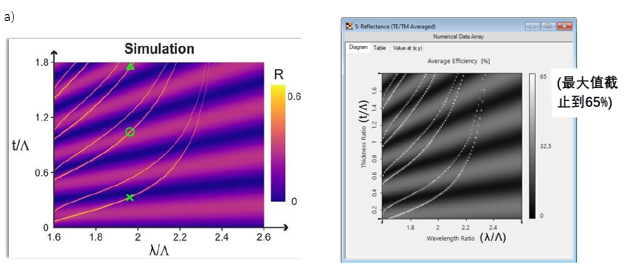
 ajW[�e�yX� xE%O:a?�S� 不同波长和厚度的反射率
jm[�}M��� ajW[�e�yX� xE%O:a?�S� 不同波长和厚度的反射率
jm[�}M���
/H')�~!�Yz 仿真结果来自参考文献: Bwj�g#1�E G. Quaranta, G. Basset, O. J. F. Martin, and B. Gallinet, Laser & Photonics Reviews 2018, 12, 1800017. [Fig. 3 a) tG/a�H%�4S
8�QV t,
'I
VirtualLab Fusion的仿真结果 O -�G1})$
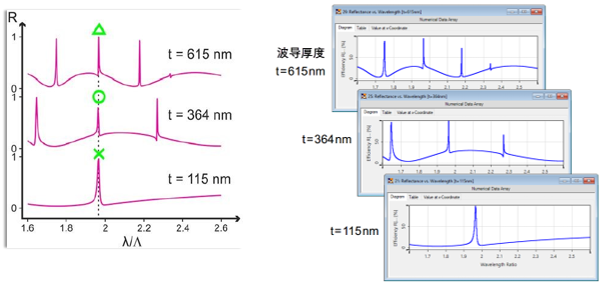
 �D�9~}5��� 特定波导厚度的反射率 Rab#7Q16Q8 �D�9~}5��� 特定波导厚度的反射率 Rab#7Q16Q8
Y�2<dM/b/�
 tW�m>����j tJ"�az=�?� 特定波导厚度的反射率 �`h?LVD�'l tW�m>����j tJ"�az=�?� 特定波导厚度的反射率 �`h?LVD�'l
UxyY<H~W�x 仿真结果来自参考文献: H�OfF"QAR$ G. Quaranta, G. Basset, O. J. F. Martin, and B. Gallinet, Laser & Photonics Reviews 2018, 12, 1800017. [Fig. 3 c) zL���P],wB 'Q5�&5UrBr
VirtualLab Fusion的仿真结果 KxY$�Pg�cC
Jy�9��b��Y
 R*087X7
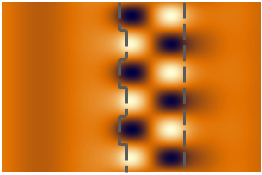
N| 谐振模式可视化(@λ = 687 nm) c1�5r':.�5 QZ&�4:K+�{ R*087X7
N| 谐振模式可视化(@λ = 687 nm) c1�5r':.�5 QZ&�4:K+�{ 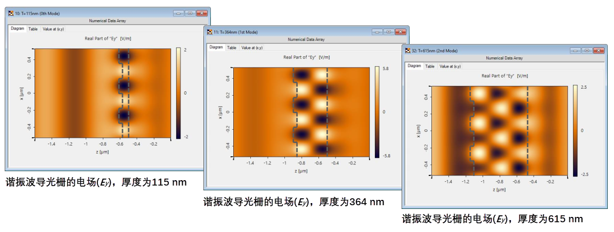 <
�kz[:�n: <
�kz[:�n:
+P�|�2m"UA 角灵敏度分析(t = 364 nm @λ = 632.8 nm) <;%0T
xK|U �iNQ0p:�<k  a5a1'IV�q� �{7qA�&�c= 用聚焦高斯光束检验共振效应 =L"�^.c�@� �i�bXe"X/_ a5a1'IV�q� �{7qA�&�c= 用聚焦高斯光束检验共振效应 =L"�^.c�@� �i�bXe"X/_ 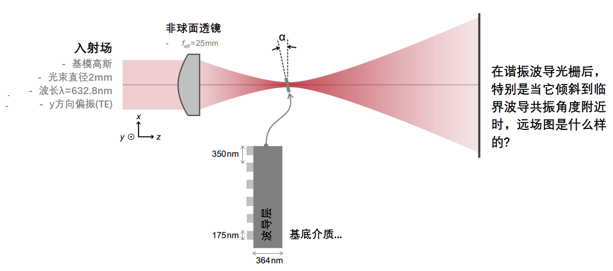 :�j@8L.<�U :�j@8L.<�U
-ui�<�E?v 用聚焦高斯光束检验共振效应 [�(|^O>k8c �GB>aT-G7q 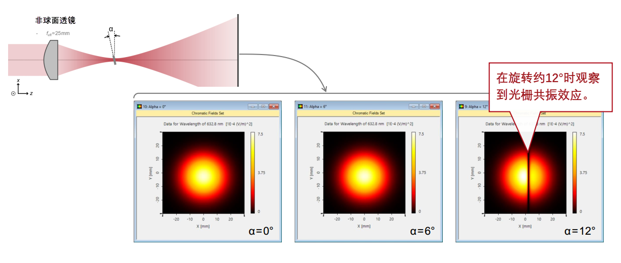 tjj^O%SV<� tjj^O%SV<�
P�/MM
U�mO 用聚焦高斯光束检验共振效应 If;R?j�0;Q :6P��nie�� 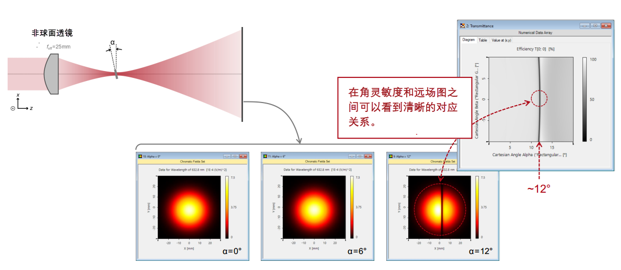 �`}�gdN}�; zI^Da!��r. 走进VirtualLab Fusion dv�, C6t2 �`}�gdN}�; zI^Da!��r. 走进VirtualLab Fusion dv�, C6t2
e0 u,zg�+m
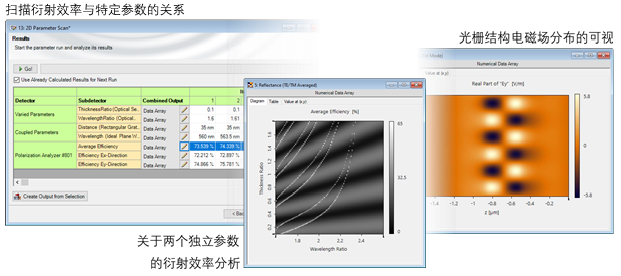 n_P��3\Y|� �b�#/i.!:a VirtualLab Fusion的工作流程 ^O)�v��e^P n_P��3\Y|� �b�#/i.!:a VirtualLab Fusion的工作流程 ^O)�v��e^P
%&+TbDE+T 构建光栅结构 0I�����5&a - 利用界面构建光栅结构 [用例] ��-f?�A��h - 利用特殊介质构建光栅结构 [用例] V�YaS�B?`/ ;wR� '�z$8 分析光栅衍射效率 �Q`A6(y/s? - 光栅级次分析器 [用例] cwe1^SJ�6y .'1SZ�e�7O 通过参数运行检查不同参数的影响 �|CIC�$�2u - 参数运行文件的使用 [用例] '���eyJS`
�pjw��a�L^ 计算光栅结构内的场 �EB!daZH,
�[
]�^X`�R
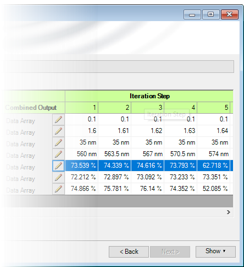 �ka/XK[/�' 'e�@=^F�C VirtualLab Fusion技术 �}mZV�L~|V }H�RK?.Vj: �ka/XK[/�' 'e�@=^F�C VirtualLab Fusion技术 �}mZV�L~|V }H�RK?.Vj:
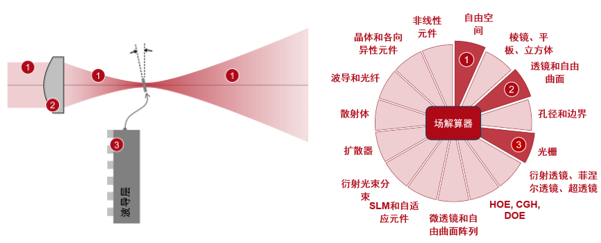 O>�c$s�L0g O>�c$s�L0g
|