-
UID:317649
-
- 注册时间2020-06-19
- 最后登录2026-02-11
- 在线时间1927小时
-
-
访问TA的空间加好友用道具

|
谐振波导光栅(RWG)由于其在波长、相位和偏振等方面的可调谐性,在研究和工业中有着广泛的应用。RWG的结构包含一个薄的高折射率波导薄膜,该薄膜与光栅接触。波导支持多种导模,并且根据厚度的不同,模式的数量也不同。在这个例子中,我们应用VirtualLab Fusion中的傅立叶模态法(FMM)严格分析RWG的性质。 !3v"7l{LF�
s(9rBDoY(8
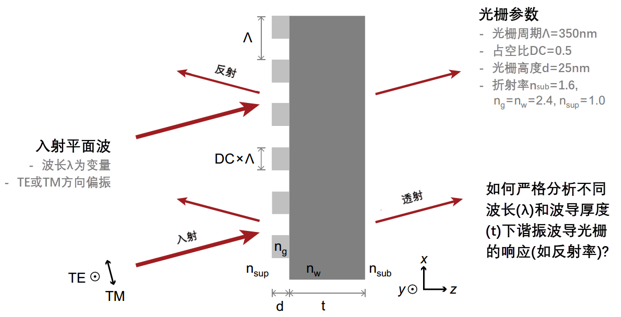
 2�EcY�O$R! D>^ix[:J� 建模任务 !!��#ale�& 2�EcY�O$R! D>^ix[:J� 建模任务 !!��#ale�&
R�[��-�:-8
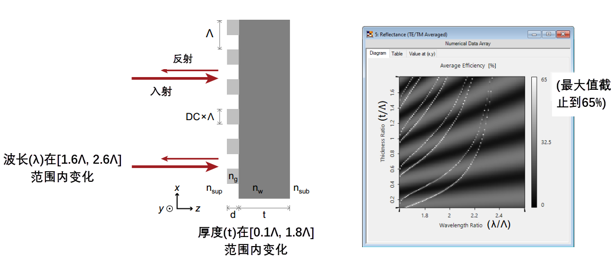
 w%�-!dbmb% nt`�l�6�b� 不同波长和厚度的反射率 T.dO0$,Q@$ w%�-!dbmb% nt`�l�6�b� 不同波长和厚度的反射率 T.dO0$,Q@$
3n)iT�SU�3
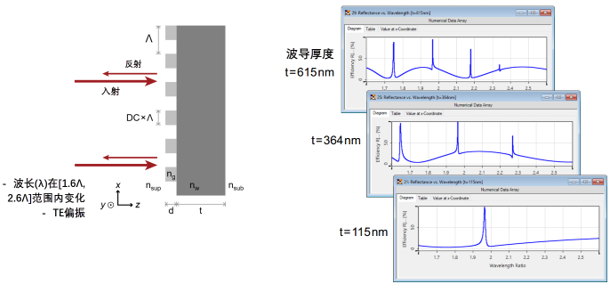
 |M��rH@v7S @Iat�lz*�W 不同波长和厚度的反射率 3V�B�V_/i; |M��rH@v7S @Iat�lz*�W 不同波长和厚度的反射率 3V�B�V_/i;
�b!P�;xLcb 仿真结果来自参考文献: R~(.uV�`#j G. Quaranta, G. Basset, O. J. F. Martin, and B. Gallinet, Laser & Photonics Reviews 2018, 12, 1800017. [Fig. 3 a) H�O�N[{Oq
SLB� iQd.
VirtualLab Fusion的仿真结果 Vta;ibdeqW
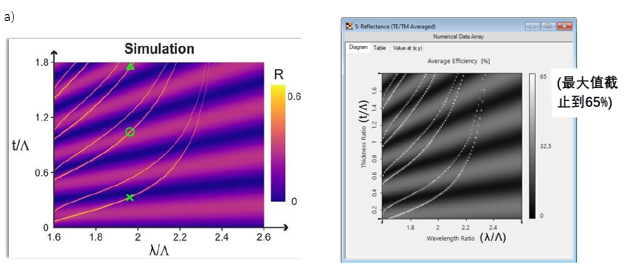 s�'=]a-l~� 特定波导厚度的反射率 �XdVC�>6� s�'=]a-l~� 特定波导厚度的反射率 �XdVC�>6�
r�z7b�%�WY
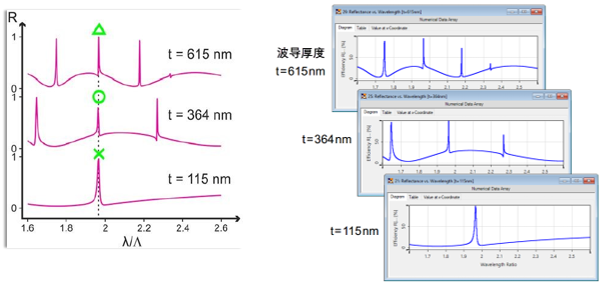
 r+�Cha%&D� 3A1kH` X^q 特定波导厚度的反射率 e(5R8�u��d r+�Cha%&D� 3A1kH` X^q 特定波导厚度的反射率 e(5R8�u��d
o�h~Db�u=% 仿真结果来自参考文献:
6)j4
�TH� G. Quaranta, G. Basset, O. J. F. Martin, and B. Gallinet, Laser & Photonics Reviews 2018, 12, 1800017. [Fig. 3 c) ��u�C�r��� bFXCaD!�{G
VirtualLab Fusion的仿真结果 Di=6.gm�[<
TrA��Uu`?#
 O��m{ML,d
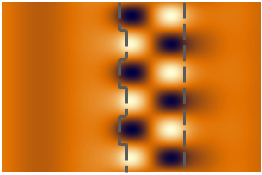
谐振模式可视化(@λ = 687 nm) !]�T�|=y�w .lS6�K�Bf@ O��m{ML,d
谐振模式可视化(@λ = 687 nm) !]�T�|=y�w .lS6�K�Bf@ 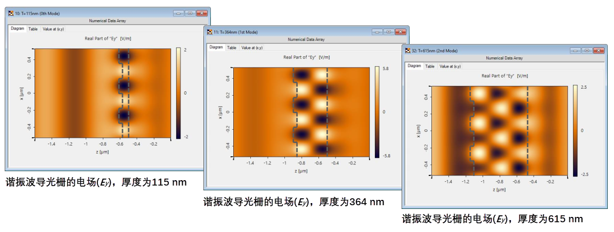 `<Nc��
Y* `<Nc��
Y*
@"2-tn@q_� 角灵敏度分析(t = 364 nm @λ = 632.8 nm) t!N�>0]:mo 1'B�?f#� s  B�
~�Gy�S" '|r�!yA�O6 用聚焦高斯光束检验共振效应 �\MPy"u��C [_Z3v�,vt, B�
~�Gy�S" '|r�!yA�O6 用聚焦高斯光束检验共振效应 �\MPy"u��C [_Z3v�,vt, 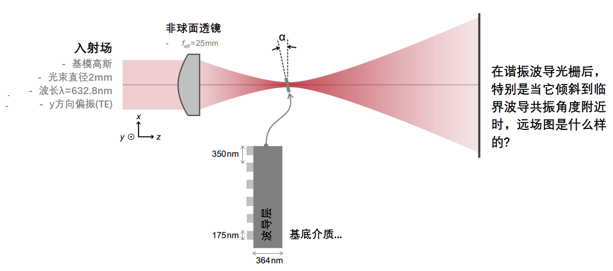 qm_��E/�B� qm_��E/�B�
(<-0UR]%q; 用聚焦高斯光束检验共振效应 �% m$�Mn�x _<�Tz�1>j= 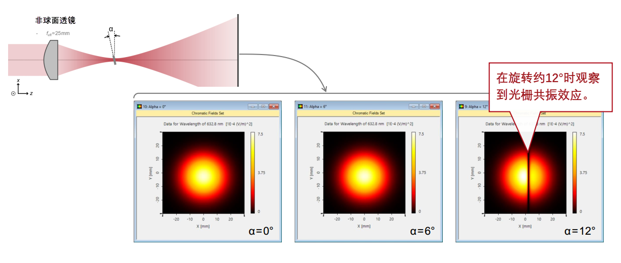 mL+�ps x�+ mL+�ps x�+
3Mt���6iZW 用聚焦高斯光束检验共振效应 }]�@�
"t)" ��-f��n~y1 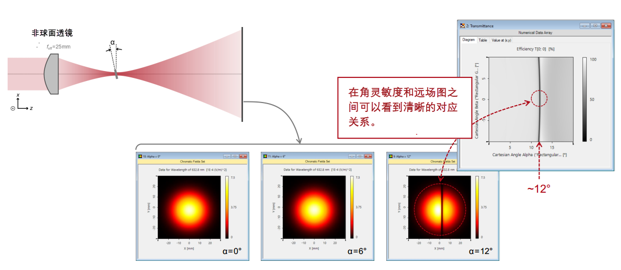 �$�5O&[/�L ?-i&6�i6�Y 走进VirtualLab Fusion �7�.-|3Wcg �$�5O&[/�L ?-i&6�i6�Y 走进VirtualLab Fusion �7�.-|3Wcg
�7T�78S�&g
 ���c5��u?\ r]�{�:�{�Z VirtualLab Fusion的工作流程 �;pq�4El_� ���c5��u?\ r]�{�:�{�Z VirtualLab Fusion的工作流程 �;pq�4El_�
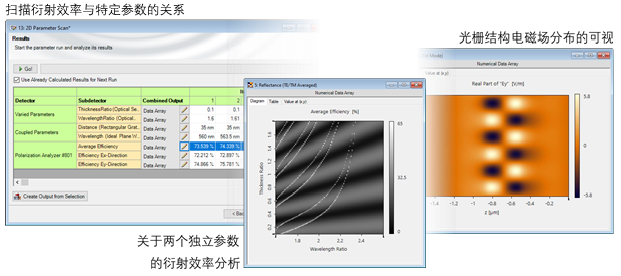
8a1{x(\�z. 构建光栅结构 [c~zO+x��� - 利用界面构建光栅结构 [用例] �3�5et�+9� - 利用特殊介质构建光栅结构 [用例] 9m>_q�Wa�A E2c�m�T�$6 分析光栅衍射效率 y�mu�#�u�� - 光栅级次分析器 [用例] >ZWm�0nTr� p�s�[�rYy� 通过参数运行检查不同参数的影响 �3�f
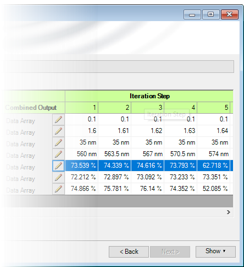
x�!\ - 参数运行文件的使用 [用例] �5@\<:Z�mi Zg�tO�y|?| 计算光栅结构内的场 M�I��3�_<[
{f�s(+
0ei
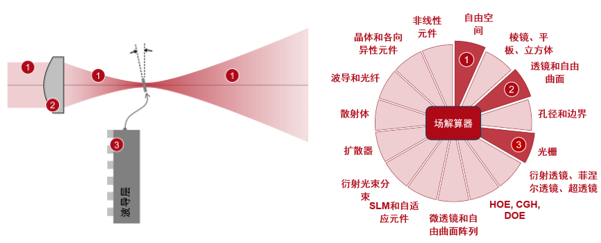
 ��R��lu;l� �0'",4=c#V VirtualLab Fusion技术 Pc-H�QU��� Q}]u�n]]Zt ��R��lu;l� �0'",4=c#V VirtualLab Fusion技术 Pc-H�QU��� Q}]u�n]]Zt
 i[swOY�z]X i[swOY�z]X
|