-
UID:317649
-
- 注册时间2020-06-19
- 最后登录2026-03-05
- 在线时间1939小时
-
-
访问TA的空间加好友用道具

|
�1#�4P�G'H
文章来源:Bäuerle A, Bruneton A, Wester R, et al. Algorithm for irradiance tailoring using multiple freeform optical surfaces[J]. Optics express, 2012, 20(13): 14477-14485. w�gRs���Z�
�T!�}[�yW
主要内容:本文基于最优化质量传递(optimal mass transport)多自由曲面光学的设计算法,结合照明设计软件FRED模拟了洗墙灯实例。使用该算法,可直接调整多面光学系统(在本文中,我们用了双边自由曲面)获得了近似于预先确定照度分布,而同时可捕获从光源发出的大部分光线。增加多曲面自由度可用来减小菲涅尔损失,包含加工上的约束以及减小零件尺寸。 2���',w[I
Axel Bauerle, 1, 2 Adrien Bruneton, 1∗ Rolf Wester, 2 �?k�z�+R�' Jochen Stollenwerk, 1, 2 and Peter Loosen1, 2 yj(v�kifEB 1Chair for the Technology of Optical Systems, RWTH Aachen University, 52056 Aachen, wB{�;b�B�{ Germany 1uk�0d`JL� 2Fraunhofer Institute for Laser Technology ILT, Steinbachstr. 15, 52074 Aachen, Germany a`u
�S[r�> rUjdq/I:Z� 摘要 ~b|`��'k�U
E|$O�h�a[ 自由曲面透镜和反射镜的设计能够获得非径向对称的照度分布,且同时保持光学系统的紧凑性。对于点状光源来说,比如LED,为了增加发光效率往往需要捕获一个宽角度的光源。这样往往导致的结果是产生强弯曲光学元件,需要两个透镜面作用于总的光的折射,从而最小化菲涅尔损失。在本篇文章中,我们报道了一个基于最优化质量传递(optimal mass transport)多自由曲面光学的设计算法,并结合光学工程仿真软件FRED对一般照明问题给出了应用实例。 FHPXu�59�u
^�Mk%z9
�? 1.前言 J!*/a'C�v�
��=6�0~�UM 在照明应用中,透镜和反射镜可以以一种预先确定的方式上分配光线,市场上对这种透镜及反射镜的需求越来越多。为了获得常用的光分布,光学设计中自由度数量必须高于传统的光学元件,这就引入了自由曲面光学的概念,对此有众多设计算法提出[1-5]。折射式光学元件(透镜)在材料-空气界面会遇到菲涅尔反射,控制其精准的路径来避免损失难度较大。因为随着光线角度倾斜菲涅尔反射在增加,因此理想情况是使用几个自由曲面来增加系统的光学效率,在这种情况下,一个单透镜面足以调整照度分布。 ')$NfarQ�.
U70]!EaT�� 到目前为止文献中发布的设计算法,只有Minano、Benıtez[5]提出的SMS3D方法可以直接裁剪多平滑表面,且同时获得预定的照度分布,甚至在一定程度上可把扩展光源考虑进去。然而,据作者所知,SMS3D算法只是在他们团队内部使用。对于点光源的情况,Ries 和Muschaweck[2]得出了一组偏微分方程来描述单个光学面,但一般对于多光学表面目前还没有报道。 m�G�1�IQ�!
sW^a`��V�M 在本文中,基于传输理论的公式[6],对两个自由曲面和一个点光源发射器的照度调整问题,我们提出了灵活的近似解算法。此外,我们利用FRED软件演示了对于一般照明设计任务的可行性。 �KYx�B�VgJ
�>�u(>aV|A 2.光线映射:有关光学设计的传输理论 �eb8w�~���
a%Jx
`��hx 在一般的公式中,质量传输理论讲述了最优路径的计算,此计算允许从初始质量分布到目标质量分布的连续传递。就光学而言,光通量扮演了重要的角色,投射光源描述为在2维空间 上光通量密度 (图1)。类似的,目标空间 上的光通量密度为 。为了清楚起见,在3维空间中,假定 平行于2维平面,光通量密度 和 在各自的局部笛卡尔坐标(x,y)下被参数化(图1)。 M-uMZ�Q�e 图1.映射计算图,点光源投射到平面 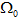 及目标照度投射到 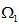 ,自由曲面位置在 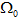 和 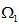 之间。 光学系统(自由曲面)的设计任务相当于发现一个微分同胚映射(光线映射),以便于照度分布转换匹配目标分布: �W�WZ9�._� 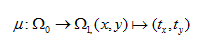 (1) 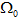 上的(x,y)在 上的(x,y)在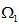 上的目标点。因为沿着无穷小灯管从光源到探测目标上光通量守恒,照度转换公式可以写为: c�ub�k]~VD 上的目标点。因为沿着无穷小灯管从光源到探测目标上光通量守恒,照度转换公式可以写为: c�ub�k]~VD 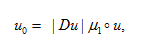 (2) 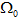 上积分此公式得到了总的能量守恒关系 上积分此公式得到了总的能量守恒关系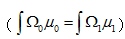 。 n�B ".�'�= 。 n�B ".�'�=
�7�.+�#zyF 因为映射u并不是独一无二的[7],在光学设计任务中主要的限制是发现可引导光学表面连续可微的映射。这也就是所谓的表面法向矢量N可积条件[8] =4�� X]g�W
�����T��^} N*curl(N)=0 (3) /+3��a n9h
计算强制满足方程(3)的光线映射并不是简单的事情,因为由雅克比判决式(Monge-Ampere-type 方程)可知方程(2)一般等效于非线性二阶偏微分方程。处理两个光学表面而不是一个光学表面使这个问题更具挑战性。 �._9�6*r=o
<v�bIp���& 3.近似最优化光线映射 ��6dEyv�99
U^Tp6�vN d 表面法线矢量场直接关系到映射信息(通过斯涅耳折射定律)。因此,即使现在还没有被证实,看起来似乎是可信的:如果光线映射的旋度自身减小,表面法线矢量场的旋度可大幅度减小。 ^�5����t�
{�hO`6mr&t 使用最新的质量传递理论有助于实现这一目标。在处理预定的目标函数这方面大部分的工作集中在寻找最佳映射。每个元件的位移、质量权重是具有代表性的二次函数。几种不同的解决问题的方法已经被提出[9]。本文中,我们关注于在图像变换的背景下由Haker提出的一阶、无参数方案[7]。 VI��R�.�yh
e|r0zw� �S 点光源的光通量分布投射到方形的2维空间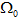 ,因此获得了平坦的光通量密度μ。一个改进的立体投影通常用于获得这个通量密度,与此同时控制可捕获光锥角度。同样的目标上的光通量分布投射到一个平行的方形区域 ,因此获得了平坦的光通量密度μ。一个改进的立体投影通常用于获得这个通量密度,与此同时控制可捕获光锥角度。同样的目标上的光通量分布投射到一个平行的方形区域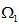 。如图1所示。 VR���W]��a 。如图1所示。 VR���W]��a
�:Ld!mRZF Haker的步骤[7]是首先找到μ0和μ1初始映射关系(通常是在笛卡尔坐标轴上两个连续1维数值积分),初始映射结果用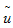 表示。 ,A5)����<} 表示。 ,A5)����<}
<3��9!G7ny Haker演示了μ0和μ1所有映射可用连续变量t表示,同样的,u可以看作t的函数,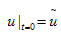 。通量符合如下演化方程: s/1 ��#DM" 。通量符合如下演化方程: s/1 ��#DM" 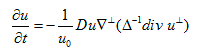 (4) 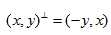 代表在二维空间旋转90度, 代表在二维空间旋转90度,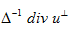 是f的解,表示为泊松公式 是f的解,表示为泊松公式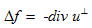 。 u.|~$yP.�! 。 u.|~$yP.�!
qOG}[%<^n7 这个方程的稳态解(当t--->∞ )已经被Haker证明了是二次型性能指标最优化映射。本文中,此方程的解使用Hakert数值技术,使用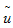 作为初始点。注意演化方程本身不使用μ1作为相关信息,因为它已经包含在初始映射 作为初始点。注意演化方程本身不使用μ1作为相关信息,因为它已经包含在初始映射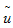 里面了。 gK3Mms�]}m 里面了。 gK3Mms�]}m
�"�MiD8wX- 用这种方法减小映射的旋度会得到一个好的积分近似条件,如下面第五部分所示。 :<~7y.*O{�
*xM�/��;)� 4.由光线映射构建光学表面 8"vwU�@cfC
q�sg>5�E�� 使用映射信息,光学表面的计算可促使光源光线偏转到想要的目标位置。总的光的偏转分成几个部分(在如下的例子中描述了两种),对于一个给定的光学面,每个都可实现。在本文中,构建方法是使用标准的最小二乘优化法。表面使用三角形网格画法顶点为i=1,……N,他们的位置为由下列式子给出: �)-/gL�Zsx 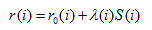 (5) 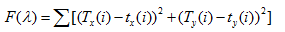 (6)
!|m�9����| 表面构建是基于目标面上的光线坐标符合积分条件。算法与在目标面上的光线位置协调进行,因此可在多个光学表面偏转光线,引入额外的自由度到设计上而并非算法上,因为算法只考虑单个面。 � 9|S`�ub'
YJ2r��o-X� 使用三角网格算法的优势体现在可非常灵活的进一步处理结果表面。例如他们可以细化处理或快速切割,因此,引入了出色的透镜边界控制条件。结合多面设计允许包含加工限制条件(如注塑成型可避免凹陷)。 ���pyW� u9 �xUYo��w�
5.建筑照明:洗墙灯实例应用 lz~J�"$��b
��cQ�FR]i� 图2给出了标准的、高光学效率,建筑照明上具有挑战性几何结构,吸顶灯距离均匀照度接受面80cm。第一步,建立一个简单的轴上演示设计,并对比了传统的非-优化的映射(1维逐次积分)设计。基于此,建立了更具有挑战性的倾斜设计。 ZcryA�m:�I 图2.(a)自定义坐标轴的洗墙灯应用 (b)简单的轴上方案 M}�.b"
ljZ
5.1 轴上实例 rvwy~hO"
s�!6=|S�S7 依据上面列出的算法,一个初始的光线映射计算出来,并构建了相应的光学表面结构(假设材料是PMMA,n=1.49),最小化目标函数(公式6)。为完善设计,对如上的初始映射进行了优化,第二组表面随后被构建。图3给出了相应的映射,分别表示为规则网格的变形及z分量的旋度。当系数为200时总的旋度量急剧减小。 ui�B�TnG�" 图3. 光线映射(表示为规则网格的变形)及相应的Z分量旋度映射,(a) 优化前 (b) 优化后 8kW�/D�cLE 在两种表面处执行了蒙特卡洛光线追迹,图4给出了每种情况的最终照度分布。500万条光线、目标面上探测器分辨率点为71*71,所有的这些均由FRED[10]光学工程仿真软件来完成。光源是标准的朗伯体点发射器,半角分布为70度圆锥角,方向沿着z轴。 CM~MoV[k7e 尽管透镜的形状极其相似,图4(d)中的光分布显示了与均匀照度分布相比显示了极小的变形。证实了旋度减少得到了令人满意的光线映射,例如与初始映射相比更好的与积分条件(公式3)的匹配,同时更接近想要的光通量变化。 "6�I[4U"@� s=E���i��H hE!7R�M+Y 图.4 FRED软件线框图示及用蒙特卡罗光线追迹后辐照度分布(任意单位)。(a)和(c)没有映射优化;(b)和(d)映射优化后 �?(�i�m�+2
5.2 轴外结构 +CTmcby�Oi
F1A1@{8�bN
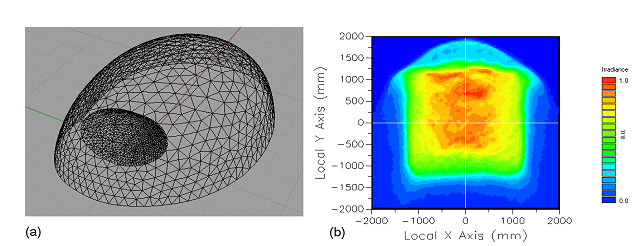
图5显示了光线映射优化后洗墙灯透镜表面3维CAD模型与预计的照度分布。考虑到如光轴与目标面高的倾斜角度、光源到目标面短的距离及目标面上均匀照度分布(2.8*2.8m2)等有难度的配置,我们选择在方形区域中心2m*2m处,y轴横截面强度变化小于10%,x轴横截面强度变化小于30%。X和y强度值的不对称源于光学元件相对于目标面的倾斜。最后,蒙特卡罗模拟显示超过78%的光源光功率转移到了目标面上,包含菲涅尔损失,因此,说明了本透镜设计具有非常高的光学效率。因为光源锥角太宽导致菲涅尔损失较大(总的光学效率减少到70%),未能达到想要的目标照度分布。 >v0��:qN7|
 (buw^
,NwZ (buw^
,NwZ
图5.(a)自由光学曲面线框图 (b)洗墙灯蒙特卡洛光线追迹后照度分布 �;�WI]�vn�
mPmB6q%)�]
6.比较一个自由曲面和两个自由曲面的菲涅尔损失 �+*t|yKO>[
e!o(g�&wBj
 $+:�(f{Va* $+:�(f{Va*
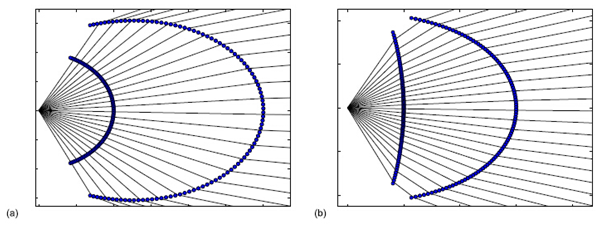
图.6 二维光学系统的曲线图 (a)1个被激活自由曲面偏转光线 (b)2个被激活的自由曲面可减少菲涅尔损失 M�<�qu�di�
U7%28�#@��
为了评估透镜的菲涅尔反射损失,我们已经知道了光源光线到目标点的映射,同时也知道了其几何形状。建立单个被激活的自由曲面,第一个透镜面选为半球面,其中心点在点光源位置上,如图6所示,第一面没有提供任何的光线偏转,第二面必须执行整个光线映射。相反的,如果使用2个自由曲面,光线沿着第一个面偏转,如图6中所示。 d]M[C[TOX�
F�WTx&Ip�
为了分析菲涅尔反射,光线原本想透射出表面但被反射回去的光线均认为是菲涅尔损失。 M@^U�0
?��
�LC'2q�*:'
对于离轴洗墙灯的情况(如图6b所示),在两个面的偏转角度平均分配前提下计算表面面型。菲涅尔损失是光线总的反射损失,可由菲涅尔公式给出[11]。图7分别计算了使用1个自由曲面及两个自由曲面的菲涅尔反射。 d~�[U�XQ�C
$ly0�h� W
 :���z�~!p~ :���z�~!p~
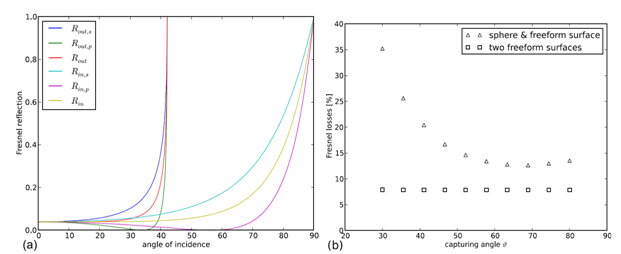
图.7 (a)菲涅耳反射是入射角在光学表面的函数(Rin是光线进入透镜的反射率,Rout是光线离开透镜的反射率;S是垂直偏振光,P是平行偏振光,没有添加偏振态的平均值);(b)是两个有效透镜表面与单个有效表面系统的菲涅尔损失随捕获角度的变化。 �g�EKO128
���6D9o08�
透镜的总菲涅尔损失也取决于光源可捕获的角度,高的光学效率需要高的捕获角。随捕获角度的变化两面系统菲涅尔损失几乎是常量。这是由于两自由曲面系统中每一个面的入射角度没有超过特定的临界值,超过此值菲涅尔反射显著增大(图 7(b))。在目前例子下,最大入射角度典型的低于30度,这与单个自由曲面的例子形成了强烈的对比,它在第二个透镜面最大的入射角非常接近于全反射,因此显示了非常高的菲涅尔损失。 ~Ob�8i�1S>
z
Z�%/�W)t
两有效面总的菲涅尔损失在8%至10%左右,非常接近于正入射的损失,然而单个有效面的最小值在15%左右。由于相当大的扰度作用,单个有效面透镜小的捕获角造成了菲涅尔损失强劲增长,而大扰度是指引光线到目标面的边缘区所必需的。在第5部分计算得到菲涅尔损失与这里估算出来的结果相当吻合。 G6Q4-k�cK�
aW@o�E
~`
7. 结论 �AA7#��c7�
5�V|tXs�y:
我们演示了一个新的两步光学设计算法,直接由提供的初步结果使用多自由曲面调整照度分布。这种算法计算速度快(在当今的台式算机上几分钟即可完成计算),并在一般照明应用上验证了其适用性和实际意义。第一步主要计算从光源光线到目标点的映射,随后最佳化使其无旋度,在第二步中,使用从目标面映射提取光线位置计算光学面。当然,这个模式同样适用于反射元件,本文没有进一步的深入。 HP$�K.a7�H
piu0^�vEEH
使用该算法,有可能直接的调整多面光学系统(在本文中,我们用了双边自由曲面)获得了近似于预先确定照度分布,而同时可捕获从光源发出的大部分光线。增加多曲面自由度可用来减小菲涅尔损失,包含加工上的约束以及减小零件尺寸。
hh&Js'�d�
/`R �dQ<($
参考文献 �R|�t;�p!T
Y�Y!�!�<2_
1. J. S. Schruben, “Formulation of a reflector-design problem for a lighting fixture,” J. Opt. Soc. Am. 62, 1498–1501 (1972). zPQ$�\$7xB
2. H. Ries and J. Muschaweck, “Tailored freeform optical surfaces,” J. Opt. Soc. Am. A 19, 590–595 (2002). kGD�|�c=K}
3. W. A. Parkyn, “Illumination lenses designed by extrinsic differential geometry,” Proc. SPIE 3482, 389–396 (1998). ��!3K�PwI,
4. V. Oliker, “Designing freeform lenses for intensity and phase control of coherent light with help from geometry and mass transport,” Arch. Rational Mech. Anal. 201, 1013–1045 (2011). *o��|p)lH
5. P. Bentez, J. Miano, J. Blen, R. Mohedano, J. Chaves, O. Dross, M. Hernndez, J. Alvarez, andW. Falicoff, “SMS design method in 3D geometry: Examples and applications,” Proc. SPIE 5185 (2004). R��]=SWE}U
6. A. Bruneton, A. B¨auerle, P. Loosen, and R. Wester, “Freeform lens for an efficient wall washer,” Proc. SPIE 8167, 816707 (2011). J<_�1z':W)
7. S. Haker, L. Zhu, A. Tannenbaum, and S. Angenent, “Optimal mass transport for registration and warping,” Int. J. Comput. Vis. 60, 225–240 (2004). b]dx�lj}
<
8. F. R. Fournier, W. J. Cassarly, and J. P. Rolland, “Fast freeform reflector generation using source-target maps,” Opt. Express 18, 5295–5304 (2010). \Ut�S>4w�\
9. L.-C. Evans, “Partial differential equations and Monge-Kantorovich mass transfer,” tech. rep., Department of Mathematics, University of California, Berkeley (2001). �{Tx 3$�eU
10. “FRED Software - Optical Engineering,” http://www.photonengr.com. Y�\u_+CG�*
11. W. Born and E. Wolf, ”Basic properties of the electromagnetic field,” in Principles of Optics 7th ed. (Cambridge University Press, 1999), pp. 41–42 /'�Bdq?!B&
J3\�)�Jy��
`Gk�Rmv*�
注释: Y~GUR&ww0n
FRED Optimum 是一套由Photon Engineering所开发出来的光学工程仿真软件,作为光机一体化的开发平台,可以用在光学设计过程中的每一个环节,包括最初的概念验证,整合光学设计和机械设计,对虚拟原型进行全面分析,对模型参数进行快速公差分析和优化。它的显示窗口为3D实体显示工作平台,具备快速的光线追迹功能,并且可以同时允许32核CPU进行多线程运算。 V~c(]K��)-
功能优势: 7��z>�+�w�
多软件接口,可导入其他光学软件(Zemax、CodeV、OSLO、ASAP)进行整个光机系统性能评价,包含光线路径、MTF、光程差、杂散光路径、鬼像、PST与关键被照面、衍射、冷反射、红外热成像分析。 -wIM�0�YJ�
CAD导入无破损,可以导入CAD 模型并修改其参数和光学性质。 &�z0iLa4q)
整机装配、pick up解、公差与灵敏度分析。 #wD7� \X-f
真实三维模型渲染和实时显示窗口,可以直观快速的找到光机系统中尺寸不匹配常见问题。 7xR|_+%�~K
可分析光学系统的三阶像差、波像差、振幅、相位等光信息。 ={xqN�RVd
具有序列与非序列光线追迹能力,光线追迹数量数没有限制。 A[R�N-�R�,
可多达32核CPU的多线程运算能力。 ct.Bg���)E
拥有内置混合优化功能,拥有fractional weighting功能以链接变量,可进行局部和全局优化,可内建或从CAD导入的NURB表面进行优化,可大大减轻照明等领域的设计中繁重的工作量。 | /#'S�&!U
支持VB脚本编程,包含非常多的命令语言。可支持创建和修改几何模型、光源、镀膜、材料、散射模型以及进行光线追迹和计算分析,实现功能扩展。 ��
/Ef4EX0
14+BSDF散射模型,可用来仿真机械元件的表面散射,每个元件可赋予多个散射模型,所有的这些散射模型混合可形成成千上万的散射模型,并可模拟透镜表面粗糙度。 �D`��fc�7m
拥有多种体散射模型,并支持脚本自定义散射模型,支持荧光粉、光学元件内部缺陷的散射模型等。 �\#_@qHAG�
支持IES TM-27-14 XML光谱文件直接导入。 q��"p#�H�8
FRED可以仿真同调及绕射光学系统,使用相对简单但是有效的光线追迹的扩展方法,一般称为高斯光束分解。任何复杂的光场可以分解为高斯光束,这个方法允许我们可以处理相干光、偏振态,如高斯光源、相干性、光纤耦合分析,使光源更符合实际情况。可与FDTD Solutions 的矢量场数据交换,来处理宏光学系统和微结构光学。 c��qHw^{'8
COM服务器/客户端支持与Matlab Excel 等程序相互调用。 7C���YH'DL
模拟太阳光在不同位置、不同时间以及一系列环境因素如大气气溶胶厚度、大气可降水量、表面压强等对接受面照度影响。 R]V��TV7D�
无级次限制的衍射光栅效率计算。 &}�|0C�R.(
<mn-�=�#)�
S
`wE$s�o>
QQ:2987619807 �}9��FD/��
|