在本文章中,我们将展示色散补偿方案如何影响系统性能。色散的脉冲展宽效应导致相邻位周期中的信号重叠。这称为码间干扰(ISI)。展宽是距离和色散参数D的函数。色散参数以ps/nm/km为单位,随光纤的变化而变化。它也是波长的函数。对于标准单模光纤(SMF),在1.55um波长范围内,D值通常大约为17ps/nm/km。对于色散位移光纤(DSF),在同一窗口中的最大值为3.3ps/nm/km。非零色散光纤(NDF)的色散范围为1~6ps/nm/km或-1~6ps/nm/km。 _4TH�4~�cY ^L0d��/,ik 对于外部调制光源,受色散限制的传输距离为 �r�`%+M7�� og4UhP^UET 当D=16 ps/(km nm)和2.5 Gbps时,L≈ 500km,而在10gbps比特率下,它下降到30km。色散补偿光纤或光纤布拉格光栅等技术可以用来补偿光纤中累积的色散。在下面的例子中,我们将展示三种不同的方案,前补偿、后补偿和对称补偿,以补偿光纤色散。首先我们将使用色散补偿光纤(DCF)。然后我们将展示色散补偿器的累积色散量如何影响性能。在这种情况下,我们将使用一个理想的色散补偿模块(DCM)作为色散补偿器来说明这个想法。 �syk!�7zfK
]F�D�'5�p{ 用DCF进行前、后、对称补偿 H&F9J��^rC
前、后和对称补偿配置如图1、图2和图3所示。在我们的模拟中,我们在每根光纤后面使用了光放大器来补偿跨距损耗。SMF的色散参数为120km长和16ps/nm-km。因此,总累积色散为16×120=1920 ps/nm。这种很大的色散可以通过使用一个24公里长、色散为-80 ps/km nm的DCF来补偿。总传输距离为120×2=每种情况240公里。在补偿后的情况下,DCF放在SMF之后。在对称补偿情况下,光纤的放置顺序为SMF、DCF、DCF、SMF。 ilK-�?�@u+ �cQG
+$0�( 图 1: 色散后补偿
(]�_��1�� 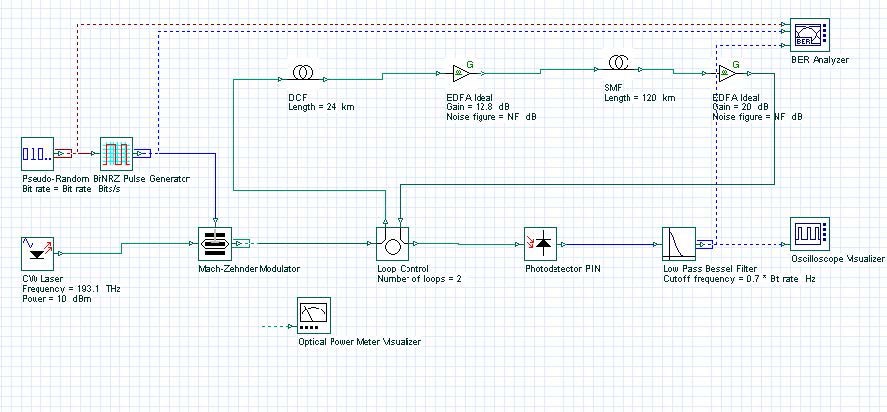
图 2: 色散前补偿
�Tskq)N�U� 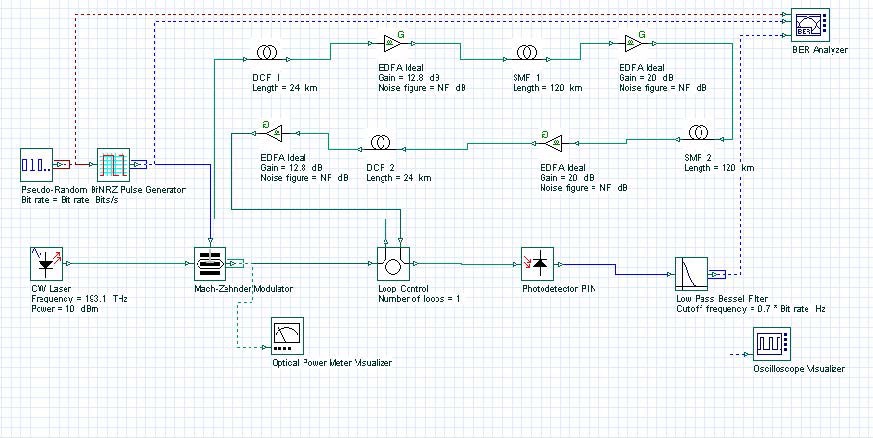
图 3: 色散对称补偿
rxr{/�8%f% 在这些模拟中,我们使用了NRZ调制格式。2.5 Gbps的接收机灵敏度为-28 dBm,10 Gbps的接收机灵敏度为-25 dBm(接口的热噪声为2.048e-23W/Hz。)模拟结果如图4和图5所示。图4显示了这三种方案在2.5 Gbps比特率下接收信号的Q因子与发射信号功率的关系。图5显示了10 Gbps比特率的相同图形。要以10 Gbps模拟设计,需要将全局参数比特率设置为10 Gbps。从这些数字,我们可以得出结论,最佳性能是通过使用对称色散补偿获得的。最坏的情况是色散预补偿。这也可以从图5给出的眼图中看出。这些结果与文献[2][3]中的结果完全一致。 (Lo%9HZ1Mx ~i@�Y|3�8C 图4:Q因子与2.5和10 Gbps比特率下的信号功率之比,用于前、后和对称色散补偿 qe��#P�?�[
图5:前、后和对称色散补偿在2.5和10 Gbps比特率下的系统性能。眼图所示为-12和10 dBm信号功率。 |\_^��B���
1<+2��kBuY 利用DCM实现色散补偿
�A"`foI$0� 我们现在将展示补偿色散量如何影响系统性能。我们将使用一个理想的色散补偿光纤光栅作为色散补偿模块(见图6)。在这种情况下,我们选择了后补偿方案,因为它比对称补偿方案简单。 �&P.4�(1sC
"dsU>���3u +�${D����� 图 6: 利用DCM实现色散补偿
��D*Ik7�Pe SMF的总累积色散为16×120=1920 ps/nm。我们将FBG的总色散范围从-30扫到-3000ps/nm。比特率设置为10 Gbps。在这个模拟中,我们要研究系统的色散限制性能。为了避免触发光纤非线性,我们将接收功率保持在-3dbm。其他例子将考虑残余色散对非线性效应的影响。图7显示了Q因子与剩余色散的关系。模拟结果表明,在线性区(低功率),完全补偿光纤色散效果最好。过度补偿会降低系统性能。 fKp#\tCc y MWI4Y@1b�S 图 7:Q因子与剩余色散 �A�v�?2<��
References: R�E�}?5XHb [1]G. P. Agrawal, Fiber Optic Communication Systems, Wiley-Interscience, 1997. ,�\�X@�~�j [2]R. Ramaswami and K. N. Sivarajan, Optical Networks: A practical Perspective, Morgan Kaufmann, 1998. �ub7z��A!% [3]M. I. Hayee and A. E. Willner, “Pre- and post-compensation of dispersion and nonlinearities in 10-Gb/s WDM systems”, IEEE Photon. Tech. Lett. 9, pp. 1271, 1997. DK�fE.p)�� *"WD�b|PBb
cKN$� =gd� QQ:2987619807 �;GVV~�.7/