光束传输系统(BDS.0005 v1.0) fa�VS2T�N4
���b\L)m (
二极管激光光束使用无色散离轴反射装置进行准直和整形 MVA��c8d�S
�&7F&}7*c�
�Mf7�E72{D �>4'21�,q�
简述案例 -A���@U0=o I"V3+2��e� 系统详情 �)dg U�mN� 光源 �'�#f��?#( - 强象散VIS激光二极管 Z�OHRU��m 元件 ��6DZ2pT: - 光束准直和整形的反射元件(例如圆柱抛物面镜) 6QptK�Xu�7 - 具有高斯振幅调制的光阑 m){�&:H�s� 探测器 Ph\F'xR�Oe - 光线可视化(3D显示) m��t��.,4� - 波前差探测 N[{]�i���Q - 场分布和相位计算 ~�[;�{� � - 光束参数(M2值,发散角) 2�o}8W�7y� 模拟/设计 )�fR1n}#�� - 光线追迹(Ray Tracing:):基本系统预览和波前差计算 gD40�y\9r� - 几何场追迹+和经典场追迹(Geometric Field Tracing Plus (GFT+) & Classic Field Tracing): nK�:`e9E�S 分析和优化整形光束质量 EQ~I'#m7�� 元件方向的蒙特卡洛公差分析 d.�1Q�~�&` Q�2R>l�zB� 系统说明 V,'��F�l�U B)�d�@RAk� 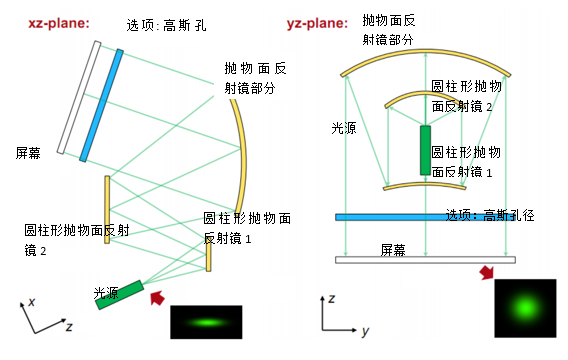 ZArf��;&�8 模拟和设计结果 �GD/�nR4�$ :O#gJob-%s
ZArf��;&�8 模拟和设计结果 �GD/�nR4�$ :O#gJob-%s 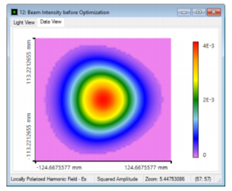
 �P#�9-bYNU
�P#�9-bYNU 场(强度)分布 优化后
r��N'k4V"K
 �gU*I�;�s>
�gU*I�;�s>
 �zN/Gy���} &:��,fb]p� 总结 �,XP�@ �pi
�zN/Gy���} &:��,fb]p� 总结 �,XP�@ �pi
W�.sD2���f 实现和分析高性能离轴和无色散反射光束整形装置。 9�&�[\*�{� 1.模拟 @@�xF#�3 � 使用光线追迹验证反射光束整形装置。 $q=�h�c��u 2.评估 @)� ]t�8�( 应用几何场追迹+(GFT +)引擎来计算场分布和评价光束参数。 ���*x�h�o� 3.优化 �
pe|\'<>i 利用一个具有高斯形状孔径函数的光阑和经典场追迹引擎来优化M2参数。 CTh�1;U20� 4.分析 n/���:Z�{� 通过应用蒙特卡罗公差来分析方向偏差的影响。 �}8X:�?S
% �u��of0Oc. 对于复杂的光束整形装置,特别是离轴系统,可以使用VirtualLab来进行高效的模拟和分析。模拟过程中,根据情况应用不同的模拟引擎。 JC�BnFr�P� 9Z}S�]-u/ 详述案例 r]Z.`}K�km
]dQZ�8yVK� 系统参数 RH1U_gp4 ] �@V*a�u�: 案例的内容和目标 sV;qp�D�XX
!�vi4*
@: 在BDS.0001,BDS.0002,BDS.0003和BDS.0004案例中,研究了折射光束传输系统。 ~�M�D><w�> ;��2 \<M�6  iNMLYY�q]l
iNMLYY�q]l
J#_\+G i�� 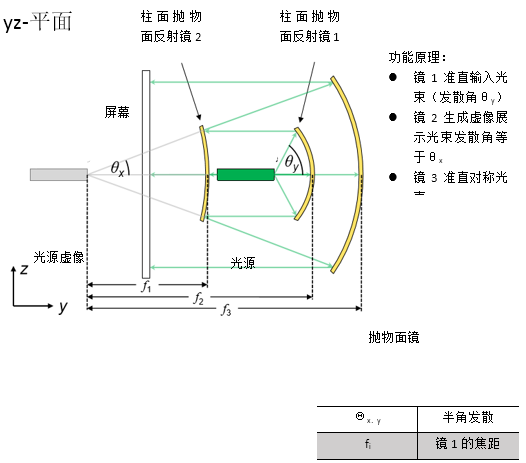 bK6, sa�N> LH�1BZ(5�g
bK6, sa�N> LH�1BZ(5�g 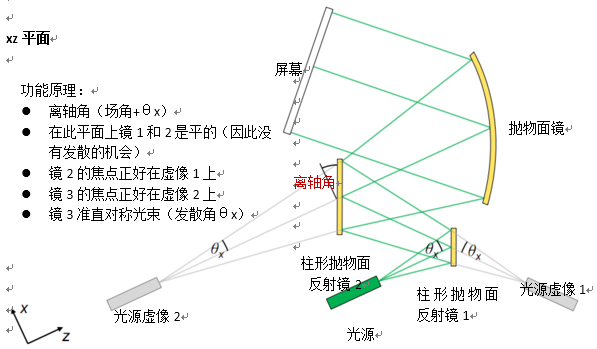 3�" 8�t)s�
}qTv&Z�3$ 规格:像散激光光束 y�RSy(/L^+ (p}�9^��Y 由激光二极管发出的强像散高斯光束 �(g�v=P>�: 忽略发射区域在x和y方向可能发生的移动 7�UY('Q[�
3�" 8�t)s�
}qTv&Z�3$ 规格:像散激光光束 y�RSy(/L^+ (p}�9^��Y 由激光二极管发出的强像散高斯光束 �(g�v=P>�: 忽略发射区域在x和y方向可能发生的移动 7�UY('Q[�
@�faF`8LwA  �nau�~i1��
�nau�~i1��
�&�*h`�b{]
 Z�{j!s6Y@{ 7 B4w.P,�B
Z�{j!s6Y@{ 7 B4w.P,�B
规格:柱形抛物面反射镜 Sf#\�6X<B ��0f�EZD$� 有抛物面曲率的圆柱镜 X:iG[iU*�� 应用用锥形常数.-1来实现锥形界面 )@?��Qt2�� 曲率半径等于焦距的两倍 ajg�7xF{l) BIwgl@t!�> jKe$�&.�q@ 规格:离轴抛物面圆柱镜(楔型) m(Pz7U��.Q q>�wa#1X)� 对称抛物面镜区域用于光束的准直 Opb�szSl"y 从VirtualLab元件目录使用离轴抛物面镜(楔型) <<����~lV5 离轴角决定了截切区域 HQ��jxJd5P _%C_uBLi�� 规格:参数概述(12° x 46°光束) 6T5�A31 �Q +��s�V#�Z, 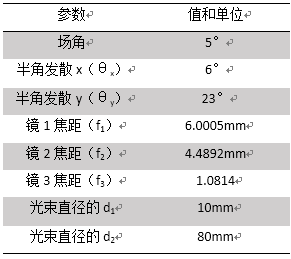
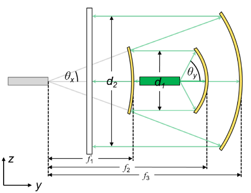 Lcm~QF7cd E�0Wrp��GZ 光束整形装置的光路图 C"V?y�Dy2~ n:{��-Vv�t
Lcm~QF7cd E�0Wrp��GZ 光束整形装置的光路图 C"V?y�Dy2~ n:{��-Vv�t 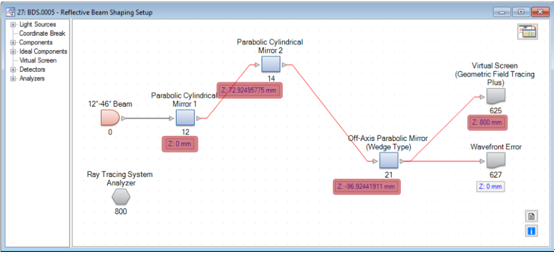 |~1rKzZwF
|~1rKzZwF
F5om-tzy��
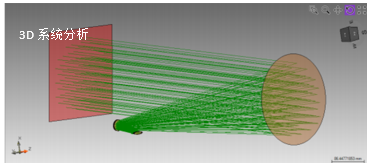
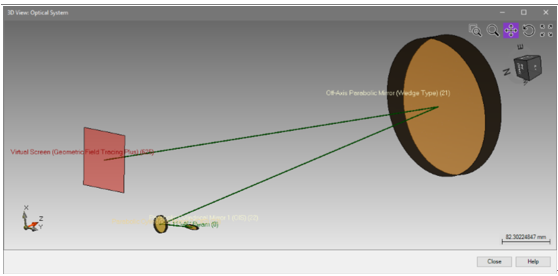 t/E��MBfLc �.F=<�r-0� 光学元件的定位可以通过使用3D系统视图来显示。 4O�B~�h]Vc 绿线表示生成的光轴,由VirtualLab的基础定位方法生成(仅仅设置了距离z和倾角)。 '2i)#~YO< !kjr>��:)x 详述案例 oqQ�?�2k<@ �'�=@H2T6= 模拟和结果 >8.��v.;�` UGez�o3�}� 结果:3D系统光线扫描分析 '�Iq��K �M 首先,应用光线追迹研究光通过光学系统。 '�/n%}=a=� 使用光线追迹系统分析仪进行分析。 9|?�(G�G�� �2�*�3B~"� file used: BDS.0005_Reflective_BeamShaper_01_RT.lpd �hc3��1+TL 519�:yt��� 使用参数耦合来设置系统 `eA&C4oFOO
t/E��MBfLc �.F=<�r-0� 光学元件的定位可以通过使用3D系统视图来显示。 4O�B~�h]Vc 绿线表示生成的光轴,由VirtualLab的基础定位方法生成(仅仅设置了距离z和倾角)。 '2i)#~YO< !kjr>��:)x 详述案例 oqQ�?�2k<@ �'�=@H2T6= 模拟和结果 >8.��v.;�` UGez�o3�}� 结果:3D系统光线扫描分析 '�Iq��K �M 首先,应用光线追迹研究光通过光学系统。 '�/n%}=a=� 使用光线追迹系统分析仪进行分析。 9|?�(G�G�� �2�*�3B~"� file used: BDS.0005_Reflective_BeamShaper_01_RT.lpd �hc3��1+TL 519�:yt��� 使用参数耦合来设置系统 `eA&C4oFOO
0Y�TtA]|`4
���;^�*+:e
自由参数: Ra�1���5d^
反射镜1后y方向的光束半径 �^�`B##9g~
反射镜2后的光束半径 MSrY*)n!>O
视场角,这决定了离轴取向(这些值保存为全局变量) yScov)dp�(
由于功能原理,所有系统参数(距离,焦距,直径)可以由光束参数分析计算。 O�L6x�MToP
对于此计算,应用了嵌入的参数耦合功能。 (tz_D7�c$F
)��b:~kuHi 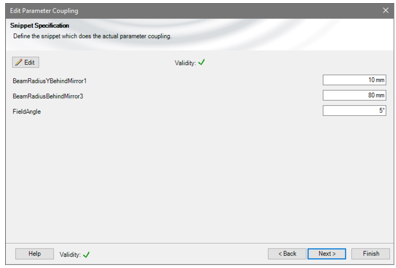 �3
MI�) �E
�3
MI�) �E
k(v���Ep�]
]R3pBC"�Jv
 2 ���|k�H%
2 ���|k�H%
�_|5�F��rN 自由参数: y9l.i��@-
反射镜1后y方向的光束半径 M��}K�M]�< 反射镜2后的光束半径 ws�hp{ ��y 视场角,这决定了离轴取向(这些值保存为全局变量) Rs(�C�rB/M 基于光束发散角和直径(x和y方向)焦点,可以计算并设置反射镜的直径和距离z。 <�PuB3PEvV �1RUbY>K#U �Eg-�M�m4o 如果这个例子评估20个参数,那么返回到光路图(LPD)。
^:��rNoo� .]sIoB-5�4 PU�/�Br;2A 结果:使用GFT+进行光束整形 ��lXL7q?,9 �u�J!s%s2g 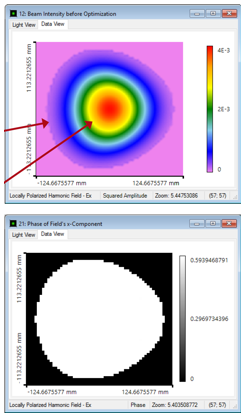 �ba)Yb��P[ �g� � cK" ?U9d3] �W�
�ba)Yb��P[ �g� � cK" ?U9d3] �W� 现在,利用几何场追迹+计算生成的光束剖面。
ff5
Lwf{{� g,G�baaXH� 7�)6Yfa]I% 由于离轴设置,光线分布显示出轻微的不对称形状。
�O]r�3�?=� RN��rYT|�� 不过,场分布几乎是对称的(最好是使用伪色(false colors))。
E(��4lu�%� Z!��=Pc$?� 产生的相位是完全平坦的,产生的波前误差:
;�����h(;( \e�Sk�7�C  8UY=}R2C�� :,z3�:P�L�
8UY=}R2C�� :,z3�:P�L� file used: BDS.0005_Reflective_BeamShaper_01_RT.lpd
TWR#M�VM�I �"VVR#H}{� 结果:评估光束参数 "6o}qeB l� 8iH;GFNJ7' [#*?uu+
jK 从生成的整形光束场分布,可以评估光束参数。 可以直接通过使用探测器界面实现。
p�N��f��9� 在这个例子中,我们对光束半径,发散角和M2值感兴趣。
�,�5+X%~' 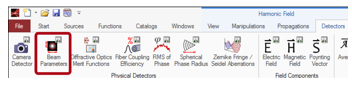 �x_�iy;\s1 �m+8b2�H:V
�x_�iy;\s1 �m+8b2�H:V 整形光束在x和y方向上显示了一个几乎相同的半径。 发散角大约是4urad。
s2v#�evI`+ M2值明显高于1。(与理想高斯光束相比,高M2值是由光束偏离引起的)
 �2Q'��X�B� { �)�GE�gC
�2Q'��X�B� { �)�GE�gC file used: BDS.0005_Reflective_BeamShaper_02_BeamShaping.lpd
Y�1il�H-8� �$��^��D(% 光束质量优化 Ht�X�BaIl\ �/zP)2q�^� /E �
yg*#� 通常,使用合适的高斯调制光阑以用于优化M2值。 因此,我们使用测量的半径作为腰束半径(消除发散角)来生成一个高斯光束。
�YU0HyS�P: 之后,将接收场转换成一个透射函数。 将该传输函数用作光阑(在一个透射函数元件中)。
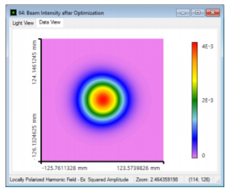
;�gu�>�;�_ }GNH)-AG)$ 结果:光束质量优化 j��l0E��g W�y��JfF=< Nb�9V/2c;V 由于通过高斯孔径传播,光束显示出理想高斯形状。 因此,M2值在两个方向上几乎都是1。
o�/�[y�A3^ F�h4w0u*Q� 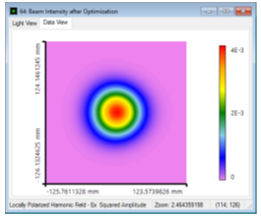 Pd��N\0B�` �_wJ#jJz2�
Pd��N\0B�` �_wJ#jJz2� 然而,光束半径是略有减少。(光束半径显示在最后一张幻灯片是由于其偏离了理想高斯。)
p�z6�-
hi7 TKBK3�N 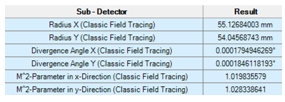 �pmD-]�0��
�pmD-]�0�� file: BDS.0005_Reflective_BeamShaper_03_BeamOptimization.lpd
�LOG*K;v�3 oYm{I� ~" 反射镜方向的蒙特卡洛公差 a1�sLR�qo8 E9*?G4�P{l 对于公差,在随机模式下我们使用参数运行特性。
#V�,~�d&_k �/�ZN5�WK� j#>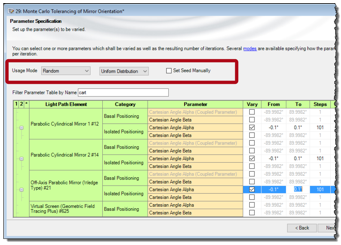 x��4A~MuGU .�/�*,Thc ;�Kb[UZ��1
x��4A~MuGU .�/�*,Thc ;�Kb[UZ��1 对于这个例子,假设每个反射镜都有±0.1°的角度偏差(绝对的方向)。 由于这个偏差,整形光束的波前差明显增加。
k�<";t���� 这意味着,波前对对齐误差很敏感。
�tsC|R~wW� �_$_�C�R\$ 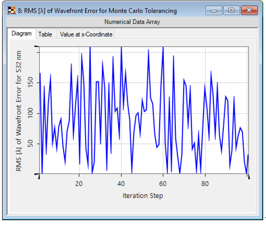 �y\|\�9Q%D �im[�g�bac
�y\|\�9Q%D �im[�g�bac file used: BDS.0005_Reflective_BeamShaper_04_Tolerancing.run
5�*z�a] � �V�R�P.t�D 第一个随机公差的典型强度分布:(相应的均方根波前差:1.08λ,40.4λ,140λ)
Wq�&���c,H !�4cd�P2^P 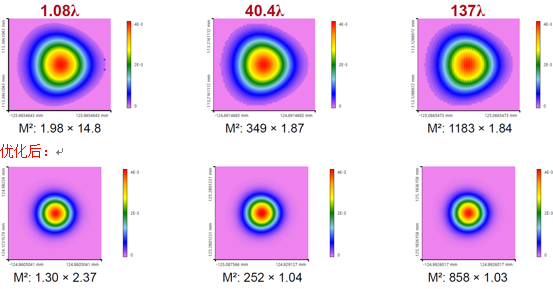 �/2V��'�,0 5)NfZN#�&�
�/2V��'�,0 5)NfZN#�&� 由于波前差和因此校准的偏差更大,M2值明显增加。可以使用高斯孔径来减少。
CIvT�5^}� >��5:e1a?9 总结 V+���~�2q= moI<b\��G@ 实现并分析高性能离轴和无色散反射光束整形装置。
l�c(iy:�z@ 1.模拟 "8�TMAF|i4 通过使用光线追迹来验证反射光束整形设置。
�ly5L-�=Xb 2.研究 Zo��ReyY�2 为了计算场分布和评价光束参数,应用几何场追迹+(GFT+)引擎。
ddhTr�i'f 3.优化 �Y6;9j=�[� 通过使用显示出高斯整形孔径函数和经典场追迹引擎来优化M2参数。
>�mSl~�.I2 4.分析 %�9)�J-��B 通过应用蒙特卡罗公差来分析取向偏差的影响。
*��!s?hHv� 可以使用VirtualLab Fusion非常有效地模拟和分析复杂的光束整形装置,尤其是离轴系统。为此,根据情况应用不同的模拟引擎。
�+Z(VWu��6 DOU?e9I2�� 参考文献 $^ dk>Hj>4 [1]M. Serkan, H. Kirkici, and H. Cetinkaya, “Off-axis mirror based optical system design for circularization, collimation, and expansion of elliptical laser beams”, Appl. Optics 46, No. 22, 5489-5499 (2007).
YV�p0�}m� b:�I5�poI3 进一步阅读 Y�a�epy3F �Px&Mi:4tG 进一步阅读 �Pg C]@Q�% 获得入门视频
z�b�)�S�lR - 介绍光路图
.J�Ka�C>oX - 介绍参数运行
BQf+1�Ly&� 关于案例的文档
@CUDD{1��o - BDS.0001: Collimation of Diode Laser Beam by Objective Lens
�TL:RB)- < - BDS.0002: Focus Investigation behind Aspherical Lens
z�{WqIC�nb - BDS.0003: Optimization of a Lens Doublet for Laser Beam Focusing
[�M>_(u6� - BDS.0004: Focal Beam Size Reduction by Generating a Bessel Beam using Axicon Pair
�T`[ZNq+${ cSDCNc*�%� ~ZN9 �E-uL QQ:2987619807