光束传输系统(BDS.0005 v1.0) =gZA�9@]W2
mDuS-2G=D�
二极管激光光束使用无色散离轴反射装置进行准直和整形 7>AM��zNj
��i�#*l�K7
by,�3���A� e���]{=#�
简述案例 =&�DuQvN�, 5��%@~"YCo 系统详情 �=h�I�;5KF 光源 ���$)6M@S� - 强象散VIS激光二极管 4�sC)hAx&f 元件 :H:�+XIgoR - 光束准直和整形的反射元件(例如圆柱抛物面镜) TnQW���~_: - 具有高斯振幅调制的光阑 W�y /5Qw~s 探测器 h&~9?��B�� - 光线可视化(3D显示) ~b4k�V)[ q - 波前差探测 ^a�1k"|E?f - 场分布和相位计算 �]a[�2QQ+g - 光束参数(M2值,发散角) �Uo�S�c<h| 模拟/设计 I�\I�D��t~ - 光线追迹(Ray Tracing:):基本系统预览和波前差计算 �'rVB2
`z- - 几何场追迹+和经典场追迹(Geometric Field Tracing Plus (GFT+) & Classic Field Tracing): D/�,(xW�aT 分析和优化整形光束质量 �n{M�-t@r7 元件方向的蒙特卡洛公差分析 �JE��<��h� k�X)*:��~* 系统说明 �h�*3{IHAQ �oE0~F|(\1 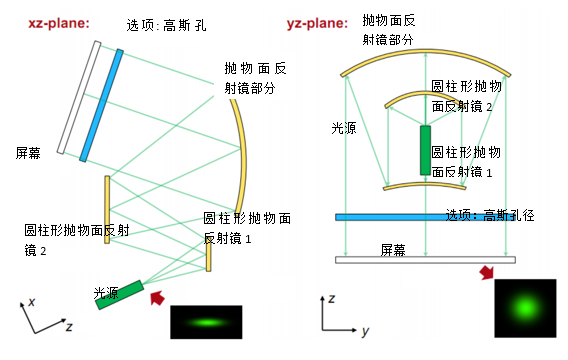 O]@s`����w 模拟和设计结果 ^)a��j,�U[ �0}'/�3Q��
O]@s`����w 模拟和设计结果 ^)a��j,�U[ �0}'/�3Q�� 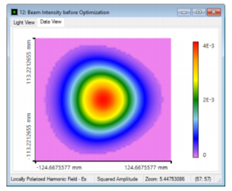
 t5�P8�?q\
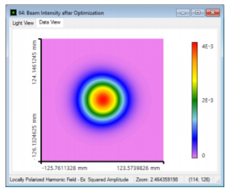
t5�P8�?q\ 场(强度)分布 优化后
DU�g���[L�
 j*d+WZm8-g
j*d+WZm8-g
 �S9���'Xsh M�f7
[�@#$ 总结 �*uKYrs� [
�S9���'Xsh M�f7
[�@#$ 总结 �*uKYrs� [
a^Q
?K\c4N 实现和分析高性能离轴和无色散反射光束整形装置。 �[����e�{D 1.模拟 �t oM+Bd:Y 使用光线追迹验证反射光束整形装置。 gN*���b~&G 2.评估 Q9;VSF�)� 应用几何场追迹+(GFT +)引擎来计算场分布和评价光束参数。 u��h>"TeOi 3.优化 t%@u)�b��p 利用一个具有高斯形状孔径函数的光阑和经典场追迹引擎来优化M2参数。 +G,�_|C2J� 4.分析 abS���3hf� 通过应用蒙特卡罗公差来分析方向偏差的影响。 ]Z�52�L`k �O�h,Xjel� 对于复杂的光束整形装置,特别是离轴系统,可以使用VirtualLab来进行高效的模拟和分析。模拟过程中,根据情况应用不同的模拟引擎。 ��*_H]?&�� �xm�fZ5nVL 详述案例 ,8cVv�->u/
&��[N_{�O| 系统参数 05
.EI�)7 vJsg6�o�H 案例的内容和目标 �P:�5vS:s?
i<q_�d7-W' 在BDS.0001,BDS.0002,BDS.0003和BDS.0004案例中,研究了折射光束传输系统。 $��if(n|�| J*AYZS-tSE  I��OJLJ
p�
I��OJLJ
p�
S>Gb
Jt(�] 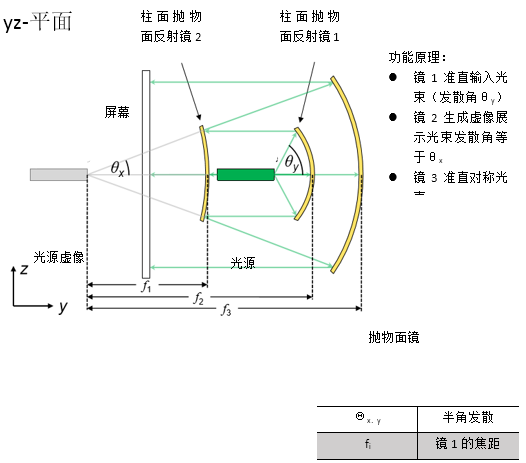 �b'�vIX<
g d ]�#`?��}
�b'�vIX<
g d ]�#`?��} 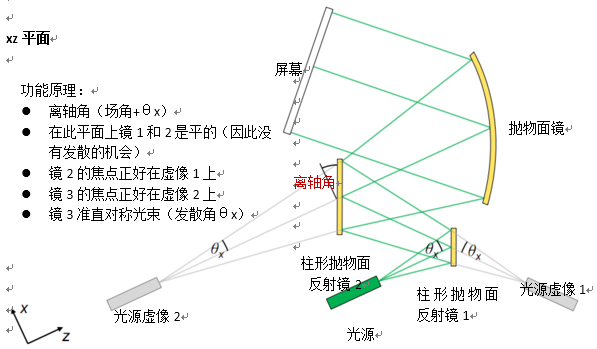 =�)x+f/c] �:�?>yi�7w 规格:像散激光光束 V?-��2F�K] y I[kaH�"J 由激光二极管发出的强像散高斯光束 U9��9Un�y9 忽略发射区域在x和y方向可能发生的移动 V >~�\~H2Y
=�)x+f/c] �:�?>yi�7w 规格:像散激光光束 V?-��2F�K] y I[kaH�"J 由激光二极管发出的强像散高斯光束 U9��9Un�y9 忽略发射区域在x和y方向可能发生的移动 V >~�\~H2Y
de�f\=WyK�  �o��
�WAy[
�o��
�WAy[
1O1��MB&5%
 v+( P�4f�S 9V;�A�+�d,
v+( P�4f�S 9V;�A�+�d,
规格:柱形抛物面反射镜 JIf.d($
~: phwBil-vUU 有抛物面曲率的圆柱镜 *Xn6�y��L9 应用用锥形常数.-1来实现锥形界面 x�1"�8K��� 曲率半径等于焦距的两倍 `3z6y&�dmx
=NWzsR�l, @� 0�/EKWF 规格:离轴抛物面圆柱镜(楔型) �!wZIX�peL zh�Y]����! 对称抛物面镜区域用于光束的准直 ;{0%��V�p{ 从VirtualLab元件目录使用离轴抛物面镜(楔型) q�2;CvoF 离轴角决定了截切区域 t Q�.%f�:| 9"�}5jq4*� 规格:参数概述(12° x 46°光束) D4?cnwU� "
BU4\Q�F- 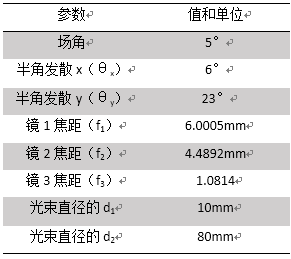
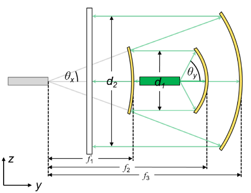 162�Dj�$� cs�[n�FfM� 光束整形装置的光路图 �x V�w�1�� 3ik~PgGoKQ
162�Dj�$� cs�[n�FfM� 光束整形装置的光路图 �x V�w�1�� 3ik~PgGoKQ 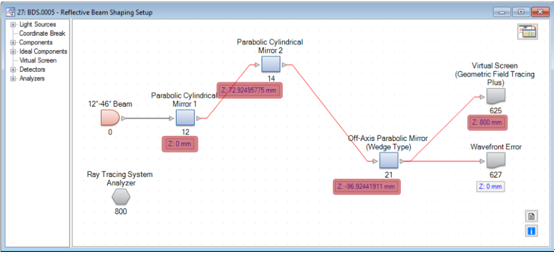 �cqcH�1aSv
�cqcH�1aSv
H;+98AIy`�
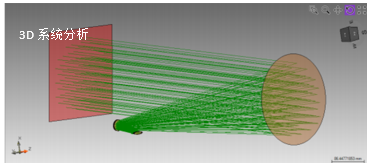
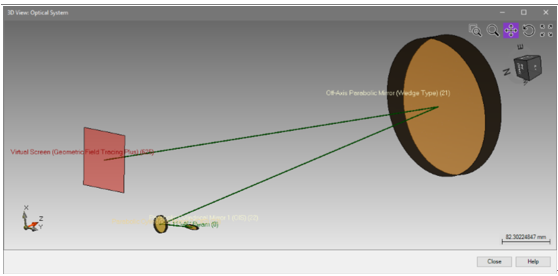 ��n�-����1 ViUx^e\��� 光学元件的定位可以通过使用3D系统视图来显示。 .sb��0|3�& 绿线表示生成的光轴,由VirtualLab的基础定位方法生成(仅仅设置了距离z和倾角)。 '�u�_j�5�� |ly�s�pD�� 详述案例 �+;bZ(_ohG �gb}ov*��* 模拟和结果 p�i/&WMZ�< 3@1$�y`SN� 结果:3D系统光线扫描分析 �&��
�sXMB 首先,应用光线追迹研究光通过光学系统。 o<5+v^mt#� 使用光线追迹系统分析仪进行分析。 �lQ4$d{m`� *g4��Uo�{� file used: BDS.0005_Reflective_BeamShaper_01_RT.lpd ��Bm6t�f}8 +KOhD�tLMG 使用参数耦合来设置系统 *r|1��3�|k
��n�-����1 ViUx^e\��� 光学元件的定位可以通过使用3D系统视图来显示。 .sb��0|3�& 绿线表示生成的光轴,由VirtualLab的基础定位方法生成(仅仅设置了距离z和倾角)。 '�u�_j�5�� |ly�s�pD�� 详述案例 �+;bZ(_ohG �gb}ov*��* 模拟和结果 p�i/&WMZ�< 3@1$�y`SN� 结果:3D系统光线扫描分析 �&��
�sXMB 首先,应用光线追迹研究光通过光学系统。 o<5+v^mt#� 使用光线追迹系统分析仪进行分析。 �lQ4$d{m`� *g4��Uo�{� file used: BDS.0005_Reflective_BeamShaper_01_RT.lpd ��Bm6t�f}8 +KOhD�tLMG 使用参数耦合来设置系统 *r|1��3�|k
T�^ #��1T$
f*^��b�V�_
自由参数: �"5<YN�#
反射镜1后y方向的光束半径 Z�bH_h]1$D
反射镜2后的光束半径 =��!�/T4Oo
视场角,这决定了离轴取向(这些值保存为全局变量) ;� �NO#�/�
由于功能原理,所有系统参数(距离,焦距,直径)可以由光束参数分析计算。 Wxi;Tq9C@_
对于此计算,应用了嵌入的参数耦合功能。 �]��
��^J
(�.�b!k�fC 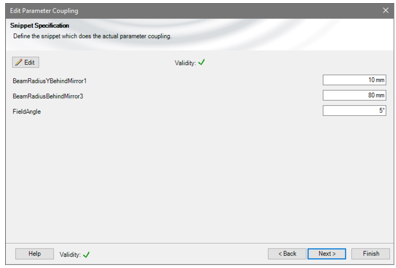 �� J@�J`�)
�� J@�J`�)
�N��1U.1~U
�IN�R��R�A
 v2YU2��-X[
v2YU2��-X[
OK
z5;#�S= 自由参数: xJO�p�~fKG 反射镜1后y方向的光束半径 x@�x5|8:ga 反射镜2后的光束半径 sBNqg~HwB? 视场角,这决定了离轴取向(这些值保存为全局变量) 0;w8���4>M 基于光束发散角和直径(x和y方向)焦点,可以计算并设置反射镜的直径和距离z。 �bvT$/�(7� 8SCXA��9�} T�7����(d� 如果这个例子评估20个参数,那么返回到光路图(LPD)。
msOE�#QL6a EWWCh��0
{ u5`b"��)a 结果:使用GFT+进行光束整形 -:�Q�"aeC5 ���GZmfE�` 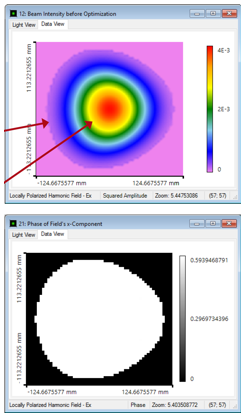 tw���]��
l k��h�Q�fLA q~{O^,4�S�
tw���]��
l k��h�Q�fLA q~{O^,4�S� 现在,利用几何场追迹+计算生成的光束剖面。
�W�I�SK-�z JYLAu�4s6 drp< f1`l8 由于离轴设置,光线分布显示出轻微的不对称形状。
59V8cO+q�H .{�(gku>g( 不过,场分布几乎是对称的(最好是使用伪色(false colors))。
F#RtU �:R� =n;LP#(h�? 产生的相位是完全平坦的,产生的波前误差:
H8E#r*�"-m S�5�cs(}Bq  ;U?���323Z i3>_E� <"9
;U?���323Z i3>_E� <"9 file used: BDS.0005_Reflective_BeamShaper_01_RT.lpd
�vI(CX]�o� nr&9\lG]G� 结果:评估光束参数 :2~2�j-�m
�9q2�x�} /K�lSI<�T@ 从生成的整形光束场分布,可以评估光束参数。 可以直接通过使用探测器界面实现。
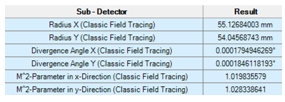
H��YN�p�vK 在这个例子中,我们对光束半径,发散角和M2值感兴趣。
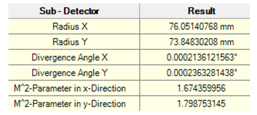
1(��[?E�fC  _�z�npzr9H �/�8����/N
_�z�npzr9H �/�8����/N 整形光束在x和y方向上显示了一个几乎相同的半径。 发散角大约是4urad。
%)e&"mq!| M2值明显高于1。(与理想高斯光束相比,高M2值是由光束偏离引起的)
 �w4�RtIDW: Z0�M|B�v9_
�w4�RtIDW: Z0�M|B�v9_ file used: BDS.0005_Reflective_BeamShaper_02_BeamShaping.lpd
�-�8�S�Z}J 3RI�%O�CGF 光束质量优化 uzS;&�-nA� �r6nW�rO>y %htwq�]rZd 通常,使用合适的高斯调制光阑以用于优化M2值。 因此,我们使用测量的半径作为腰束半径(消除发散角)来生成一个高斯光束。
�k?_���u�v 之后,将接收场转换成一个透射函数。 将该传输函数用作光阑(在一个透射函数元件中)。
*(sv5c!0M8 Y*S(�u�qM� 结果:光束质量优化 ��];QX&";Z ;�Ji3|=�4u "_\77cqpTh 由于通过高斯孔径传播,光束显示出理想高斯形状。 因此,M2值在两个方向上几乎都是1。
Fy�V� $`c$ mzf^`�/N�O 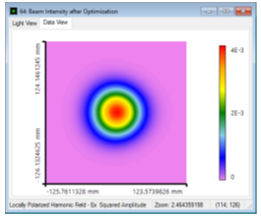 d �0�:;IUG Gw�m�YhG<{
d �0�:;IUG Gw�m�YhG<{ 然而,光束半径是略有减少。(光束半径显示在最后一张幻灯片是由于其偏离了理想高斯。)
�{=+�'3�p� �:=K�+~�?
 JE;!�~�=��
JE;!�~�=�� file: BDS.0005_Reflective_BeamShaper_03_BeamOptimization.lpd
�Z_Y gV:jc O�#�)Y�baE 反射镜方向的蒙特卡洛公差 eq���yUI|e �&#'�.�I0n 对于公差,在随机模式下我们使用参数运行特性。
Q�776cj^L� g,f��
AV�M eX'V#K�#C 这意味着参数变化是的正态
U<����"k�- L(HAAqRn�J 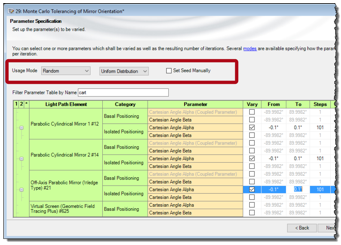 �pwNF\� ={ 2UTmQO��m� .��nei9Y*�
�pwNF\� ={ 2UTmQO��m� .��nei9Y*� 对于这个例子,假设每个反射镜都有±0.1°的角度偏差(绝对的方向)。 由于这个偏差,整形光束的波前差明显增加。
nMBF/75�� 这意味着,波前对对齐误差很敏感。
]'0}��fu�V /7W�dG)'� 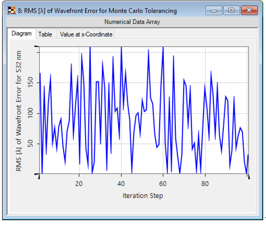 �+�_ �$!9m N �\woFr�G
�+�_ �$!9m N �\woFr�G file used: BDS.0005_Reflective_BeamShaper_04_Tolerancing.run
�3k:`7E.�� 12}!o�S~�_ 第一个随机公差的典型强度分布:(相应的均方根波前差:1.08λ,40.4λ,140λ)
OK�
��\9�` �(?[%u�0%_ 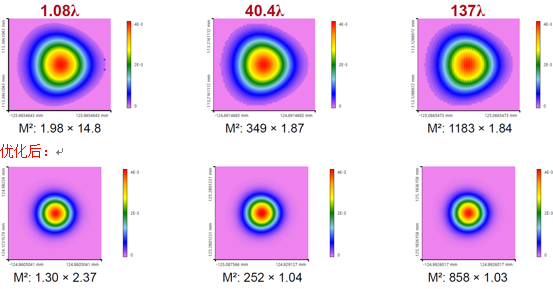 ��z����:A_ �)J
��8mn*
��z����:A_ �)J
��8mn* 由于波前差和因此校准的偏差更大,M2值明显增加。可以使用高斯孔径来减少。
S��|m|�ulB a@C}0IP�)� 总结 e8k|%m<�Sp xr31<��4B� 实现并分析高性能离轴和无色散反射光束整形装置。
~8)l/I=`); 1.模拟 pzT`.#N:M� 通过使用光线追迹来验证反射光束整形设置。
L^�Fb;sJYI 2.研究 k�:��z)S�w 为了计算场分布和评价光束参数,应用几何场追迹+(GFT+)引擎。
}RUK?:l�EA 3.优化 r(g#��3i4Q 通过使用显示出高斯整形孔径函数和经典场追迹引擎来优化M2参数。
9x#T��j/5% 4.分析 �)~� ^`[` 通过应用蒙特卡罗公差来分析取向偏差的影响。
e[db?f�2!� 可以使用VirtualLab Fusion非常有效地模拟和分析复杂的光束整形装置,尤其是离轴系统。为此,根据情况应用不同的模拟引擎。
K�#R|G�Ewr `X(H,Q�}*; 参考文献 �/wi/�i*;A [1]M. Serkan, H. Kirkici, and H. Cetinkaya, “Off-axis mirror based optical system design for circularization, collimation, and expansion of elliptical laser beams”, Appl. Optics 46, No. 22, 5489-5499 (2007).
##s�:��Ww ��V�%��voe 进一步阅读 ��3.h����0 >oapw�5~�5 进一步阅读 !#PA#Q|cO 获得入门视频
@�u:�q��#b - 介绍光路图
�OZ&SxR%q4 - 介绍参数运行
UW{C�`^?=B 关于案例的文档
-v9x t�N�g - BDS.0001: Collimation of Diode Laser Beam by Objective Lens
�}w�C=p>zA - BDS.0002: Focus Investigation behind Aspherical Lens
~NI�qO4 D� - BDS.0003: Optimization of a Lens Doublet for Laser Beam Focusing
af&P��;#�U - BDS.0004: Focal Beam Size Reduction by Generating a Bessel Beam using Axicon Pair
�7s��0pH+� }�5�}#�QHF �U[hok�wZ� QQ:2987619807