摘要 w+Oo-AGN�H
gI5Fzk@�: 本文讨论了基于太空太阳望远镜反射镜单元的光学设计、杂散光和表面粗糙度的要求和光机设计。一些所需的性能参数和理论模拟已经给出,并通过实验结果显示,满足了预期的要求。 �&60�#y4�� ��7���nl� 1. 简介 >XU93 )C�X
^�2<nn op 这里呈现了ESA/NASA太阳轨道任务望远镜反射镜单元的设计历程。该任务致力于太阳和日光层,并被选为ESA宇宙视觉2015-2025计划的第一个中级任务。航天器将会携带各种科学装备。加载在它们其中的一种成像遥感仪器是偏振和日震成像仪(PHI)。PHI仪器将会在可见光的范围内提供光球矢量磁场和视线速度的高分辨率和全盘测量。LOS线速度地图将给出太阳内部详细的日震调查,特别是太阳对流区。通过靠近及从高纬度到35°的位置高分辨率研究太阳,PHI将会处理和解决太阳物理的基本问题。它由两个望远镜组成。离轴Ritchey-Chrétien(RC)高分辨率望远镜(HRT)将会在距离近日点150km处的分辨率下形成太阳圆盘的局部像。折射全盘望远镜(FDT)可以在轨道的各个阶段成像全部太阳圆面。每个望远镜在光路的前面都有自己的偏振调制包(PMP),来最小化偏振串扰效应。在103信噪比水平上的偏振测定是PHI的基线。HRT和FDT会依次将光送入到Fabry-Perot过滤器系统(约100mÅ光谱分辨率)和一个2048×2048像素的CMOS传感器上。太阳日光层的图像如图1所示。在右边中心可以看到一个太阳黑子。此外,日面上的米粒清晰可辨,它们具有几百到1000km的直径。 Kc#42�C;t/ y&�(�R1Y75 图1.太阳光球层的图像
�_[�p@V_my 下面的模型理论意在反射镜单元的设计。首先,如在FE分析中预测的一样,创建一个样机模型(QM)来检验反射镜的机械、热学和光学性质。这包括比如在休息和操作期间超出预期负载的振动测试,来证明设计的可靠性。这些测试成功完成后,两个飞行模型已经建好,可以预见,它们将会集成在飞行模型中又叫做PHI仪器飞行备用零件。 i�J%`y�m4Y O8<�@+xlX� 本文的结构如下。在接下来的部分中,呈现了望远镜的光学设计,为两个反射镜建立了波前预算,以确保在操作条件下所需的光学性能。第一个干涉测量显示了几乎完美的表面。反射镜的表面粗糙度和它对光学成像的影响在第三章讨论。随后是反射镜单元的光机设计的展示。这里呈现了有限元分析的一些结果,并与振动测量的结果作比较。一个简要的总结概括了这方面做出的贡献。 !fT3�mI6u\ 4�+�2hj�*I 2.光学设计和性能 �yS"�;
�q
�^BN?iXQhN 本文的重点是PHI-HRT的光学和光机的设计。光学设计的草图如图2所示。望远镜由一个主凹面和次凸面镜组成。系统的入瞳直径是140mm。主凹面是抛物线型,而次凸面是双曲型。望远镜的焦距是2475mm。仪器工作在617.3nm的Fe线上,谱宽是30nm。视场是尺寸为±0.14度的矩形。由于望远镜没有实际的中间焦点,进入到入射光瞳的辐射能量需要通过一系列渐晕光阑停止下来。要求的分辨率大约为1弧秒,引起最大的总波前误差为λ/25。这给光学和机械设计施加了极限的挑战。为了评估制造以及热学和结构效应对光学性能的影响,运行了一个容差分析,这会产生望远镜允许的偏心、轴向距离变化、倾斜和表面变形的限制。由于围绕太阳的预定椭圆轨道,望远镜需要完全工作在-30°C(远日点)到+90°C(近日点)的温度范围内。为了考虑所有的影响,两个反射镜单元的误差预算已经建立(见表1),误差预算使用波前损耗的各种贡献来评估,如温度变化、装配误差、重力释放和最重要的制造过程,比如光学表面从它的理想形状到抛光相关的偏差。显然,M1带有重力释放的总的预算略微超出规格(WFE<25nm)。然而,这里应该指出,一方面我们已经假定平面外重力(意味着水平安装)最坏的情况为16nm。重力释放更加现实的平面内情况提供了只有2nm。另一方面,我们假定一个相当保守的测量精度为10nm。把这个考虑进去,总的预算很容易下降到25nmWFE需求以下。 tLc~]G*\`s r4wn��f�y� 图2.HRT望远镜的光学设计 �wPRs�.(]_
表1.波前误差预算:M1(左手边),M2(右手边)
iTp�K:p��X 图3.M1基于CGH的NULL光学-干涉仪
\+I+�Lrj�% 此外,通过NULL光学-干涉仪光学方法可以测量反射镜表面,其中计算机生成的全息图(CGH)用于将波前调整为非球面表面形状。M1反射镜的基本实验装置如图3所示。对于M2,考虑其凸面表面,可以使用相似的装置。经过振动测试(见章节4.1),M1-QM反射镜的干涉图如图4所示。测得均方根(rms)波前误差(WFE)是23.9nm。在中心处相当尖锐的梯度位置是人字形-殷钢底座的固定点。它看来在振动测试期间发生了微小的环境效应。通过之前执行的正弦扫描和之后纵轴0dB随机振动测试之间的微小差异可以部分证实这一现象。 ?5�U�b&{��
>=!�$(�JgX �67b[T~92o 图4.M1-QM的干涉图
1}DUe�.�a 可通过在制造和装配过程进一步改善波前,如插入和反射镜锥体的共同研磨,反射镜的性能可以得到极大的提高。FM的干涉图描绘在图5(M1)和图6(M2)中。显然,可以分别实现优良的均方根波前误差值低至为17nm和19nm。因此,对于误差预算(制造+振动)所建立的要求可以用一个舒适的余量来满足。此外,在离子束成形(IBF)、热循环和振动后,由于QM观察的振动载荷导致的表面微小偏差,对于FM反射镜可以避免,对于与干涉图对立的M1反射镜,恰好如图7所示。波前误差只是轻微的下降,要观察的形状没有显著的变化。 H'2Un(#A�l
]>"�q>XgnI \*x��=q�20 图5.振动后M1-FM反射镜的干涉图和泽尔尼克系数
YA'_Ba�(v) 图6.振动后M2-FM反射镜的干涉图
%>�)&QZig/ 图7.M1-FM的干涉图(IBF、热循环和振动后)
��<cx�,Z5W 然后,将测量数据(整数格式)导入到光学设计软件中,并且运行性能分析。用这种方法,可以证实如果调整合适,完成的望远镜能够满足Strehl > 0.8的要求。另外,“完成”的望远镜系统对高质量的反射镜的衍射MTF’s模拟如下所示(图8,左)。作为比较,也为一个在早期抛光不合格的次反射镜的系统模拟了MTF’s,该系统在靠近边缘处显示出严重的波前扰动(图8,右),宽带-均方根(MSF)大约为7nm(见章节3)。当高质量系统的MSF下降到大约1%时,退化的系统显示大约5%,这恰好证实了图9的估计。由于与真实的待观察对象(见图1)已经很低的对比,这是不可接受的。请注意,截止频率准确的计算为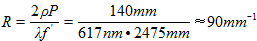 。 �(U@�uJ��� >��^V�3Z{;
。 �(U@�uJ��� >��^V�3Z{; 图8 集成高质量反射镜的望远镜模拟衍射MTF,高质量反射镜-左(图5和图6),和一个具有退化M2的望远镜-右
3^�%sz!jK+ 图 9: 由于MSF粗糙度,望远镜的两个反射镜的MTF下降预测
I]B���[H�6 3. 表面粗糙度 A_}%�Y�Hb� h 1�`yW#%� 对于反射光学系统来说,表面粗糙度尤为重要,因为它直接转化为杂散光光斑[1]。在PHI仪器的HRT部分中,杂散光有许多贡献者。使用功率谱密度(PSD)可以让表面粗糙度得到最好的讨论。球体的光学制造技术具有部分刀具几何形状,可以产生长尺度长度的表面抖动,称之为形状误差。同样,表面断裂力学可以导致短的空间尺度长度的抖动,称之为微粗糙和散射。因此,通常只有两个数字被指定:依据Nijboer Zernike多项式或形状偏差,和用均方根粗糙度给出的表面粗糙度。形状误差已经在先前的章节讨论过。表面(高频)粗糙度通常用显微干涉测量仪器(见下文)。 |@��lVFEl] �d*(wU>J ' 此外,HRT反射镜表面是高阶非球面的。使用现代钻石单转和抛光技术纳米级精度进行加工。最后的抛光步骤通常使用离子束成形技术完成。因此,它们容易引起残留的周期性表面起伏,通常被称为波纹或者中空间频率(MSF)误差。这些误差可能会导致相当大的对比度恶化,尤其是对于像太阳一样的扩展物体的观察,这些特性是特别有害的。因此,需要另一个标准来指定这些表面MSF’s对成像质量的影响。由于MSF粗糙度σ导致的对比度下降可以通过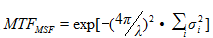 来估计,其中σ是均方根粗糙度[2]。这种特性如图9所示。因此,对于反射镜表面,允许的0.5%的对比度下降会引入2…2.5nm的MSF粗糙度。另外,高空间频率粗糙度适用于微干涉仪范围,即对于0.4/nm到20/mm(2.5倍放大率)粗糙度小于1.5nm,5/mm到500/mm(40倍),粗糙度小于0.8nm。两个放大范围的实验数据已经收集,产生的PSD曲线如图10所示(蓝和红)。然后,在上面使用Harvey-Shack BSDF(双向散射分布函数)进行数据拟合[1,3],最后的参数为b0=80,S=-2.8以及L=0.001(绿色)。 �e�K_Yt~dj K"���U!SWv
来估计,其中σ是均方根粗糙度[2]。这种特性如图9所示。因此,对于反射镜表面,允许的0.5%的对比度下降会引入2…2.5nm的MSF粗糙度。另外,高空间频率粗糙度适用于微干涉仪范围,即对于0.4/nm到20/mm(2.5倍放大率)粗糙度小于1.5nm,5/mm到500/mm(40倍),粗糙度小于0.8nm。两个放大范围的实验数据已经收集,产生的PSD曲线如图10所示(蓝和红)。然后,在上面使用Harvey-Shack BSDF(双向散射分布函数)进行数据拟合[1,3],最后的参数为b0=80,S=-2.8以及L=0.001(绿色)。 �e�K_Yt~dj K"���U!SWv 图10.测量和模拟PSD
�Af��Oq�?V 接下来,使用Photon Engineering 公司的FRED模拟器[4]来运行光学系统的杂散光仿真。在这里,额外的假设需要包含在仿真中。举例来说,机械零件如配件或光阑需要模拟为黑朗伯散射体,这意味着入射光在所有方向散射均匀,具有大大降低5%到10%的反射率。FRED提供了一个预定义的元件用于这个目的,称为黑朗伯体(Black Lambertian)。此外,通过一个等价的表面粗糙度(颗粒效应转变为额外的均方根表面粗糙度)来模拟污染颗粒。根据ESA清洁度规格,微粒子污染洁净度水平CL350等价于500ppm,这需要反射镜表面满足此要求。同样,内场杂散光和外场杂散光都被模拟了。总之,仿真产生约0.1%的内视场杂散光、0.01%的外视场杂散光、由颗粒散射导致的0.16%和有划痕和坑导致的0.2%的杂散光。总计这些结果约为0.5%,满足了低于1%总散射的需求。抛光反射镜的微粗糙度通过微干涉仪检查。最后,用两种放大倍数2.5x和40x研究了4个不同的区域。与规格一致,两个反射镜都可以实现低于2nm的均方根值。M1的一个例子如图11所示。 �.�|Bmg6g*
�.�|Bmg6g*