-
UID:317649
-
- 注册时间2020-06-19
- 最后登录2025-01-24
- 在线时间1672小时
-
-
访问TA的空间加好友用道具

|
摘要 wTL&�m+�xr
+a{P,fRl�@ 光栅结构广泛应用于各种光学应用场景,如光谱仪、近眼显示系统、脉冲整形等。快速物理光学软件VirtualLab Fusion通过使用傅里叶模态方法(FMM,也称为RCWA),为任意光栅结构的严格分析提供了通用和方便的工具。为此,复杂的一维或二维周期结构可以使用界面和调制介质进行配置,这允许任何类型的光栅形貌进行自由的配置。在此用例中,详细讨论了衍射级次的偏振态的研究。 Q|O! cE�W/ y7s:B�uyc
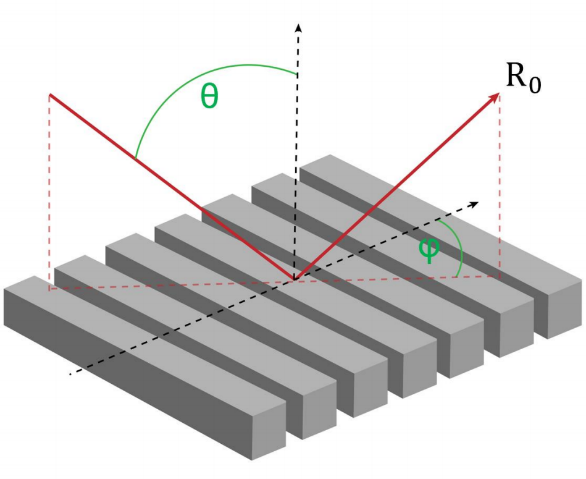 ��^D{!!)�O &6�yh4-�(7 任务说明 K)��z!�e;r ~L�yy7�B�9 ��^D{!!)�O &6�yh4-�(7 任务说明 K)��z!�e;r ~L�yy7�B�9 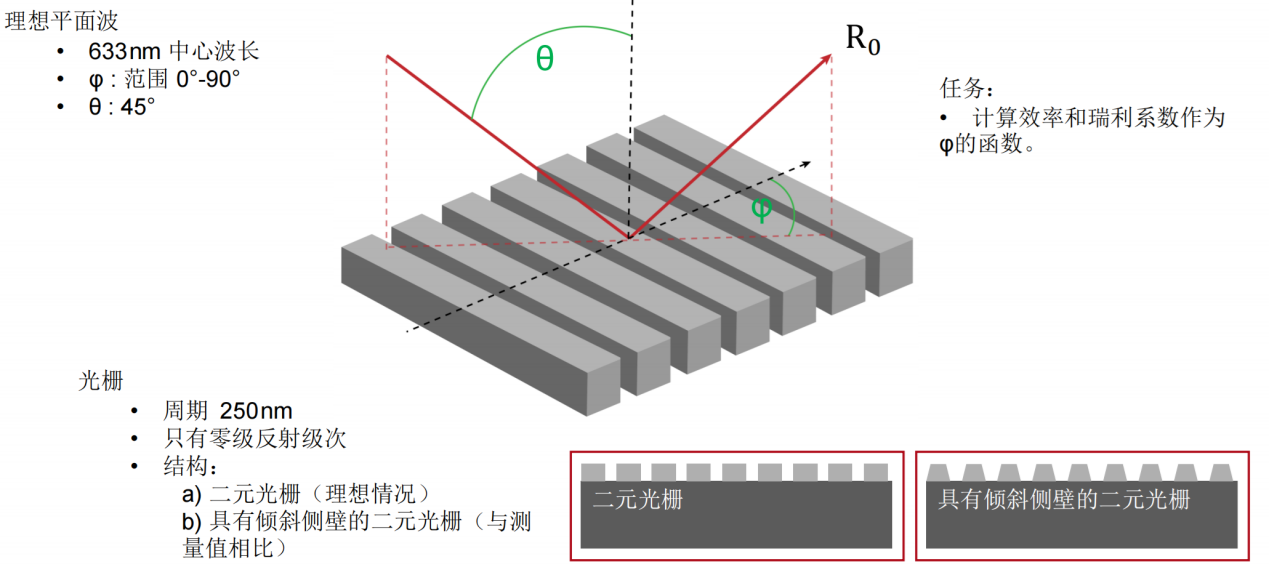 z&�3��i��n ep<O?7@j-G 简要介绍衍射效率与偏振理论 h{��R>L s� 某个衍射级次(𝑛)的效率表示有多少的辐射功率被衍射到这个特定的级次中。它是由复数值瑞利系数计算出来的,瑞利系数包含了每个衍射级次(矢量)电磁场的全部信息。瑞利系数本身是由FMM对光栅的特征值问题进行严格分析的结果。 $Ka-�ZPy<# 如果在TE/TM坐标系(CS)中给出瑞利系数,则可以计算衍射效率: EqN�_�VT�@ z&�3��i��n ep<O?7@j-G 简要介绍衍射效率与偏振理论 h{��R>L s� 某个衍射级次(𝑛)的效率表示有多少的辐射功率被衍射到这个特定的级次中。它是由复数值瑞利系数计算出来的,瑞利系数包含了每个衍射级次(矢量)电磁场的全部信息。瑞利系数本身是由FMM对光栅的特征值问题进行严格分析的结果。 $Ka-�ZPy<# 如果在TE/TM坐标系(CS)中给出瑞利系数,则可以计算衍射效率: EqN�_�VT�@ 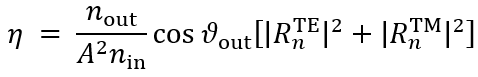 "��-pQL )f 其中,n_in/n_out为覆盖层和衬底层的折射率,ϑ_in/ϑ_out为所分析的阶次的入射角和衍射角。此外,𝐴表示辐射光的振幅。 jmDQKqEc|l 如果瑞利系数沿𝑥、𝑦和𝑧给出瑞利系数,则必须应用以下方程: tY1M�7B�^~ "��-pQL )f 其中,n_in/n_out为覆盖层和衬底层的折射率,ϑ_in/ϑ_out为所分析的阶次的入射角和衍射角。此外,𝐴表示辐射光的振幅。 jmDQKqEc|l 如果瑞利系数沿𝑥、𝑦和𝑧给出瑞利系数,则必须应用以下方程: tY1M�7B�^~ 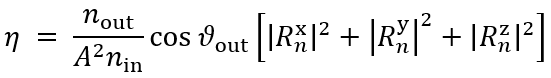 ��;~2RWj=- 因此,必须考虑所给出的瑞利系数的坐标系。默认情况下,光栅坐标系中为 ��;~2RWj=- 因此,必须考虑所给出的瑞利系数的坐标系。默认情况下,光栅坐标系中为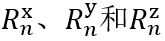 。 W�[dK{?R�B TT�'sO[�N[ 。 W�[dK{?R�B TT�'sO[�N[
光栅结构参数 &<s[(w!%%� 研究了一种矩形光栅结构。 Spn�s��hv8 为了简化设置,选择光栅配置,只允许零阶(R_0)反射传播。 :$>Co\�D�� 根据上述参数选择以下光栅参数: U�^�ec�g{� 光栅周期:250 nm x�}�8 �U\ 填充因子:0.5 #�i8]� �f{ 光栅高度:200 nm rYp]R�X��> 材料n_1:熔融石英(来自目录) �L�=ala1{O 材料n_2:二氧化钛(来自目录) Q*W`m�Fu�l v(=?ge YLo 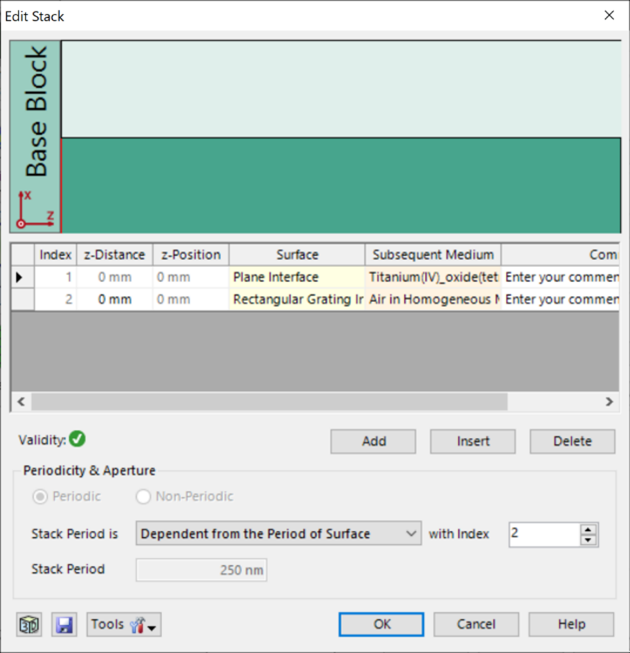 :�r{;'[3�8 *~t&U�x#hj 偏振态分析 8��f""@TTp 现在,用TE偏振光照射光栅,并应用圆锥入射角(𝜑)变量。 H�I`
q!LPv 如前所述,瑞利系数的平方振幅将提供关于特定级次的偏振态的信息。 &�.>
�2��@ 为了接收瑞利系数作为检测器的结果,需要选择光栅级次分析器件中的单个级次输出,并选择所需的系数。 ��O0"u-UX{ �ypCarv�QT :�r{;'[3�8 *~t&U�x#hj 偏振态分析 8��f""@TTp 现在,用TE偏振光照射光栅,并应用圆锥入射角(𝜑)变量。 H�I`
q!LPv 如前所述,瑞利系数的平方振幅将提供关于特定级次的偏振态的信息。 &�.>
�2��@ 为了接收瑞利系数作为检测器的结果,需要选择光栅级次分析器件中的单个级次输出,并选择所需的系数。 ��O0"u-UX{ �ypCarv�QT 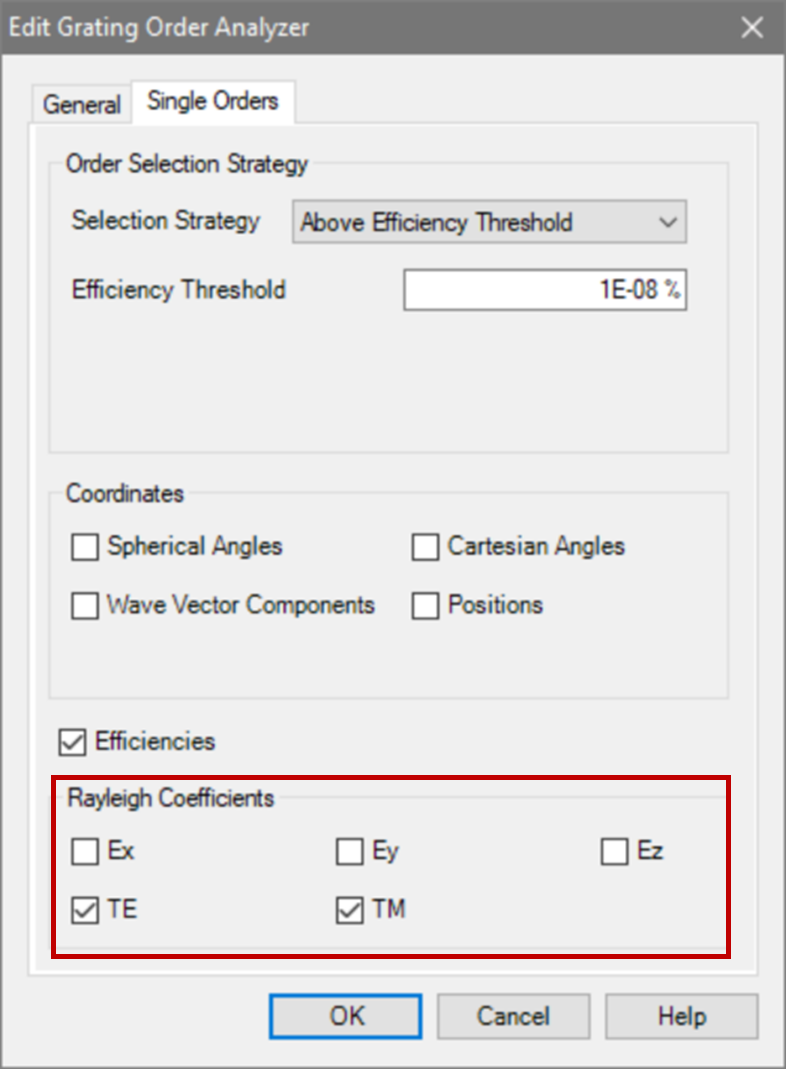 baD`k?]�(� x*Lm{c5��+ 模拟光栅的偏振态 q�qmhh�_[T baD`k?]�(� x*Lm{c5��+ 模拟光栅的偏振态 q�qmhh�_[T
n#�{�z�"G�
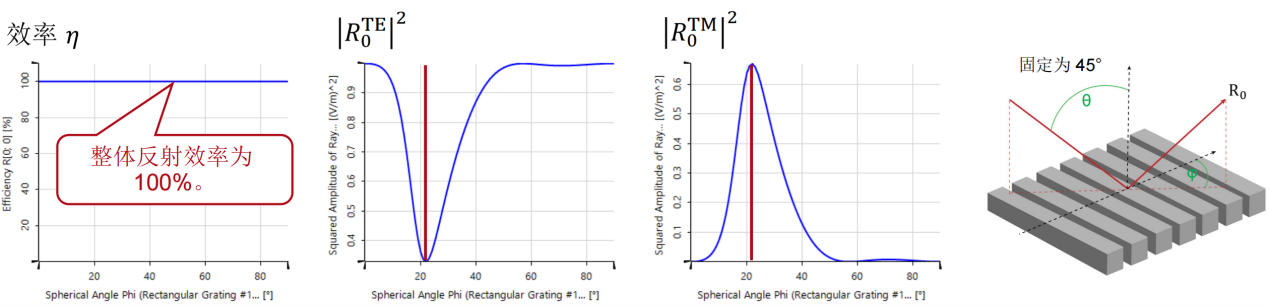 O%���1X[�� e�QiK�\iDS 瑞利系数现在提供了偏振态的信息: xJ�Q-k/` 在圆锥入射角为0(𝜑=0)时, O%���1X[�� e�QiK�\iDS 瑞利系数现在提供了偏振态的信息: xJ�Q-k/` 在圆锥入射角为0(𝜑=0)时,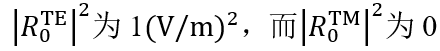 。这说明衍射光是完全偏振的。 #6'x-Z_�� 对于𝜑=22°, 。这说明衍射光是完全偏振的。 #6'x-Z_�� 对于𝜑=22°,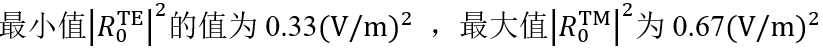 。此时,67%的光是TM偏振的。 +A�
4};]W| 对于𝜑>50°,系数接近为常数,因此偏振态也是常数。 �(}]ae�* D�7�D:?VoR Passilly等人更深入的光栅案例。 k��>2�t�C< Passilly等人的工作研究并优化了亚波长光栅下衍射光谱的偏振态,以获得不同状态之间的高度转换。 �Kx��-s95t 因此,他们将模拟结果与制作样品的测量数据进行了比较。 �z��A�~aiX 。此时,67%的光是TM偏振的。 +A�
4};]W| 对于𝜑>50°,系数接近为常数,因此偏振态也是常数。 �(}]ae�* D�7�D:?VoR Passilly等人更深入的光栅案例。 k��>2�t�C< Passilly等人的工作研究并优化了亚波长光栅下衍射光谱的偏振态,以获得不同状态之间的高度转换。 �Kx��-s95t 因此,他们将模拟结果与制作样品的测量数据进行了比较。 �z��A�~aiX
{Q%�"{�h']
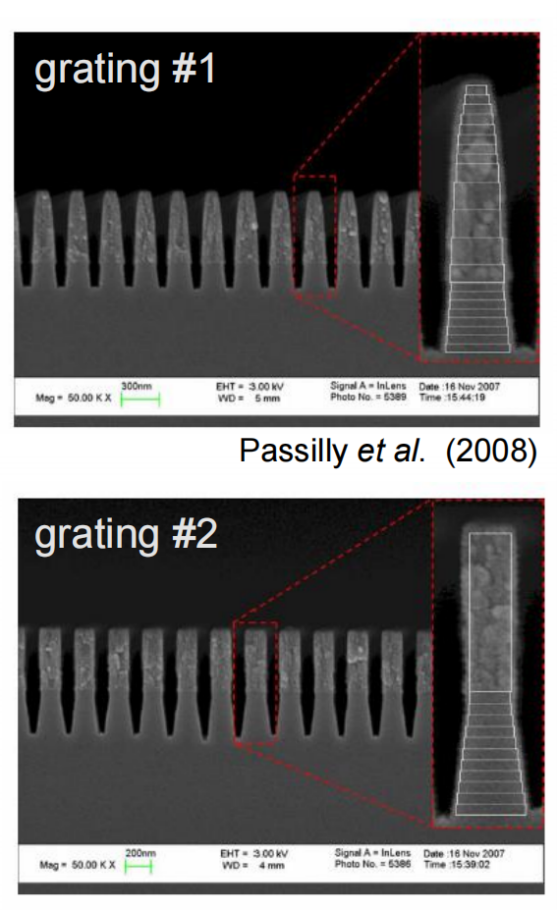
 �]M:=\h,t> =54"��9�*� 光栅结构参数 m�b�ij& 0 在本文中,研究了两种不同的制备光栅结构。 Lrr��1)� h 由于加工造成的光栅的理想二元形状的一些偏差是可以预料的,而且确实可以观察到:在基板和侧壁上存在不完全平行的欠刻蚀部分。 %u��t^� �O 由于缺少关于制作结构的细节,我们将其简化为VirtulLab Fusion中的模拟。 9�kpCn.rJ 但是如果有可用数据,就可以详细分析光栅的复杂形状。 ��#RJFJb�/ �]M:=\h,t> =54"��9�*� 光栅结构参数 m�b�ij& 0 在本文中,研究了两种不同的制备光栅结构。 Lrr��1)� h 由于加工造成的光栅的理想二元形状的一些偏差是可以预料的,而且确实可以观察到:在基板和侧壁上存在不完全平行的欠刻蚀部分。 %u��t^� �O 由于缺少关于制作结构的细节,我们将其简化为VirtulLab Fusion中的模拟。 9�kpCn.rJ 但是如果有可用数据,就可以详细分析光栅的复杂形状。 ��#RJFJb�/
 4Jf6uha��E 4
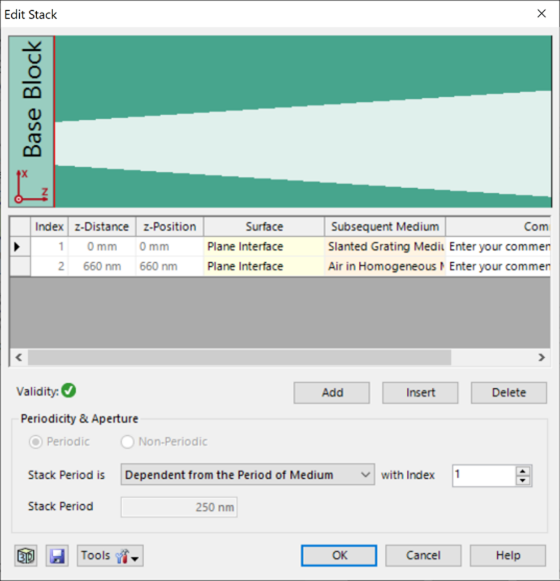
Qo�(�Wl� 光栅#1——参数 �w7(j��SPB 假设侧壁倾斜为线性。 bv%��A��;� 忽略了衬底中的欠刻蚀部分。 �#�QW�G5 为了实现光栅脊的梯形形状,采用了倾斜光栅介质。 "JH�
/�ODm 光栅周期:250 nm zKnHo:�S�V 光栅高度:660 nm >+�9f{FP
9 填充因子:0.75(底部) d�bmt�y|d� 侧壁角度:±6° a*qf\�&Vb| n_1:1.46 �&�
V�*_\� n_2:2.08 8h�Kyp5(%l 4Jf6uha��E 4
Qo�(�Wl� 光栅#1——参数 �w7(j��SPB 假设侧壁倾斜为线性。 bv%��A��;� 忽略了衬底中的欠刻蚀部分。 �#�QW�G5 为了实现光栅脊的梯形形状,采用了倾斜光栅介质。 "JH�
/�ODm 光栅周期:250 nm zKnHo:�S�V 光栅高度:660 nm >+�9f{FP
9 填充因子:0.75(底部) d�bmt�y|d� 侧壁角度:±6° a*qf\�&Vb| n_1:1.46 �&�
V�*_\� n_2:2.08 8h�Kyp5(%l
-0 �e�&>H%
 yV'�<l
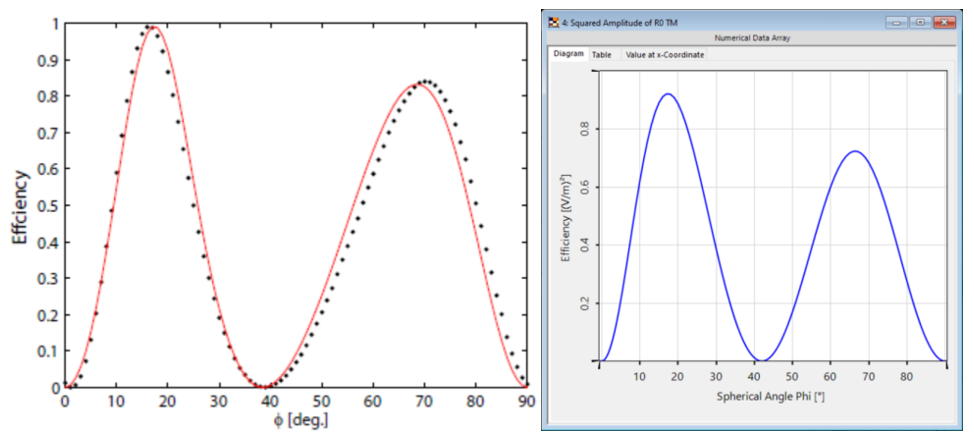
.N ogOUr�J}P� 光栅#1——结果 =GP~h*5es� 这两幅图对比之下匹配度很高,特别是图表的趋势。 2�[O\"a�%� 与参考文献相比,仿真中光栅结构进行了简化,存在一些小的偏差。由于缺乏关于实际的更详细的光栅结构的数据,这种简化是必要的。 j06X�z�\�c �_ ?\4k{ET yV'�<l
.N ogOUr�J}P� 光栅#1——结果 =GP~h*5es� 这两幅图对比之下匹配度很高,特别是图表的趋势。 2�[O\"a�%� 与参考文献相比,仿真中光栅结构进行了简化,存在一些小的偏差。由于缺乏关于实际的更详细的光栅结构的数据,这种简化是必要的。 j06X�z�\�c �_ ?\4k{ET
 �fsA�-}Qc� XOdkfmc+s' 光栅#2——参数 B�9H�a6�kj 假设光栅为矩形。 UC u�4S > 忽略了衬底中的欠刻蚀部分。 B��!;qz[]I 矩形光栅足以表示这种光栅结构。 6���v]y\+ 光栅周期:250 nm �J�frPK/Vn 光栅高度:490 nm u�B�`��H9� 填充因子:0.5 K|OowM4tv� n_1:1.46 �vi�LK\�>> n_2:2.08 U1.w%��b, "��!fvEE�� �fsA�-}Qc� XOdkfmc+s' 光栅#2——参数 B�9H�a6�kj 假设光栅为矩形。 UC u�4S > 忽略了衬底中的欠刻蚀部分。 B��!;qz[]I 矩形光栅足以表示这种光栅结构。 6���v]y\+ 光栅周期:250 nm �J�frPK/Vn 光栅高度:490 nm u�B�`��H9� 填充因子:0.5 K|OowM4tv� n_1:1.46 �vi�LK\�>> n_2:2.08 U1.w%��b, "��!fvEE�� 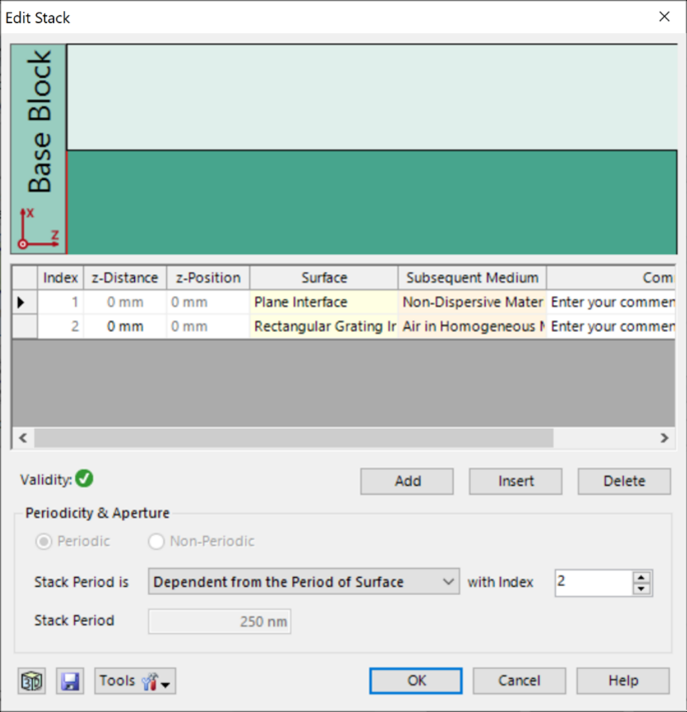 4!I;U�>b b *Dz<P�i�^ 光栅#2——结果 bnm3
cR:h" 这两幅图对比之下再次显示出非常好的匹配度,特别是图表的趋势。 ��ZeL v!� 与参考文献相比,仿真中光栅结构进行了简化,存在一些小的偏差。由于缺乏关于实际的更详细的光栅结构的数据,这种简化是必要的。 3
zF"GT�� �e%B�;8�)7 4!I;U�>b b *Dz<P�i�^ 光栅#2——结果 bnm3
cR:h" 这两幅图对比之下再次显示出非常好的匹配度,特别是图表的趋势。 ��ZeL v!� 与参考文献相比,仿真中光栅结构进行了简化,存在一些小的偏差。由于缺乏关于实际的更详细的光栅结构的数据,这种简化是必要的。 3
zF"GT�� �e%B�;8�)7 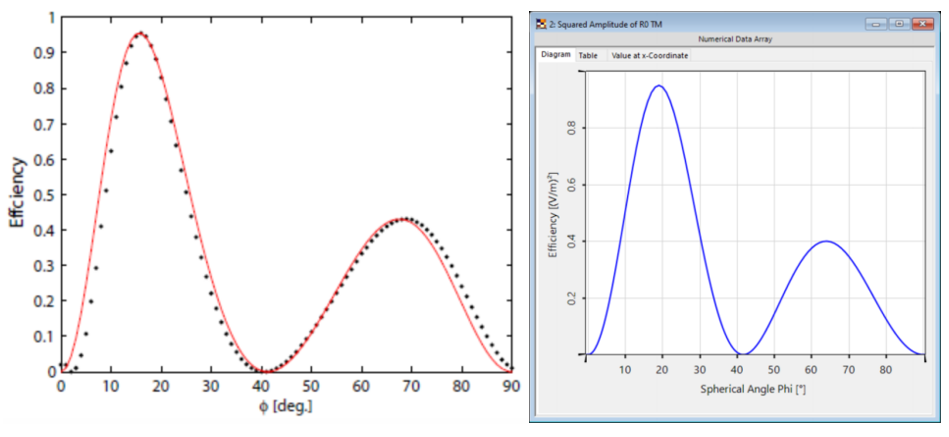 7[�b]%�i� 7[�b]%�i�
|