在JCMsuite中，利用
光学手性的形式和内置的手性参量可以计算光散射体的手性响应。结果表明，时间谐波光学手性密度服从局部连续性方程[1]。这使得手性行为的分析类似于研究电磁能量的
标准消光实验。
xMQ >,nZ Q|+ a 在电磁能量的情况下，消光由散射和损失[2]组成。对应的手性参量是光学手性的消光
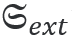
散射
，以及体积
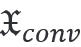
和界面上
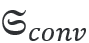
的手性转换。这就得到了守恒定律
#wT6IU1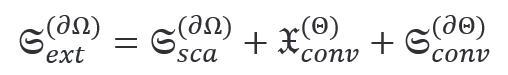 
$Bnc df 积分是在散射体的外表面∂Ω和体积Θ以及表面∂Θ上进行的。
-z .
wAp 6Q>:vQ+E 这些参量在JCMsuite中命名，如下表所示。更多细节可以在这里找到。
'MX|=K!C ,<K+.7,)E 作为案例展示，我们计算散射体的手性响应如下图所示：
6^J[SQ6P V,VL?J\ 它的直径是一个
波长的量级，它的介电常数固定为ε=4.5。在下面，我们将改变散射体的磁导率μ，并观察预测的对偶对称性[3]对于恒定比率ε/μ的散射体及其环境。周围的
材料是ε=μ=1的空气。
T=~d. &J 由于散射体是无损的和各向同性的，在它的体积内将没有转换。请参考四分之一波片的案例，以获得更多关于体积转换的信息。
P-[})Z= 在这里，所需的参量被计算为如上所述的电磁手性通量的通量积分。如下图所示，对于接近对偶对称的材料，转换趋向于零。
ny+r>>3Td 在固定介电常数ε=4.5下，散射体的磁导率μ的变化。
该散射体是对偶的ε/μ=1，产生零手性转换。 6
%aaK|0
&d6ud | 在JCMsuite中，所有手性密度都是相似的。例如，我们在下面的图中展示了增强的近场光学手性密度的
电子部分。这是一个后处理过程，即ExportFields：输出参量电手性密度。
U5-8It2OR 具有ε/μ=1的双散射体的光手性密度X的近场增强 $Yu 'B_E6p
V&ETt.91Ft 参考文献 4qE4 i:b [1] Philipp Gutsche, Lisa V. Poulikakos, Martin Hammerschmidt, Sven Burger, and Frank Schmidt. Time-harmonic optical chirality in inhomogeneous space. In SPIE OPTO, Vol.9756m pages 97560X. International Society for Optics and Photonics, 2016.
+J{ErsG?6P [2] Craig F. Bohren and Donald R. Huffman. Absorption and Scattering of Light by Small Particles. John Wiley & Sons, 1940.
u/|@iWK: [3] Ivan Fernandez-Corbaton. Helicity and duality symmetry in light matter interactions: Theory and applications. PhD thesis, Macquarie University, Department of Physics and Astronomy, 2014.
