案例385(2.0)
0F@�~[W|2� .wD
$Bsm`t 关键字:大角度设计,补偿,枕形,桶形,畸变,强度衰减,信号场准备,
衍射光学元件,损耗,期望光目标图案,迭代傅里叶变换算法
QM#Vl19>j( &hO�-6�(^I 1. 建模描述 ��`hZ�h}K^ 设计扩散器以在远场生成高数值孔径光图案
#|ts1lD#ah
光源参数:
y����$\tqQ — 高斯光源
波长:532nm
= V2Rq�(jH — 根据最终的衍射光学元件选择合适的直径
K<wF�r-�z
系统参数:
u�QKQC��?w — 衍射元件到屏幕距离:z=0.5m
0�M���"n�� 输出场要求:
%�+=;4tH�J — 期望光图案:1.0m×0.5m网格
�7H�5V�zV — 光图案期望分辨率:±0.5mm
�E<��Zf!!3 (目标平面上相邻衍射级次间的最小距离:∆xTP=1mm(离轴))
�DPjs?��M< — 目标图案来源于文件
Zs�
/�>_w} “Sc385_HighNA_DiffuserDesign_01_DesiredLightPattern.bmp”
�
�C3�{hf 衍射光学元件参数:
�@k&6\�1/U — 衍射元件的相位阶数:4
J��<;�i�o! xy7A^7��Li 2. 设计类型与步骤 )�b� �#5rQ -n&&d8G^�s 远场应用
LN��W�S� 优化衍射光学元件用以生成高数值孔径角分布。
b^Z2Vf:k]� ea"X$<s>- 信息 �L@{'����J 衍射光学元件在波数域上生成一个角分布(kx,ky)。
IQ�@��9S�� T��v�DSs]) 设计步骤
h(HpeN%`#� A. 计算衍射光学元件的像素尺寸、周期和像元数。
�/�"�8e�, B. 根据参数计算结果预先设置傅里叶迭代法优化文档。
@����W>@6E C. 根据靶面上期望的光强分布在波数域上生成一个具有预补偿角的光分布,并作为设计目标图形。可以类似的定义一个特定的优化范围。
���l.o/H|� D. 傅里叶迭代法优化文件的最终设置(定义实际的设计目标图案)。
Q3�8+`EhLA A. 计算
�P|<V0
Vs. 1. 根据信号场沿x方向扩展的一个合理的初始值计算衍射光学元件的最小像素(特征)尺寸(此处xmax SF仅有0.75m):
Ze�~�P6�� 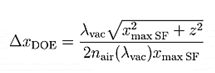 d\Ja�Y�izp
d\Ja�Y�izp 将此值近似到一个可加工尺寸 (∆x’DOE)以兼顾制造者加工过程中对于位置增加以及最小特征尺寸的加工能力。此处近似后,∆x’DOE=320nm。根据
Q;$k?G�=�l 该值重新计算对应的x’max SF值。
J���:N(U0U =G�:Krc8w@ 2. 计算衍射光学元件最大周期 pmax:
N!(mM;1X) 利用公式
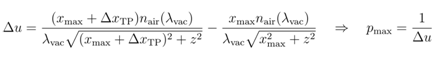 bW6| �&P}X \Nt�
5TG�_
bW6| �&P}X \Nt�
5TG�_ 3. 计算衍射光学元件每个周期的像素数#s和近似给出采样点数目#s’。例如#s’=2355
*'�-4%7C`1 dn#I,x��a` 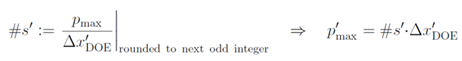 �ua�F�-�3� +d6onO�{�8
�ua�F�-�3� +d6onO�{�8 4. 计算可得到的最大衍射角(用’表示)
�;_I>`h"�r fWmc$r5n]( 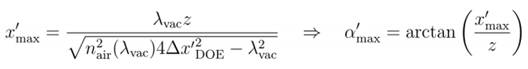 ;D�uV�b2~+ o'#& �=h$_
;D�uV�b2~+ o'#& �=h$_ 5. 计算获得的轴上输出光强的分辨率
M��W�7~�=T �|�reA`&<q 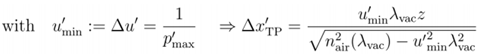 ;�
B�N8�1; o9���9ExQ.
;�
B�N8�1; o9���9ExQ. B. 迭代傅里叶变换方法优化文件的预设置
��R�'k��`0 vTK%4=|1}! C. 1 生成预补偿信号场
�<-v�
zS�; 根据目标平面上给出的空间光强分布,使用模块Mod014在波数域计算一个角谱光强分布。
HD�H�G~<s� 必须在模块对话框中输入采样距离,采样距离可通过迭代傅里叶变换方法优化文件计算出来并以波数值表示(在迭代傅里叶变换方法文件中不勾选“使用角谱坐标”)。
LL#REK|lm8 S[zvR9AW&� C. 2 模块设置
teJt.VA7�) }gkLO
TJ/, 设计波长
]o�<]A�[<� 衍射光学元件与目标平面间距离(需考虑角度要求)
ipwlP|UjQ5 /*��q�RbN� C. 3 模块设置
F0�<�)8�{s 选择扩散器模式
KV_/f�a~Ry V'&;r'#�O� C. 4 模块设置
Ab@�G^SLX� 4�/b��.;$� \_`��qon$9 采样点自动适应选择
Q/S� ^-�&~ 采样距离取自傅里叶迭代算法优化文件
eA4D.7H�DK
视场角以波数坐标形式表示kx,ky
INN��}�xZ� G4@r_�VP�\ C. 5 利用模块补偿
}3{eVc�t#| {�$^�'oRk Vg��m'&Y�T D. 在傅里叶迭代算法优化文档中定义DTP
'dKfXYY1`N |T�|m5�V'l 在IFTA优化文档中,生成的预补偿DTP作为期望输出场。
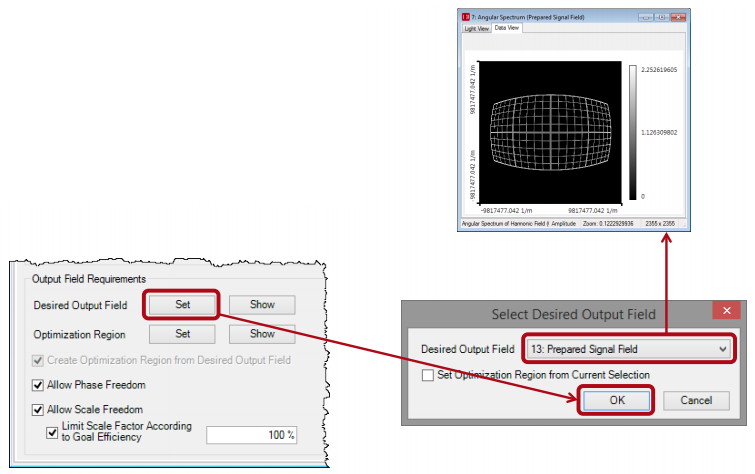 /Q;w��z!V$
/Q;w��z!V$ VirtualLab
软件为用户提供了更便于使用的设计工具,用于设计生成大角度光图形的大数值孔径衍射光学元件。
K�W� .4 9� 典型的不希望的效应:
Oh! {E5�!) — 几何畸变
�9^}&��PEl — 强度衰减
H>C��bMz1u 都可被完全地补偿。