-
UID:317649
-
- 注册时间2020-06-19
- 最后登录2026-02-06
- 在线时间1926小时
-
-
访问TA的空间加好友用道具

|
测量系统(MSY.0003 v1.1) ?#<'w(^%# H(Wiy@�cJn 应用示例简述 -4�Dz9�8du
z|],�s]F>G 1.系统说明 9���a@S^B>
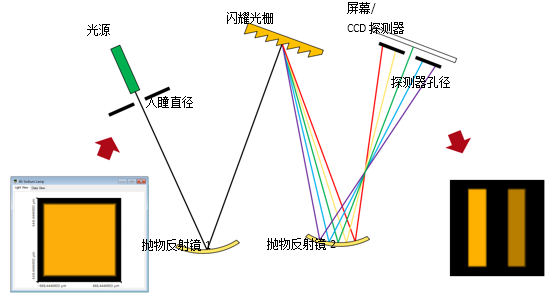
�^��GY�VRD 光源 f'�"PQr^9 — 平面波(单色)用作参考光源 yz,_\{��}� — 钠灯(具有钠的双重特性) ��x ]}�'�H 组件 ' x�aPahx; — 光阑(狭缝),抛物面反射镜,闪耀光栅 �W,�,3�@�: 探测器 $s
,�g&7*- — 功率 q�}��,,[t� — 视觉评估 �%L�)�QTv/ 建模/设计 ~x�4]p|)</ — 光线追迹:初始系统概览 9
4��bDJy1 — 几何场追迹+(GFT+): dg*xo9�Xi` 窄带单色仪系统的仿真 hN0h�'JJ[7 为分辨特定光谱曲线进行整个光谱的高分辨率分析 0n4(�Rj|}2 R$�IsP,Uw� 2.系统说明 O�5:U2o��-
SJc*Rl��>�
 ro�?.w���� F�@ pf�._c 3.系统参数 �\I6F;G��6 ro�?.w���� F�@ pf�._c 3.系统参数 �\I6F;G��6
)#4(4
@R h
 j��p}�.�W� xh<{�lZ)KJ w�ZC�boQ, 4.建模/设计结果 c3rj
:QK6I j��p}�.�W� xh<{�lZ)KJ w�ZC�boQ, 4.建模/设计结果 c3rj
:QK6I
�Hs�ov��0� 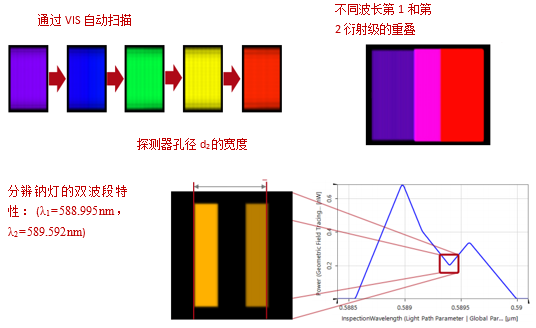 h7�.j�WJTo h7�.j�WJTo
/_expS�PHl 总结 ]C+P��J:CC
t�]v�v&vk> 模拟并分析了Czerny-Turner单色仪及并将其用于光谱研究中。 �@�@R&�OR� 1. 仿真 sm�[zE�/2b 以光线追迹对单色仪核校。 |F�aK��=�e 2. 研究 X�g��USJ�* 应用经典场追迹和几何场追迹+引擎对系统的性能进行研究。系统分析中包括采用傅里叶模态法进行光栅效率的严格分析。 L`��O7-'`� 3. 应用 `B�8`<3k/( 应用真实的Czerny-Turner单色仪分辨了钠灯的双波长特性 �.M�DSP/s 可以通过使用VirtualLab对复杂的光谱系统,比如Czerny-Turner进行详尽的研究。 fpZHE=}��r
\%�}]��wf} 应用示例详细内容 3��AP�=��� 系统参数 |V}t��T�x1
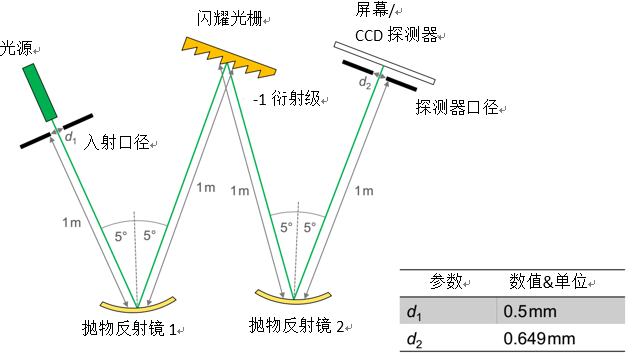
.2rp�Qa/�h 1. 仿真任务:Czerny-Turner干涉仪 p�nuwj��U- Czerny-Turner干涉仪是一种广泛用于光和样本的光谱研究。主要由两个球面或抛物面反射镜、两个光阑以及一个作为分光元件的光栅组成。 �dF�!� B5( p}I\H
^"8+
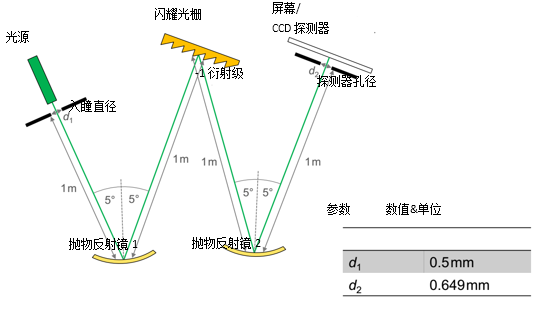
 m4~~��q[�t JX>�`N5�s� 2. 系统参数 M
$EH�x[*5 m4~~��q[�t JX>�`N5�s� 2. 系统参数 M
$EH�x[*5
N48�X[Q��* 元件在1m范围内的距离与非常窄的入瞳孔径进行结合以确保单色仪/光谱仪的高光谱分辨率。 Y)(w��&E>1
�it>l?h7�I
 �KL(s�Vj^e |,T���BP�@ 3. 说明:平面波(参考) �r>KmrU�4Q �KL(s�Vj^e |,T���BP�@ 3. 说明:平面波(参考) �r>KmrU�4Q
�a�A�d1[?&
采用单色平面光源用于计算和测试。 KdTWi;mV2-
1B 0[dK�2N
 �/�UR;,t�s �09Q5��gal 4. 说明:双线钠灯光源 w�Jg�H15oB �/�UR;,t�s �09Q5��gal 4. 说明:双线钠灯光源 w�Jg�H15oB
�!-SI� &qy
_�x$Eq:
�i
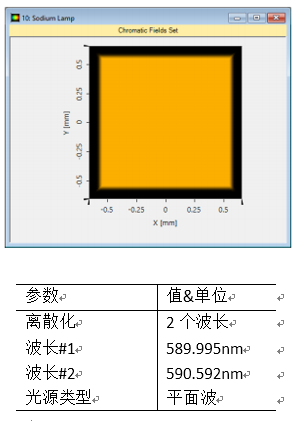
为了增强光谱仪的光谱分辨率,对钠灯的双波长特性进行研究。 z��}����r
双波长通过旋转轨道的相互作用分离,表现为具有515GHz频率差异(波长差为0.6nm)。 hD�oFF8)c�
由于低气压灯的扩展发射区域,钠灯可视为平面波。 a�7b1�c�!�
?<
Ma4yl</
 Gp?pSI,b.t v�y-(:aH7U 5. 说明:抛物反射镜 �X}QcXc.�d Gp?pSI,b.t v�y-(:aH7U 5. 说明:抛物反射镜 �X}QcXc.�d
)��*.�r�l�
��W�kp�He�
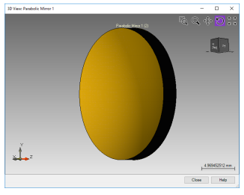
利用抛物面反射镜以避免球差。 r�� M}�o)�
出于此目的,在VirtualLab库目录中选择离轴抛物面反射镜(楔形)组件。 I~ �mu�'�T
�VS~+W�=5}
 �Gt,VSpb~s �Gt,VSpb~s
�]_L���;AD
 NSz�Tl-e�S F,mStw�:� 6. 说明:闪耀光栅 �k0�b�6X5 NSz�Tl-e�S F,mStw�:� 6. 说明:闪耀光栅 �k0�b�6X5
GJ��?J6@�|
'w��/�S6j
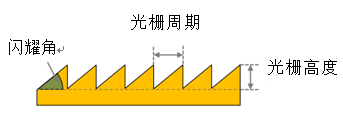
采用衍射元件用于分离所研究光源的光谱波长。 ��B�1�Z��;
通过使用闪耀光栅,可以对期望衍射级次的衍射效率进行优化 o�l�HmRJ��
-Vmp6X�Y3q
 q�c�kRX+P` q�c�kRX+P`
� ME5M;bz(
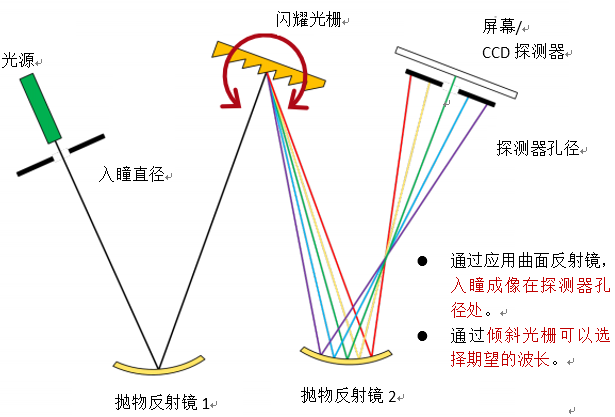
 �7�9�jnYjk Efpj��u( � 7. Czerny-Turner 测量原理 BryD?/}P)M �7�9�jnYjk Efpj��u( � 7. Czerny-Turner 测量原理 BryD?/}P)M
Xo�q���� - 通过光栅倾斜角的变化,入瞳的像可经过探测器孔径进行扫描。探测器可以评估光入射的能量。 `X�i)';�p�
��!"F8jA�}
 %w!x \�U�V ( p�CU:'�" e!k4�Ij-]� 8. 光栅衍射效率 V72?E%�d0 ^%U`|GB�Zp %w!x \�U�V ( p�CU:'�" e!k4�Ij-]� 8. 光栅衍射效率 V72?E%�d0 ^%U`|GB�Zp
vZqW,GDfXo
VirtualLab的光栅组件可通过傅里叶模态法(FMM)对衍射级次进行严格的计算。 :hf%6N='kI
因此,每一个波长的效率可视为独立的。 �wr>�6G�o%
3个不同波长的不用的衍射效率的归一化强度:(可被测量系统的计算视为如此) Psf{~ (Ii�
�i�DsY��5l 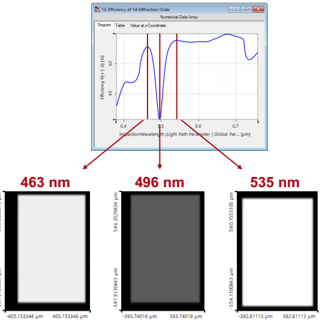 �D�o���N]v file used: MSY.0003_Czerny-Turner_Mono_01_Diffraction_Efficiency.lpd 3r��?�T|>| {uqP�+�Cs� 9. Czerny-Turner系统的光路图设置 �%Go�/\g � �D�o���N]v file used: MSY.0003_Czerny-Turner_Mono_01_Diffraction_Efficiency.lpd 3r��?�T|>| {uqP�+�Cs� 9. Czerny-Turner系统的光路图设置 �%Go�/\g �
XHJ�/2�1�1
 R3#�| *)�q ��{yxLL-5c 由于VirtualLab的相对位置系统,只设置了沿Z轴方向的距离。 ���4�jVd�� #~r+�Z[(,p 10. Czerny-Turner 系统的3D视图 xaq/L��:I< R3#�| *)�q ��{yxLL-5c 由于VirtualLab的相对位置系统,只设置了沿Z轴方向的距离。 ���4�jVd�� #~r+�Z[(,p 10. Czerny-Turner 系统的3D视图 xaq/L��:I<
bc&�� 5*?�
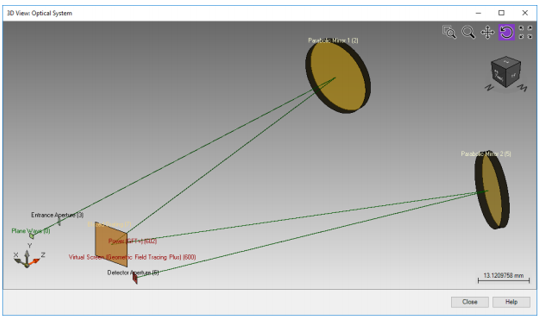 dL1{�i��,M $/E{3aT@F2 增大平面波光源和孔径的距离仅是为了更清晰的显示3D视图(可在光路编辑器中实现)。 z�P$�"6~.� 不仅如此,距离减到0.1倍是为了提高视图的可观察性。 XWB#�7;,�R �Q[T)jo,j% 应用示例详细内容 ki��?V
eFp dL1{�i��,M $/E{3aT@F2 增大平面波光源和孔径的距离仅是为了更清晰的显示3D视图(可在光路编辑器中实现)。 z�P$�"6~.� 不仅如此,距离减到0.1倍是为了提高视图的可观察性。 XWB#�7;,�R �Q[T)jo,j% 应用示例详细内容 ki��?V
eFp
A#F6~QX(.9 仿真&结果 �B�G1�hk�!
�0OtUb:8LX 1. 结果:利用光线追迹分析 Izfq`zS+\s 首先,利用光线追迹分析光在光学系统中的传播。 h�6�:|R�GF 对于该分析,采用内嵌的光线追迹系统分析器。 [XP\WG�>�s
�|uJjO>8]|
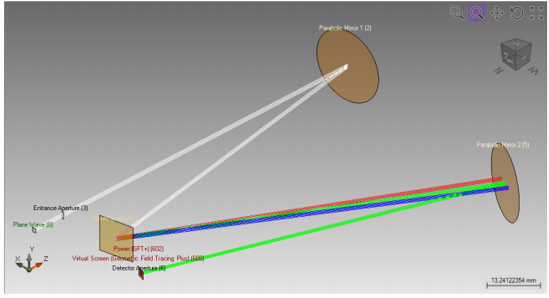 (|tR>R.Wxg DKN�cp�8<J file used: MSY.0003_Czerny-Turner_Mono_02_RT.lpd M'NOM>��8 (|tR>R.Wxg DKN�cp�8<J file used: MSY.0003_Czerny-Turner_Mono_02_RT.lpd M'NOM>��8
E7<l^/<2S+ 2. 结果:通过虚拟屏的扫描 >5�t�]Zlb` 通过将光栅倾斜合适的角度以选择被探测的波长 (可通过光栅方程计算该角度)。 �M����J�n= 采用VirtualLab中的参数耦合功能连接波长和光栅的倾斜角度, - C8VDjf9� 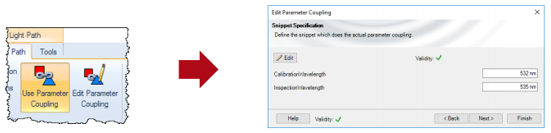 �i`w&{WTRQ 通过该功能给定波长,可以自动设置合适的倾斜角。因此,如为了仿真全谱段,参数运行必须指定波长。 L�*{E�-m/� ��:?)q"h�E �i`w&{WTRQ 通过该功能给定波长,可以自动设置合适的倾斜角。因此,如为了仿真全谱段,参数运行必须指定波长。 L�*{E�-m/� ��:?)q"h�E
 6x16�?�x�� animation: MSY.0003_Czerny-Turner_Mono_03_VIS_Scan.bms v\=k[oOu� 6x16�?�x�� animation: MSY.0003_Czerny-Turner_Mono_03_VIS_Scan.bms v\=k[oOu�
:v�E\r#hJ" 3. 衍射效率的评估 ��:4Y���5 为选择合适的仿真引擎,必须考虑孔径衍射效应的影响。 S�aks~m7,� @|d�`n\�%x
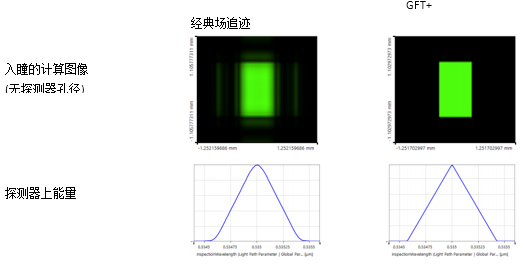 Ma ]*Ple�d 比较经典场追迹和几何场追迹+可知,由于两者的差别较小,可忽略衍射效应。采用更快速的GFT+引擎用于后续研究。 �� {C�%f~j file used: MSY.0003_Czerny-Turner_Mono_03_Diffraction_Effects.lpd e,�*@+E\4 Ma ]*Ple�d 比较经典场追迹和几何场追迹+可知,由于两者的差别较小,可忽略衍射效应。采用更快速的GFT+引擎用于后续研究。 �� {C�%f~j file used: MSY.0003_Czerny-Turner_Mono_03_Diffraction_Effects.lpd e,�*@+E\4
�Jg6@�)�<n 4. 结果:衍射级次的重叠 �-_>E8PhM� 因为光栅用于分离多谱段(如可见光),所以不同衍射级次可能发生重叠。 z
E\~O�a;� VirtualLab的光栅组件可以计算所有期望的衍射级次(包括利用傅里叶模态法计算衍射效率)。 c���fc=a�� 0级衍射并不分散,但2级衍射相对于1级衍射表现出较大的发散角。 X09i�+/ICK 通过光栅参数和光栅方程的计算可发现重叠为760nm(1级)和380nm(2级) NU�3s^ 8\( 光栅方程: iu��`�B8yI
�C�I��|#,^ 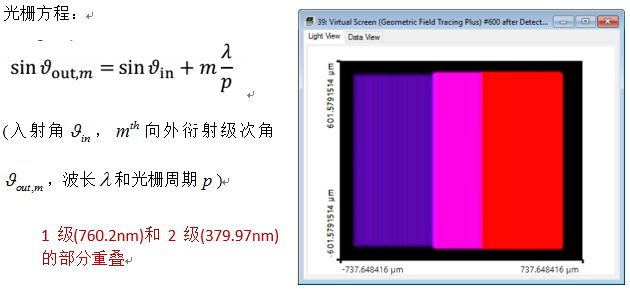 w�!I�i���� �85:mh\@-G ,���,h>_IA 5. 结果:光谱分辨率 22E��I`}"J w�!I�i���� �85:mh\@-G ,���,h>_IA 5. 结果:光谱分辨率 22E��I`}"J
�8HWEO�bRY
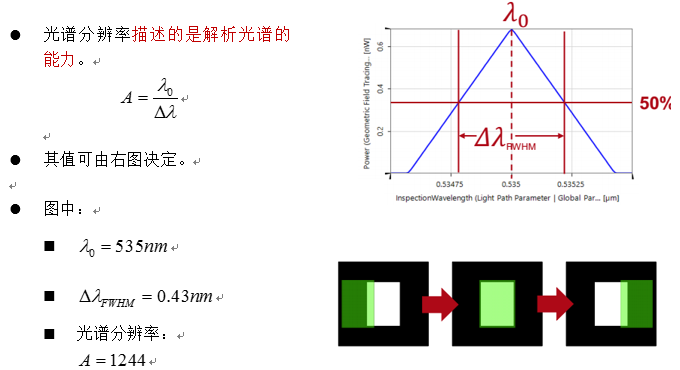 �2KNs,4X@� file used: MSY.0003_Czerny-Turner_Mono_06_Resolution.run 2=n,{rkmj% �2KNs,4X@� file used: MSY.0003_Czerny-Turner_Mono_06_Resolution.run 2=n,{rkmj%
�cM=�_i{�c 6. 结果:分辨钠的双波段 |u[@��g`�Z 应用所建立单色仪分辨钠的双波段特性。 6+SaO
!�lR Gr~J-#a3~D
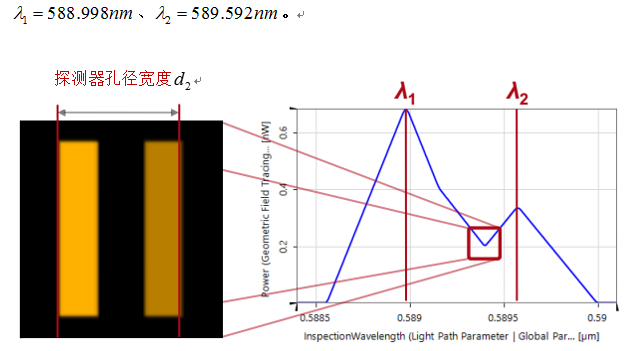 zy8D&7�Ytf zy8D&7�Ytf
E$4I�k��.k 设置的光谱仪可以分辨双波长。 '.X�R,\g>� dF+:9iiA�m file used: MSY.0003_Czerny-Turner_Mono_07_Sodium.run %)y-BdSp�. ���%eJE�@$ 7. 总结 0w6"p>�s>c 模拟并分析了Czerny-Turner单色仪及并将其用于光谱研究中。 F�441��K,I 1. 仿真 N{K[s�XC�W 以光线追迹对单色仪核校。 jj�g[v""3| 2. 研究 2�nI^fVR%\ 应用经典场追迹和几何场追迹+引擎对系统的性能进行研究。系统分析中包括采用傅里叶模态法进行光栅效率的严格分析。 H��� `_{n< 3. 应用 VW**N}�1#C 应用真实的Czerny-Turner单色仪分辨了钠灯的双波长特性 C�=DC �g�� 可以通过使用VirtualLab对复杂的光谱系统,比如Czerny-Turner进行详尽的研究。 D|/
4�)�,v 扩展阅读 �er���2#�h 1. 扩展阅读 Yo,n#<3��7 以下文件给出了在VirtualLab中如何设置测量系统的更多细节。 3�5~1$�uRA ^dKtUH/78G 开始视频 (6i.��>%|_ - 光路图介绍 dz�)(~@tgz - 参数运行介绍 r��f
=W�q_ - 参数优化介绍 ~L9I@�(/�S 其他测量系统示例: � $kY� ]HI - 马赫泽德干涉仪(MSY.0001) p� ���u[S� - 迈克尔逊干涉仪(MSY.0002) p�^ )iC&*0
|