-
UID:317649
-
- 注册时间2020-06-19
- 最后登录2025-12-12
- 在线时间1894小时
-
-
访问TA的空间加好友用道具

|
在物理光学中,我们使用麦克斯韦方程组处理电磁场。为了快速求解该方程组,我们将不同的麦克斯韦算子结合在一个非序列场追迹概念中。进一步的,快速物理光学概念的支柱是:(1)尽可能在k域求解麦克斯韦方程组。(2)根据处于哪一个场域,使用常规或几何傅里叶变换,选择k域或空间域。(3)通过所谓的双向算子仿真光学组件的效应。(4)几何双向算子的引入。这些概念的结合产生了一种物理光学理论,其具有快速建模算法,该算法固有地以定义明确、有说服力的方式应用了几何和衍射模型。 ��<��m3o�r ~�M4@hG�!� 1.场追迹图 s.7�s�:Q`
Lb}
c�jI:� 一个光学系统的麦克斯韦方程组的解可以通过非序列场追迹算法得到[1]。这导致所有通过系统中不同光路的模拟,都由一系列自由空间传播步骤和与空间中非均匀区域,例如光学器件的互作用组成。从光源平面中的场开始,自由空间算子P规定了在下一个组件平面上的场,其中组件的响应由算子B给出。这些算子应用于x域或k域。一个光路的模型可以由所谓的场追迹图说明,图1给出了相应的例子。 }��^R_8{>k 2?b��E2^6� 图1 物理光学中一个光路的场追迹图模型。参数j指明了应用算子的场参考平面。 �=�Y���RN"
尽管电磁场包含六个场分量,场追迹算法仍然可以通过ρ=(x,y),E┴(ρ,ω)=(Ex(ρ,ω), Ey(ρ,ω))正式地表示,缺失的四个分量可以根据E┴的需求计算。在k域中,这些计算遵循简单的代数方程。 �5}�;$>47m 自由空间算子方程由 给出,输入平面场为 ,输出平面(输入平面的下一个算子)的结果为 。如果输入/输出平面不平行,则传播算子P通过衍射积分和附加的倾斜算子表示自由空间中的传播[2]。尽管在空间域中,传播被表示为有大量数值计算成本的衍射积分,但在k域中,对于平行平面和非平行平面的附加坐标变换,我们则有简单的表达式(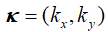 ) '�;0N��WFP ) '�;0N��WFP 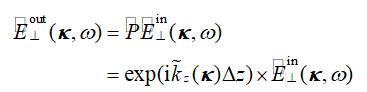 (1) R1=ir# U|D 通过选择常规或几何傅里叶变换[3],可以来回转换k域和空间域,不同的衍射积分遵循空间域中的公式1,包括Rayleigh-Sommerfeld、远场和Debye积分。k域中自由空间传播的简单性是快速物理光学选择k域的一个重要原因。另一个原因是可以从 快速代数计算 和 。下面将介绍场追迹算法中的B算子。 ~�8�
�w(M� (1) R1=ir# U|D 通过选择常规或几何傅里叶变换[3],可以来回转换k域和空间域,不同的衍射积分遵循空间域中的公式1,包括Rayleigh-Sommerfeld、远场和Debye积分。k域中自由空间传播的简单性是快速物理光学选择k域的一个重要原因。另一个原因是可以从 快速代数计算 和 。下面将介绍场追迹算法中的B算子。 ~�8�
�w(M�
.�6D�9m.Q, 2.双向算子 ,� JUP�� �
(&a<�6���k 空间域中我们有B算子 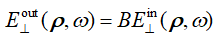 ,并且类似的在k域中有 ,并且类似的在k域中有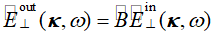 。两个域中的算子都有矩阵形式,例如k域为 OnKP�D�=<� q�4rDAQyPO 。两个域中的算子都有矩阵形式,例如k域为 OnKP�D�=<� q�4rDAQyPO
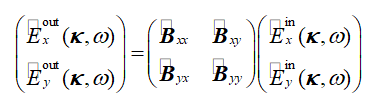 (2) �5Si\hk�:o 这个矩阵中每一个算子都代表一个积分运算符,例如k域中有如下积分形式(忽略ω) &G"�r>,H�U [If��hh��2 (2) �5Si\hk�:o 这个矩阵中每一个算子都代表一个积分运算符,例如k域中有如下积分形式(忽略ω) &G"�r>,H�U [If��hh��2
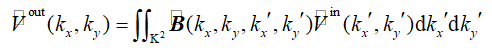 (3) f!"Y"g:@E� 其中K2代表输入组件的一系列k值, V为场分量的位置标识符, B表示公式2中一个矩阵元素的积分核函数。因为(kx,ky)代表k域中传输的平面波的方向,在K2的子集中核函数 (3) f!"Y"g:@E� 其中K2代表输入组件的一系列k值, V为场分量的位置标识符, B表示公式2中一个矩阵元素的积分核函数。因为(kx,ky)代表k域中传输的平面波的方向,在K2的子集中核函数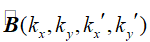 也可以被理解成方向角度的函数,说明了B是电磁场的双向散射分配函数(BSDF)的概括,尽管BSDF仅仅阐述了场能量效应。 �Y4�B<�]C4 -=A W. Z�o tt�K`*N��g 也可以被理解成方向角度的函数,说明了B是电磁场的双向散射分配函数(BSDF)的概括,尽管BSDF仅仅阐述了场能量效应。 �Y4�B<�]C4 -=A W. Z�o tt�K`*N��g 图2 上图展示了正弦表面光栅中的场,通过有限元方法(FEM)计算。此外,也使用了局部平面近似(LPIA)方法计算。在下图中展示了两种方法的结果,平面中结果场的振幅标为红色。由Rui Shi提供。 r\-25F�<e5
这必然被包含在了公式3中。因为BSDF的关系,我们选择 作为双向算子或者简化B算子。总的来说,计算B(k,k')和它在公式3中积分计算的应用需要大量的数值计算而且很慢。但是,在分层介质情况下,我们可以得到简化的形式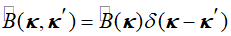 ,减少了乘积的积分,并且能够快速计算k域中的算子[4]。如果我们考虑Hirchhoff边界条件下的孔径效应,空间域中算子B则变成简单的因子形式,继而我们可以在x域中通过选择合适的傅里叶变化来模拟这个效应,这在图1中通过第一个B算子解释了。当然光学的主要任务是研究电磁场传播通过两种介质间的一般表面,例如透镜模型。 5@{+V!o,�� �l�6�S6�Y ,减少了乘积的积分,并且能够快速计算k域中的算子[4]。如果我们考虑Hirchhoff边界条件下的孔径效应,空间域中算子B则变成简单的因子形式,继而我们可以在x域中通过选择合适的傅里叶变化来模拟这个效应,这在图1中通过第一个B算子解释了。当然光学的主要任务是研究电磁场传播通过两种介质间的一般表面,例如透镜模型。 5@{+V!o,�� �l�6�S6�Y
3.几何算子 AIX�vS*Y�,
!dW77�kLTg 一般表面对场的影响可以通过有限元法(FEM)来计算,但是对于大多数情况来说,数值计算成本太高。如果表面的结构不是很小,在大多数实际情况中通过所谓的局部平面近似(LPIA)方法计算B算子可以得到足够的精度[5]。在这种近似中,电磁场的边界条件利用分层介质的已知解进行局部计算。图2比较了正弦表面光栅时FMM和LPIA的计算结果,结果显示LPIA对该效应预测的很好,即使是表面上非常小的特征。事实上,我们发现LPIA是计算公式3中B(k,k')包括矢量效应(公式2)的有力手段。需要注意的是,著名的薄元近似(TEA)方法是LPIA的简化特例。尽管LPIA可以计算双向算子,我们仍然需要进行公式3中大量的数值积分计算。这导致了LPIA和几何傅里叶变换的结合[3]。如果我们假设输入场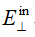 和输出场 和输出场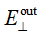 在它们的几何场域,它们遵循几何傅里叶变换理论 �Q$�(0�Nx< 在它们的几何场域,它们遵循几何傅里叶变换理论 �Q$�(0�Nx< 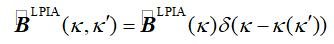 (4) Fc"��&lk4e 公式3中的积分再一次简化为简单的乘积,其中包括了坐标变换k(k')。根据几何傅里叶变换理论,这个变换由输入场的波阵面相位计算得到。我们将公式4中的算子称为几何算子。这个结果已经于VirtualLab Fusion中实现。如果场处于其几何或衍射区域,则可以在任何平面进行数值测试。根据结果,应用了不同的傅里叶变换,也以不同的方式应用了B算子。这造成了基于纯数学论证的衍射和几何模型自然而然地应用。建模始终完全基于物理光学并在数值效率方面进行了优化。 v�8`)h<:W? "n�3i�(sZ 参考文献 ;�I+�"MY7D [1] M. Kuhn, F. Wyrowski, and C. Hellmann, in vol. 66 of Lecture Notes in Applied and Computational Mechanics, pp. 257 (Springer Berlin Heidelberg, 2013) Sp]i~#�q_' [2] S. Zhang, D. Asoubar, C. Hellmann, and F. Wyrowski, Appl. Opt. 55(3), 529 (2016). o,s�w�[��� [3] F. Wyrowski and C. Hellmann, Proc. DGao, vol. 118, A37 (2017). s;0�eD5b>x [4] S. Zhang, C. Hellmann, and F. Wyrowski, Appl. Opt. 56(15), 4566 (2017). g}�-�Ch�#� [5] A. Pfeil, F. Wyrowski, A. Drauschke, and H. Aagedal, Appl. Opt. 39(19), 3304(2000). $.z~bmH"D� [6] Fast physical optics software “Wyrowski VirtualLab Fusion”, developed by Wyrowski Photonics UG, distributed by LightTrans GmbH, Jena, Germany. ab=�s+�[r1 �;|�hEXd?b (4) Fc"��&lk4e 公式3中的积分再一次简化为简单的乘积,其中包括了坐标变换k(k')。根据几何傅里叶变换理论,这个变换由输入场的波阵面相位计算得到。我们将公式4中的算子称为几何算子。这个结果已经于VirtualLab Fusion中实现。如果场处于其几何或衍射区域,则可以在任何平面进行数值测试。根据结果,应用了不同的傅里叶变换,也以不同的方式应用了B算子。这造成了基于纯数学论证的衍射和几何模型自然而然地应用。建模始终完全基于物理光学并在数值效率方面进行了优化。 v�8`)h<:W? "n�3i�(sZ 参考文献 ;�I+�"MY7D [1] M. Kuhn, F. Wyrowski, and C. Hellmann, in vol. 66 of Lecture Notes in Applied and Computational Mechanics, pp. 257 (Springer Berlin Heidelberg, 2013) Sp]i~#�q_' [2] S. Zhang, D. Asoubar, C. Hellmann, and F. Wyrowski, Appl. Opt. 55(3), 529 (2016). o,s�w�[��� [3] F. Wyrowski and C. Hellmann, Proc. DGao, vol. 118, A37 (2017). s;0�eD5b>x [4] S. Zhang, C. Hellmann, and F. Wyrowski, Appl. Opt. 56(15), 4566 (2017). g}�-�Ch�#� [5] A. Pfeil, F. Wyrowski, A. Drauschke, and H. Aagedal, Appl. Opt. 39(19), 3304(2000). $.z~bmH"D� [6] Fast physical optics software “Wyrowski VirtualLab Fusion”, developed by Wyrowski Photonics UG, distributed by LightTrans GmbH, Jena, Germany. ab=�s+�[r1 �;|�hEXd?b
5��w#*JK�� QQ:2987619807 ;�^,2
Qs�M
|