我们用偏振来描述光波电场的方向。虽然是很复杂,但它的影响是完全明确和可计算的。图1显示了一个简单的长波通滤波器在斜入射时的计算性能,其曲线标记为p-偏振、s-偏振和平均极化。这些名称是什么意思? nar=\cs~�g
c L84�}1QD f ��*)t<1f 图1. 在45°条件下计算的600nm长波通滤光片,显示了P偏振、S偏振和平均偏振的透射率。
&0N�d9%�> 让我们将讨论局限于完全各向同性的材料。所涉及的过程是线性的,允许我们将任何问题分解为一系列可以单独遵循的简单分量。对于Essential Macleod中的所有计算,基本分量是线偏振平面波(或单色光)。 ab
2�V�.S�
�h~<#1'/�< 当我们讨论偏振时,我们经常提到线偏振或平面偏振、圆偏振和椭圆偏振。在计算中,所有这些偏振被表示为两个正交线偏振的组合,其可以单独计算并且在透射或反射中的取向不变。它们有时被称为偏振的本征模式,这在斜入射时尤为重要。光学薄膜的作用是改变每种组分的振幅和相位。膜层的性能量化了这些变化。 �{%~Sbcq4F
*mBn''a"*� 如果没有参考系,那么这些性能参数是没有意义的,我们需要定义基准轴,电场的正方向,以及我们比较相位的点。Z轴垂直于膜层表面,其正方向与入射方向一致。X轴沿着膜层表面,与Z轴一起定义入射面。原点是Z轴与前表面面或入射面的交点。我们通常将入射面可视化为显示系统的平面,Y轴垂直于显示器,并向外指向观察者。 3`��-[�95w
�pW�!���]� 在垂直入射时,对线性偏振方向影响,因此我们将入射波中的电场的正方向设置为沿着正y轴。相同的惯例适用于反射波和透射波。对于相位参考点,我们选择入射波和反射波的坐标原点,但是z轴从发射波的后表面或出射表面出现的点,我们选择时间变量,使入射波的相位在参考点处为零。然后,反射和透射波的相位也就是反射和透射的相位变化。图2显示了这种约定。 t+66kB��N
�{K:�/�(�\ 我们约定中的不连续性会造成很大的困难,因此我们确保斜入射约定与正常入射约定兼容。我们需要一个s和p偏振的约定,因此选择电场的正方向,如图3所示。很明显,这一惯例在正常情况下崩溃,如图2所示。 _{T�`�k�a� "�%0R��R?� 图2. 电矢量正方向的垂直入射惯例。这适用于所有可能的线偏振方向。
6:QJ@�j�\ 图3. p和s偏振的电矢量正方向的惯例。
W>s<�&�Vb� 反射率R和透射率T是计算的重要参数,我们必须小心它们在斜入射时的定义。所涉及的光是无限大的平面波,它们超出了我们的接收器。在没有吸收的情况下,我们希望R和T相加等于一个单位(或100%),但是由于折射以及接收器位置的原因,这将无法实现。因此,我们在计算中使用辐照度的垂直分量。当光束直径小于接收器的光束直径时,该定义与使用受限光束(例如来自激光器的光束)的测量完全一致。 ~|?2<g$gYR
DfqXw^�BKD 除了反射率和透射率外,其他基本参数是参考点处反射波和透射波相对于入射波相位的变化。 SkN^�yt�KE
-Xx,"[sN\w Paul Drude在19世纪末发明了椭圆偏振光谱法,作为测量金属光学常数的技术。测量椭圆偏振的形状仅涉及相对测量,避免了绝对测量的巨大困难。定义椭圆需要两个量,它们可以采用不同的形式。 椭圆度和方向角是两个这样的量,但最常见的是沿两个定义的参考轴测量的振幅的比率及其相对相位。 不幸的是,振幅比可以从零到无穷大变化,这是一个困难的范围,更合适的数量是它的反正切。 如果参考方向是x,y和z,则z是沿着传播方向,当我们定义两个角度量时,ψ(psi)和Δ(delta)为 �yKq;E�cVx
];o�ED�?I� 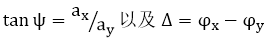 I7]4�5��pF
I7]4�5��pF
im*X�S@U�j 当我们观察镜子中物体的反射时,我们看到的图像与物体不完全相同,通常我们将其视为左右交换。无论我们解释它的哪种方式,右手系统的轴都变为左手,这也适用于我们的椭圆偏振参数突然的左手反射。通常采用的一种解决方案是反转反射中p偏振的正方向,但不是薄膜计算的良好解决方案。 为了保持一致性,我们应该在垂直入射时反转反射的p方向,但是如果没有入射平面我们怎么能这样做呢? 我们选择更简单的解决方案。 保留我们对p和s方向的定义,我们在反射中定义椭圆参数,但不在透射中定义 �k98-�-kc5
d6~wJ�M�Fl 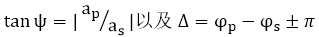 �>YPfk=0f0
�>YPfk=0f0
oSE'-���8( 对于非偏振光,在p方向和s方向之间没有相位关系,但是在倾斜入射时将存在偏振效应。如果接收器对偏振不敏感,那么该测量将对应于p和s偏振的平均值。由于两种模式的性能通常不同,因此将存在有效的ψ,并且也可以计算。 >i�aZGX�je
&XN*T�.�Y` 斜入射对偏振的敏感度在光学系统中可能会出现一些困难的问题。Polarization Maintenance(PM)是我们用来量化分量或系统保持偏振功能的术语,如图4所示。与入射面成45°角的线偏振光,由一个完善的系统反射或透射,输出时将保持不变。ψ将保持在45°和Δ在0°或180°之间,取决于奇偶校验。我们通过测量所需方向的输出辐照度和任何正交偏振光的输出辐照度来检查这一点,并将PM定义为所需偏振模式的辐照度与总辐照度之比,其比例为0至100.0%。PM是一个可优化的量。 � #]���n[ m|e�!1_�:H 图4. 115nm SiO2保护膜银反射镜在45°入射时的反射和反射PM。
�]+,Z���() 可以在堆栈文档或包含介质的设计中进行锥角光源入射计算。在这里,我们相对于入射光的轴向光线及其入射平面定义p和s偏振。无论偏振是什么,接收器都测量总辐照度。锥角光线中的偏斜光线具有局部入射平面,并且它们的p和s方向可以与轴向光线不同,从而导致锥体的偏振模式之间的泄漏。如图5 R?^FO:nM%! >uxak2nM-� 图5. 由准直光和5°锥角照射的31层立方体偏振器。
~�H?�RHYP~ Essential Macleod中有一些规定包括双折射层材料。它们的主方向的取向必须与参考轴一致。 �`5�h�$@�� QQ:939912426 0]NjsO�U�=