# M3d = q/@r# 简介 ] ONmWo77o [{`&a#Q 天文光干涉仪能够实现恒星和星系的高角分辨率的测量。首次搭建的天文光干涉仪分别由菲索（1868）和迈克尔逊（1890）提出。迈克尔逊恒星干涉仪于1920年成功地测出参宿四的直径。现如今，恒星干涉仪可用于前沿研究，如外行星识别和恒星的超高分辨率（4豪弧秒）
成像。在本文中，一种经典的迈克逊恒星干涉仪将会在FRED里面进行设计和分析。
G2> s#Y5(, _]3#C[1L 恒星干涉仪设计 =&.9z 4A A~0yMww:$ 系统的几何结构如图1所示。干涉仪由四个反射镜、一对小孔、一个正
透镜和一个探测仪组成。
fL'Ci;.;+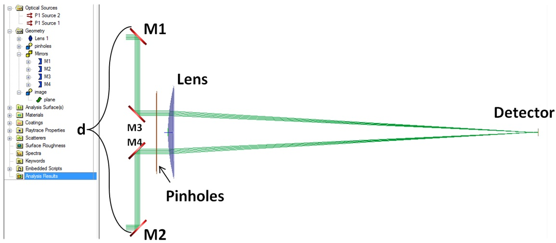 
awQB0ow'$P 图1 迈克尔逊恒星干涉仪的几何结构。反射镜M1和M2由可变的距离d分开。另一组反射镜使
光线转向通过不透明掩膜上的一对小孔上。一个平凸透镜放置在掩膜的后面，相应的具有吸收的探测器平面放置在透镜的焦平面处。
L1@<7?@X !{g>g%2! 考虑恒星的测量。恒星由一个多色光
光源模拟，它在一个小的角度范围内照射干涉仪，这对应于它的角直径。正常入射在两个路径P1和P2之间没有光程差。然而，进入到干涉仪中光线的光程差会随着角度的增大而增大。探测器上生成的干涉图样的一些例子如图2所示。
-B 7X;{
)7E7K%:b, 图2 左：角度范围为1弧秒的恒星在探测器上的白光干涉图样，白光的中心
波长为0.55um，半带宽为0.1um。干涉仪的小孔半径为1mm，反射镜距离为50mm。右：增加反射镜间距到100mm的干涉图样，此干涉图的能见度降低了。
E( *CEW.V* 1^WkW\9kO 全局变量的脚本 n5fc_N/8O= )U}`x }:, 条纹可见度是光源角度范围、
光谱含量、小孔半径和两个外反射镜（M1和M2）之间的距离d的函数。在实际中，改变反射镜间距可以获得预期的未知值：光源的角度范围。为了观察干涉图样上这些变量每个的影响，使用FRED内置的BASIC脚本环境，可以写入带有全局变量的嵌入式脚本。这些变量如图3所示。全局变量允许用户对脚本化FRED模型进行调整，而不需要直接编辑脚本本身。
NVf_#p "h 图3 迈克尔逊恒星干涉仪的全局脚本变量
CX5>/ J RtDjZ4> 嵌入式脚本可以用于产生具有合适波长和角距的光源，来代表恒星对象。实现这个目的的一种方法是产生一对相干的平面波光源：一个光源就位于M1之前，另一个就位于M2之前。每个光源都有基于光源光谱的合适的波长和相对功率，并且在提供的角度直径内的任意方向传播。一旦所有的光源创建好，相干光线追迹就会执行。在探测器平面上的辐照度和彩色图会得到计算并显示出来。为了模拟迈克尔逊恒星干涉仪的运行，额外的循环可以添加到脚本中，它会在每一步扫描反射镜间距并计算条纹可见度。条纹可见度的第一个极小值会出现在d=λ0/(2θ)处，其中λ0是恒星（发光）的中心波长，θ是以度为单位的角距。
iWe'|Br DsHm,dZ [1] “Astromomical Interferometer.” Wikipedia. September 16, 2015. Accessed December 15, 2015.
https://en.wikipedia.org/wiki/Astronomical_interferometer oHu 7<r u+pZ<Bb [2] “Michelson Stellar Interferometer.” Wikipedia. June 15, 2014. Accessed December 15, 2015.
https://en.wikipedia.org/wiki/Michelson_stellar_interferometer. `w "ooK h?- >A# [3] “Measurement of Stellar Diameters.” Brown, R. H. Annual Review of Astronomy and Astrophysics, vol. 6, p.13. 1968
)fke;Y0 PL3oV<\4s> 玻片 Q$yQ ^ mG eF Qz G+/ Vg"v C 简介
}[;r-5} h{ EnS5~ FRED具备通过
光学系统模拟光线偏振的能力。光源可以是随机偏振、圆偏振或线偏振。过滤或控制偏振的光学元件，如双折射波片和偏振片，可以准确的模拟。FRED偏振模型中一些简单例子包括吸收二向色性和线栅偏振片，方解石半波片，和马耳他十字现象。这些特性的每一个都可以应用到更复杂的
光学系统中，如液晶显示（LCDs）、干涉仪和偏光显微镜。
axkNy}ct 'f7s*V KG 波片模型 i)]^b{5nyB Pi Nf;b^9 波片是由寻常光和非寻常光具有不同折射率值的材料制成。取向合适时，波片可以改变光线的一个偏振分量（相对于另一个），从而改变它的偏振态。四分之一波片使线偏振变成圆偏振，反之亦然。半波片使x偏振光变成y偏振光，或者右旋偏振光变成左旋偏振光。
_G^ 4KwYp 7VfPS5 se 从FRED系统的X偏振片示例开始，波片元件添加到了x偏振片后面（图1）。模拟一个波片有两种方法。最简单的方法是指定一个1/2波片涂层到一个表面上。在FRED文件的Coatings分类下，用户可以右键点击Create a New Coating….在下拉菜单中，可以选择“Polarizer/Waveplate Coating (Jones matrix)”。对于这个例子，涂层类型选择“1/2 wave +45 Fast Axis”。这样可以保证波片的晶轴相对于x偏振的入射光旋转45度。
图1 随机偏振光通过x偏振片过滤。剩余的光线通过一个+45°1/2波片（黄色），它可以将x偏振光转换成y偏振光。
R\u5!M$:: 92/_!P>
模拟波片的一个更加精确的方法是指定一个自定义双折射材料到一个杆状元件中。在FRED文件的Material分类中，用户可以右键点击并选择Create a New Material….在下拉菜单中，可以选择“Sampled Birefringent and/or Optically Active Material”。对于这个例子，晶轴偏转+45°（0.707,0.707,0），然后定义下面的材料特性（基于方解石晶体）：波长=0.59um，no=1.658，ne=1.486，ko=0，ke=0。
g JOD+~ % )}rQqQ 作为1/2波片，一定要选择杆的长度，这样寻常和非寻常偏振分量可以通过1/2λ的净值分隔开来。
94[8~_{fG msZ 3%L 其中L=杆长，λ是以系统单位表示的光波长，K是一个整数，no和ne是双折射率的寻常和非寻常分量。通过这个块状双折射材料的光线追迹会将每个光线分成寻常和非寻常分量。作为分析结果，偏振点图（Polarization Spot Diagram）将会显示每个单独的分量（图2）。
t8 ~isuiK 图2 x偏振光通过一个方解石1/2波片后的偏振点图。偏振的寻常和非寻常分量绘制成单独的光线。
*adwCiB DC'L-]#< 为了保证光线确实是y偏振的，在探测器表面显示了相干矢量波场（Coherent Vector Wave Field）。选择右键菜单“Show X Component of Field”，然后再次点击右键，选择“Show Statistics”，可以观察到x偏振分量上能量的积分。比较X分量和Y分量，可以证实几乎所有的入射能量都在y偏振分量上。
7<93n`byM -&LF`V&3w 波片的厚度决定了到达探测器x和y偏振光的比值。为了说明这一点，使用3°楔形方解石替代杆状波片。相干场的x和y分量如图3所示。
6 J3<k (#: 图3 x偏振光通过具有+45°光轴的楔形方解石晶体后，探测器上相干矢量场的x和y分量。波片厚度沿着y方向变化，因此在沿着楔形周期性位置处担当着1/2波片的角色。
