概述 j�(��k%w�
CAx�
eJ`Q 1928年,光波被散射后频率发生变化的现象被印度物理学家拉曼发现,因此被命名为拉曼散射。拉曼散射可以分为自发拉曼散射和受激拉曼散射。自发拉曼散射源于热振动声子对于入射光的散射。受激拉曼散射则是强激光与物质相互作用时产生的受激声子对于入射光的散射。 ���AEx VKy -{C Gn5]_# 系统描述 �t_16icF9U
h�{zb�)�'R 本例展示了如何模拟瞬态拉曼效应。当高功率超短激光脉冲在大气中传播时,若脉冲宽远远小于拉曼过程的时间常数,则该作用过程就可以通过求解描述瞬态拉曼过程的方程组进行模拟。理论手册第9章中包含对瞬态拉曼效应方程的完整描述。 T.')XKP)1N
ai?�N!RX%H 在瞬态拉曼效应的模拟过程中有一个关键问题需要解决,那就是如何处理自发辐射的角度。更精细的空间采样就可以考虑更大的立体角。在本例中,我们只考虑初始10ps的作用过程,这样瞬态增益将会比稳态增益小很多。模拟过程中我们将传播距离分30步完成,每一步1km,每一步综合考虑自发拉曼效应、受激拉曼效应以及衍射效应。 oa=TlB��k<
Z5F#r>>�` 没有受激拉曼放大下的自发辐射开始会线性增长,但是随着传播距离的增加,就会有越来越多的空间分量散射出主光路,最终自发辐射到达一个稳定值。越大的采样阵列能够涵盖的自发辐射角度越大,但同时散射效应作用的距离也更短。 ��\
q��q�� ���E�bX!;z
模拟结果 NX8hFw���R Qv'x+GVW] 图1.没有受激拉曼放大下时自发辐射的增长过程(采样阵列为64*64)
8D�@���J�d 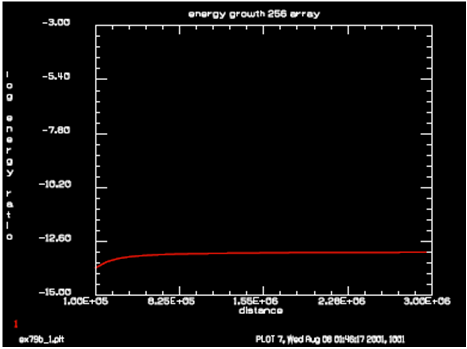
图2.没有受激拉曼放大下时自发辐射的增长过程(采样阵列为256*256)
图3.30km处斯托克斯光的分布(采样阵列为64*64)
图4.30km处斯托克斯光的分布(采样阵列为256*256)
图5.斯托克斯光与入射激光的强度比随传输距离的变化(对数坐标,采样阵列为64*64)
图6.斯托克斯光与入射激光的强度比随传输距离的变化(对数坐标,采样阵列为256*256)