j3rBEQ,R 简介
A:EF#2) g Nf>1 `e P 天文光干涉仪能够实现恒星和星系的高角分辨率的测量。首次搭建的天文光干涉仪分别由菲索（1868）和迈克尔逊（1890）提出。迈克尔逊恒星干涉仪于1920年成功地测出参宿四的直径。现如今，恒星干涉仪可用于前沿研究，如外行星识别和恒星的超高分辨率（4豪弧秒）
成像。在本文中，一种经典的迈克逊恒星干涉仪将会在FRED里面进行设计和分析。
E {d Mdz l'(C xhf.W 恒星干涉仪设计
;5A&[]@^^@ 2i4FIS|z0 系统的几何
结构如图1所示。干涉仪由四个反射镜、一对小孔、一个正
透镜和一个探测仪组成。
uRQm.8b %lchz /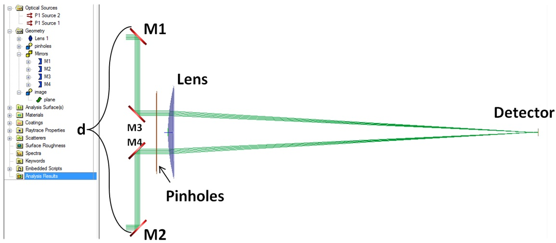 
d^IOB|6Q 图1 迈克尔逊恒星干涉仪的几何结构。反射镜M1和M2由可变的距离d分开。另一组反射镜使
光线转向通过不透明掩膜上的一对小孔上。一个平凸透镜放置在掩膜的后面，相应的具有吸收的
探测器平面放置在透镜的焦平面处。
o*\kg+8 sD .bBz 考虑恒星的测量。恒星由一个多色光
光源模拟，它在一个小的角度范围内照射干涉仪，这对应于它的角直径。正常入射在两个路径P1和P2之间没有光程差。然而，进入到干涉仪中光线的光程差会随着角度的增大而增大。探测器上生成的干涉图样的一些例子如图2所示。
Ay!=Yk ^~ vt[4"eU 图2 左：角度范围为1弧秒的恒星在探测器上的白光干涉图样，白光的中心
波长为0.55um，半带宽为0.1um。干涉仪的小孔半径为1mm，反射镜距离为50mm。右：增加反射镜间距到100mm的干涉图样，此干涉图的能见度降低了。
vfJ}t#%UH TdP_L/>|J 全局变量的脚本
UnZ*"% Va06(Cq 条纹可见度是光源角度范围、
光谱含量、小孔半径和两个外反射镜（M1和M2）之间的距离d的函数。在实际中，改变反射镜间距可以获得预期的未知值：光源的角度范围。为了观察干涉图样上这些变量每个的影响，使用FRED内置的BASIC脚本环境，可以写入带有全局变量的嵌入式脚本。这些变量如图3所示。全局变量允许用户对脚本化FRED模型进行调整，而不需要直接编辑脚本本身。
I~MBR2$9 V# |#%
8 图3 迈克尔逊恒星干涉仪的全局脚本变量
K Gkz E 嵌入式脚本可以用于产生具有合适波长和角距的光源，来代表恒星对象。实现这个目的的一种方法是产生一对相干的平面波光源：一个光源就位于M1之前，另一个就位于M2之前。每个光源都有基于光源光谱的合适的波长和相对功率，并且在提供的角度直径内的任意方向传播。一旦所有的光源创建好，相干光线追迹就会执行。在探测器平面上的辐照度和彩色图会得到计算并显示出来。为了模拟迈克尔逊恒星干涉仪的运行，额外的循环可以添加到脚本中，它会在每一步扫描反射镜间距并计算条纹可见度。条纹可见度的第一个极小值会出现在d=λ0/(2θ)处，其中λ0是恒星（发光）的中心波长，θ是以度为单位的角距。
f
5_n2 mUzNrkG(G [1] “Astromomical Interferometer.” Wikipedia. September 16, 2015. Accessed December 15, 2015.
BG"~yyKA B N@*CG [2] “Michelson Stellar Interferometer.” Wikipedia. June 15, 2014. Accessed December 15, 2015.
>\8Bu#&s4 i)\`"&.j>N [3] “Measurement of Stellar Diameters.” Brown, R. H. Annual Review of Astronomy and Astrophysics, vol. 6, p.13. 1968
