x&l?Cfvv�= 本
教程示例遵循P. Lalanne等人[1]研究的基准问题设置[2]。同时演示了相同设置下的FEM性能。基准问题包括计算由平面波入射的孤立(即非周期)模式中的近场。该几何
结构由基板上银膜中的孤立亚
波长狭缝和银膜中相邻的平行凹槽组成。平面波垂直入射该装置,并具有平面内电场极化(分别为面外磁场极化)。通过狭缝传输到位于狭缝下方特定距离的
探测器区域的光的能量通量被检测,并归一化为通过狭缝的能量通量,在不存在凹槽的第二次
模拟中计算。由于几何、
光源和
材料的特性,等离子体效应导致了归一化透射对物理
参数的非常关键的依赖。这使得
标准化传输的准确计算成为具有挑战性的基准问题。
nO�kX:��5 狭缝槽设置(左)和用于归一化的狭缝设置(右)的三角形网格;灰色:银膜,蓝色:基板,红色:检测器区域,绿色:空气;请注意金属角处网格的预细化。
�)�3.��udx 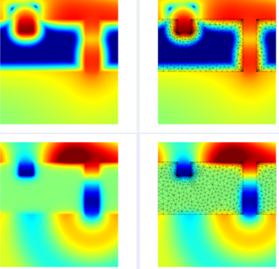
计算后场强度,有有限元网格部分(右)和没有限元网格部分(左)(顶行: 图 ,底行: 图 ,伪色标)。 U�m�v�_{n`
��Wv�77e�f data_analysis文件夹还包含一个脚本,用于执行有槽和没有槽的模拟(根据基准问题,用于对能量流进行规范化)。该脚本还允许更改数值和物理项目参数,例如,检查准确性。下面显示了一些示例字段分布。
K�^J;iu��4 N� ]}Re$�5 [1]P. Lalanne, et al., Numerical analysis of a slit-groove diffraction problem, JEOS - Rapid 2, 07022 (2007).
BN��y�DEFd [2]S. Burger, et al., Finite-element based electromagnetic field simulations: Benchmark results for isolated structures, Proc. SPIE 8880, 88801Z (2013),
http://arxiv.org/pdf/1310.2732