Yg<L pjq5X 本文讨论了如何使用FRED对球
透镜封装的
半导体激光二极管耦合到单模
光纤进行准确的建模,这是在光纤通信领域很常见的一个
光学系统。该模型演示了FRED传播相干光场的能力、它的精确激光二极管束(Laser Diode Beam)
光源模型以及准确的计算光纤耦合效率。
i�]cD{��hv B5A/Iv�)�2 模型 ;c�/|L�Xc\ >P<�8E2�}* 在FRED模型中使用的半导体激光二极管是Mitsubishi(三菱) ML725C8F,这是一个InGaAsP / InP多
量子阱(MQW)
激光器,工作波长是1310nm。Mitsubishi光源说明书定义了输出光束的在x和y方向的发散角分别是25和30度(远场功率分布的全1/e宽度)。没有提及在x和y焦点位置的任何偏移,所以我们假定它们和光源处的分布是一致的。
h]�+UK14�m ^cz4��nW<� 我们在FRED中使用激光二极管束光源类型对激光二极管光源建模,以及设置光源产生相干输出。
`i�2:@?Kl9 图1. 激光二极管光源编辑
�Y:�?c�WO H1t`�fyri2 注意到在激光二极管光束光源的设置里面,发散角由功率的1/e2标准定义。这就要求制造商提供的发散角要乘以一个开方因子。
8m�m]�>u�$ 图2. 球透镜封装的激光二极管耦合到光纤系统原理图(侧视图)
#NyfE|MKBC 直径为1.5mm的球透镜是Mitsubishi激光二极管集成的一部分,它的位置在距离激光二极管发射表面1.88mm处。
**G5f�S.^W M1�mx�{<]A 在FRED中使用球形元件基元,就可以创建该透镜。为方便起见,全局坐标原点选在球透镜的输出表面与光轴的交点处。
�O�G��R2Y 图3. 全局坐标原点的定义
�b�o-A��M] �/�g`!Zn8a 值得注意的是,我们使用了FRED的N-BK7模型来定义球透镜的材料,在1310nm波长处折射率大小是1.5036。
WR�.>?IG2E cb�3Q{.-.# 模型中使用的单模光纤(SMF)位于距离全局坐标原点1.9mm处,它的结构(由下图定义)基于单模光纤的典型值。光纤纤心的半径是5μm,且由直径为125μm包层包裹着。纤心和包层的折射率大小分别是1.465和1.47,它们之间的折射率差为0.36%。
GX��nrVI� 图4. 单模光纤示意图
�ez-jVi-Fi �3
0.&Lzz� 模型中还包含了一个吸收涂敷层,或者是夹层,覆盖在光纤表面。
0�X�<U.Sxn G`e!Wv��C� 在FRED中定义的光纤是一个组件,它包含了多个元件基元:一个圆柱体用于纤芯、光管用于包层和涂敷层。
<G_71J`MLC /'l"Us},^! 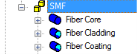 N�d ��h� �#i�iXJnG�
N�d ��h� �#i�iXJnG� 注意到“Fiber Cladding”管道的内壁恰好与“Fiber Core”圆柱体的外壁是重合的。为了正确的建模,用户需要手动的设置包层管道的内壁为不可追迹(Never Traceable)。不这样做的话将会导致光线追迹错误,因为两个表面放置在空间里完全一样的位置,而且它们具有两个不同的材料设置。对于“Fiber Coating”的内壁需要同样的设置。
"!B\�c9�q� Ylhy�Z�&a, 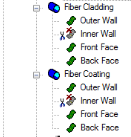 rj���
] ~g �!jTxMf�
rj���
] ~g �!jTxMf�
在这一模型中光纤涂层认为是吸收的,且拥有停止所有(Halt All)光线追迹控制。所有其它的表面是不加涂层的。
�`9Rj;^N�J t?(fDWd|�- 仿真 !{+a�2�w�i 5�-RA�<d#� FRED使用如下的方程来计算光纤耦合效率(CE):
=T-�jG_.H� �r
[�E4/?_ 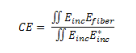 1KadT7<0}� S]Q�f
p�,�
1KadT7<0}� S]Q�f
p�,� 其中Einc是入射场分布,Efiber是光纤基模的场分布(由FRED根据光纤规格
参数自动计算)。
ri1;��i= W ]~@��uStHn 一般来说,CE是一个复数,所以耦合功率实际上是:
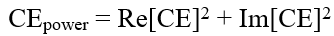 �u_�=^Bd�� V��vUP;o&/
�u_�=^Bd�� V��vUP;o&/ 因此,我们要想精确的计算光纤耦合,需要在光纤入口的后面放置一个分析面来保证该表面的反射系数能够准确的纳入考虑之中。
_B?Hw[cc
pt%*Y.)a�z 非常重要的是,分析面是大于我们所期望的基模的模场直径(MFD),以便进行精确的重叠积分。同样重要的是,我们应该意识到数值积分的精确性依赖于分析面中划分网格的数目。在本例中,50μm宽的分析面上251×251的网格,可认为是足够的。
m7|S'{�+�! 图5. 分析面放置在光纤界面的后面
@b9qBJfQ�� 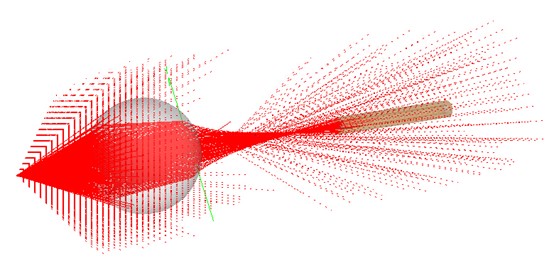
图6. 光源用128*128采样点光线追迹与渲染
AN�RZQpnXQ d�Ar�=X4LE 由FRED光纤耦合效率计算得出的返回值是两个场分布之间的重叠部分,且没有考虑入射场的功率。因此要想知道多少功率耦合到该模式中一定要做到以下两步:
H�1d�2WNr[ 5|A"Yz��Y# 1.通过辐射照度的计算确定分析面处的功率值(P)
XE$;Z'Qhjm lyzM?lK�- 2.通过光纤耦合效率分析确定CE的值
+&4@H�HU{G rM`z2*7%�d 耦合到光纤模式中的功率大小可以简单的表示为P * CEpower。
2@Zw�#2|�] RD�OV+�2�K 追迹完从具有2048×2048个样本点的光源发出的光线后,当我们计算辐射照度时,输出窗口里就会显示出到达光纤接口后面的分析面处的光源功率值。
~�[�Z�(6yX 图7. 分析面处的积分功率值
hiE�o�sI
C �n+1�`y8dy 可以看出,26.55%的光功率到达了分析面。为了确定到光纤模式中的耦合,这里使用了FRED光纤耦合效率分析。注意到0.005mm的光纤纤芯半径在这里需要准确的输入。
v@�,`(\Ca' 图.8 光纤耦合效率分析对话框
�0O?�\0k;o E^B�3MyS^^ 点击完OK后,结果会显示在输出窗口中。
b=kY9!GN,v 图9. 光纤耦合效率显示在输出窗口
20w4
'@sq
T[- %�b9h> 可以看出,耦合效率为71.44%。因此,在这个系统总的耦合功率百分比为71.44%*26.55% = 19.0%。
D�n4�8?A[v �6t{G{ ]�� ML725C8F激光二极管工作光源是在5mW,因此在该配置中,光纤传输的信号差点不到1mW。
p+;;01Z+_� o0_�H(��j? 对齐灵敏度
G6bvV*�TRi }\QXPU{UVd 对于测定设计公差以及激光二极管/光纤包的可行性,理解光纤对齐灵敏度是非常有必要的。使用FRED脚本功能可以很容易的完成这件事。
6Z5$cR_vC7 sit�gz)Ki^ 与该FRED文件相关联的共有三个内置脚本:
d~KTUgH�'< 纵向距离扫描
RREl(�$$�p 横向偏移扫描
}Xb|Ur4�3� 倾斜扫描
w�1��9OOD R(s[�JH(�& 这三个脚本之间是相似的:通过用户控制的步长,每个脚本调整了光纤的位置、计算了耦合系数并打印到输出窗口或者到Microsoft Excel电子表格中(如果有需要)。
{8556>��\~ �Xd�h@ ^`� 纵向对齐灵敏度
��mGo���NT b�lUS6"kV} 在距离扫描脚本文本的顶端,用户输入光纤的开始和结束位置,以及希望运行的扫描分辨率(步长)。
F$S/zh$)�0 �nK`H;��k� 如果用户希望FRED将数据打印到Microsoft Excel电子表格中并绘图,就要设置exportToExcel标签值为True。
t!59upbN}3 d*$�x|B�|V 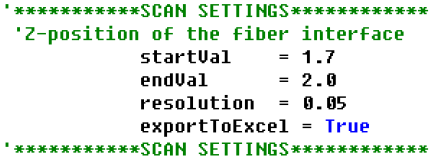 `_x#`%!#2� b_)SMAs�O7
`_x#`%!#2� b_)SMAs�O7 就在这定义了光纤的参数,这只是用于光纤耦合效率的计算。
I:W�PP'L4o �lN�M�Jcl3  0x�#
��V � Gh}* <X;N�
0x�#
��V � Gh}* <X;N� 头部打印出来后,脚本的主循环就开始了。这是一个“for”循环,它会一步一步的改变光纤的位置-[1],追迹光线-[2],计算照度并确定总功率-[3],计算光纤耦合效率-[4],最后计算模式功率-[5]。
G+t�zp&G@� 图10. 位置扫描脚本的主循环
�!1mAq+q!� iV�:\,<�8d 注意到函数FiberCoupleStepIndex返回了两个值-“coupleReal” 和“coupleImag”,这些变量是耦合系数的实部和虚部。
y\:,.cZ+TQ �.u�B[z�Jc 下图表示的是,对于球透镜到光纤的距离从1.5mm到2.5mm变化的结果。
�hVdGxT�]6 图11. 光纤耦合vs距离
RN$q,f[�#� Q6n8��,2�* 激光二极管的制造商Mitsubishi指定了在距球透镜1.9mm位置处,光纤耦合功率的最大值为0.8mW(16%的效率),FRED在耦合中计算出了稍微偏大的值。这种差异可以解释为:耦合对光纤模式尺寸和折射率分布极为敏感。很遗憾的是,Mitsubishi没有给出使用光纤的具体细节。
!i�AZEOkRR Pr,C)uc�h 横向准直灵敏度
�X*a7�`aL� (L!u[e0[#� “横向偏移扫描”脚本与之前十分相似,除了用户为扫描定义了如下的参数:
/U>��8vV+C �UMH�~�Q`" 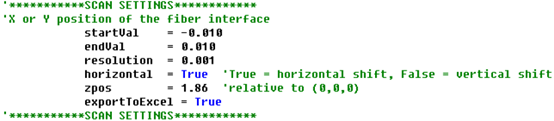
图12. 在Z=1.86mm位置处:光纤耦合vs横向偏移
�eGUe#(I / ��\}K�ad\) 方向灵敏度
m|[�cEZxHB r#d]"3tH�� 该脚本同样与先前的脚本十分相似,这里用户定义了取向的角度范围。注意到该脚本只是在水平方向倾斜了光纤,并不是一个任意的角度。
�<)�+;B��g 图13. 在Z=1.86mm位置处:光纤耦合vs水平方向旋转 {�"�0n^�!
OA7=k�H@3c 结束语 2|`~3B�)�# �sA�
}X)aP 在本文中,FRED展现出了从激光二极管到光纤耦合准确计算的能力。其计算结果与激光二极管生产商提供的耦合信息一致。FRED的相干传输能力以及高散射相干的精确定义对于这种类型问题的仿真是很关键的。
�(A;HB@)[A 6wb M$|yFj 本例系统数据(单位是mm)