-
UID:317649
-
- 注册时间2020-06-19
- 最后登录2025-04-09
- 在线时间1762小时
-
-
访问TA的空间加好友用道具

|
此示例演示了由不同电介质界定的银薄膜的等离子体激元波导的计算。 该设置遵循 Berini [1] 的举例。 我们主要评论整个计算域上电场强度的数值解,它代表了一个等离子体激元。 但是,对于传播模式项目,也会计算传播常数(传播模式)。 F
@uOX�Nz)
p&lT! 5P!A 几何示意图如下: Os[�50j!4>
VX'G\Zz@h|
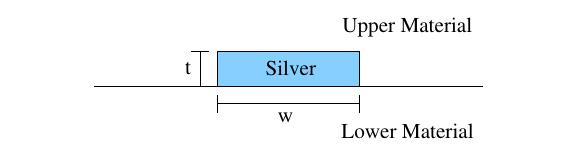 ��(BZd�%! e[��g.�&*! 下层和上层材料的相对介电常数由 ��(BZd�%! e[��g.�&*! 下层和上层材料的相对介电常数由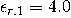 和 和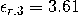 给出。这个金属薄膜的厚度是和宽度是 给出。这个金属薄膜的厚度是和宽度是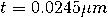 。分析了真空波长为 。分析了真空波长为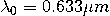 时的结构。金属薄膜(银)在该波长的相对介电常数为 时的结构。金属薄膜(银)在该波长的相对介电常数为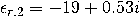 。 G8��@LH��� 。 G8��@LH���
0F�%�V+Y\R 在本例中,我们计算具有相对于波导对称平面的镜像对称电场的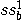 模式 [1]。 因此,只需离散化几何结构的一半就足够了。经过最后一步细化后的三角形几何部分如下图所示。 7,�2#0Z`ge 模式 [1]。 因此,只需离散化几何结构的一半就足够了。经过最后一步细化后的三角形几何部分如下图所示。 7,�2#0Z`ge
%5�Zhq��>� .t�zQ
�hd>  hOr�4�C4
hOr�4�C4
|