RED在高斯光线分解理论（GBD）的一个普遍形式下可以对形形色色物理光学现象做出合理的解释。在过去的25年间，经过改进的GBD算法，已经可以精确的模拟衍射和干涉现象，并且与事实忠实的吻合。这种完美的艺术是它在模拟用衍射仪观察泰伯效应和局部相干性上的应用的一个很好的例子。 g*nh8 GBD背后的基础是1969年被Arnaud首先提出的，他提出：一个任意波可以由一组高斯光线的基础组合而合成，而那些高斯光线可以用射线来追踪。普通的GBD方法在两种极端条件下限制了这种合成。当光线被放置在平行隙缝的光栅上，它会发生一种特殊的分解，或者在一种空间频谱含量的条件下发生傅里叶分解。后来Gabor延伸拓展了Arnaud的方法，FRED应用这种拓展使这两种方法结合成一种，以便更灵活的适应更宽范围的的条件。 ?onTW2c G; eJ3w}"?9s sAG#M\A6 @1UC9}> 泰伯效应 utDjN" 泰伯效应是由近场衍射产生的，在光线接近光栅或者其它周期性结构时可以观察到。在变化的衍射极之间产生的干涉使周期性结构沿着传播方向上在他们各自的泰伯距离处自
成像。
]a}K% D)H 即： L泰伯=
a×a 9+o`/lk1 λ 此处，a为光栅的间距，λ是
波长。
~j&#DG& L 泰伯效应在平板印刷术中也有应用，它被用来复制周期出现的微小结构。分时间隔的泰伯距离处会发生光栅频率的增倍。
YA vO V-L 假设一个直线光栅凹槽频率是100 lp/mm。光栅在FRED中以如图1所示的平面对话的光栅片定义。FRED可以在用户定义的衍射效率上对光线的分离产生多种的调整，并且分散这些调整中产生的能量。因为光线分离被FRED的射线痕迹追踪
系统控制，而被分配到分割面的追踪控制的反射组系水平中断应该被设置成与同衍射极的数量相等。
18xT2f 在这个例子中 ，光栅被设置成为一个1mm直径 0.5um波长的的准直栅格。当栅格间距为50um时，泰伯距离就为5mm。分析平面被用来计算1/2 泰伯距离处发光辐射的倍率，即图2给出的条纹。这里的计算包括光栅的0级
光谱条纹，正负一级光谱条纹，正负二级光谱条纹。交替峰高的变化和不同阶下的能量分布有关。
J XKqQxZ[X (`
N@4w= 衍射仪 TZ2-%k# 衍射仪在演示局部相干性上是一个非常有用的工具。它试验的设施放置如图3。非相干
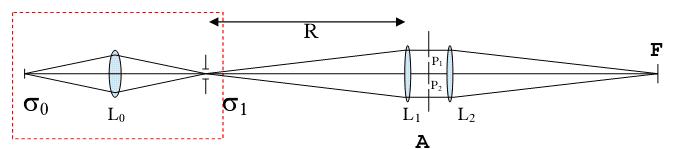
光源σ0被透射镜L0扩大后在σ1上小孔成像，光从σ1发射来后被透射镜L1转化为平行光，然后通过照射在透镜L2上重新在平面F上聚焦成像。一个上面有两条隙缝P1，P2的不透明屏幕A被置于L1和L2中间，且P1和P2的宽度，形状和位置可以被任意设定。
)@O80uOFh nYc8+5CcK' zFn-V EJ)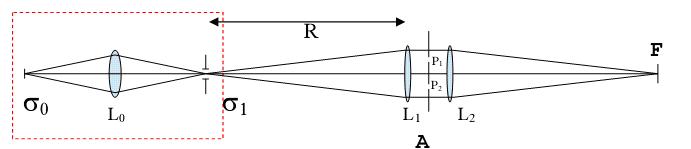 
9 J0JSy 图3 衍射仪（汤普森与沃尔夫）
E~y@ue: 在FRED的模式下，图3中红虚线范围内的部分被一个可以收集发射变化波长的任意阳极代替，位于一个面积与小孔σ1面积直径相同的区域内。这个发射源收集器的原理与Born & Wolf的准单色源的定义相符。在平面F上，每个波长都由单独产生由耦合生成的干涉图的发射源组成。有意的，FRED集合了不相干的相干波和不同波长。这样，显示在F上的辐照图就变为了相干组分的非相干组合。根据由P.H. van Cittert在1934年独立发表和之后的F. Zernike在1938年提出的一个重要的局部相干定理，采集源在σ1处引发了在屏幕A区域中P1和P2上任意两点的关联。范西泰特—策尼克定理定义了部分相干的复合度即：
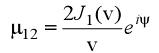
，其中
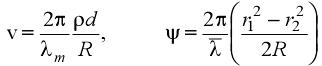
，ρ为小孔σ1的半径，d为P1和P2的中心距，R是L1的
透镜焦距，r1和r2分别为从光轴到P1，P2的距离，λm是平均波长。
XsVp7z k\ 为了测试FRED的性能，我们计算了平面F上的辐照图的缺口长d与P1，P2之间长度距离的变化，得到了与汤普森与沃尔夫相吻合的结果。测试时的
参数模型是f1=f2=R=1520mm；L1，L2之间的距离为14mm；小孔面积的直径为90um；光阑P1，P2的直径为1.4mm；平均波长λm为0.579um。FRED在高斯光线分解理论（GBD）的一个普遍形式下可以对几何光学现象做出合理的解释。在过去的25年间，经过改进的GBD算法，已经可以精确的模拟绕射和干涉现象，并且与事实吻合。这种完美的艺术性表现在模拟用绕射仪观察Talbot效应和局部同调性上的应用的一个很好的例子。
_4]GP3 ` GBD的基础是1969年被Arnaud首先提出的，他提出：一个任意波可以由一组高斯光线的基础组合而合成，而那些高斯光线可以用射线来追踪。普通的GBD方法在两种极端条件下限制了这种合成。首先当光线被放置在平行隙缝的光栅上，它会发生一种特殊的分解，或者在一种空间频率的条件下发生傅里叶分解。后来Gabor延伸拓展了Arnaud的方法，FRED应用这种拓展方法，使这两种方法结合成一种，以便灵活的适应各种范围的条件。
YFF\ m{# Talbot
效应 o'8`>rb Talbot效应是由近场绕射产生的，在光线接近光栅或者其它周期性结构时可以观察到。在变化的绕射极之间产生的干涉使周期性结构沿着传播方向上在他们各自的Talbot距离处自成像。 >8*J ;(:W +l " z 即：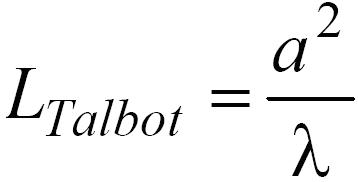
此处，a为光栅的间距，λ是波长。
X4"D Lt" Talbot效应在光微影技术中也有应用，它被用来复制周期出现的微小结构。分时间隔的Talbot距离处会发生光栅频率的增倍。
Gidh 7x m1mA:R\zM I}&`IUP 假设一个直线光栅凹槽频率是100 lp/mm。光栅在FRED中以如图1所示的平面对话的光栅片定义。FRED可以在用户定义的绕射效率上对光线的分离产生多种的变化，并且分散这些调整中产生的能量。因为光线分离被FRED的光线追迹系统控制，
而被分配到分割面的追迹控制的反射组系水平中断应该被设置成与同衍射极的数量相等。 f`dQ $Kh 在这个例子中 ，光栅被设置成为一个1mm直径 0.5um波长的准直同调光。当光栅间距为50um时，Talbot距离就为5mm。分析平面被用来计算1/2 Talbot距离处发光照度的倍率，即图2给出的条纹。这里的计算包括光栅的0级光谱条纹，正负一级光谱条纹，正负二级光谱条纹。交替峰高的变化和不同阶下的能量分布有关。
!G0OD$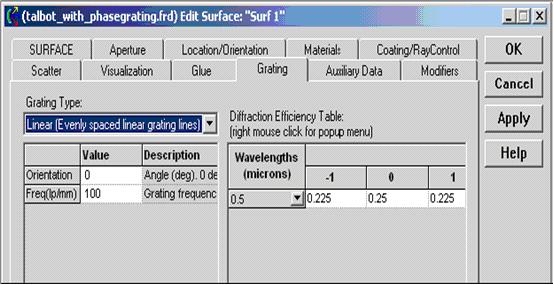 
z,"fr%*,N Figure 1. 光栅定义.
|NsrO8H
/R 2 K3E#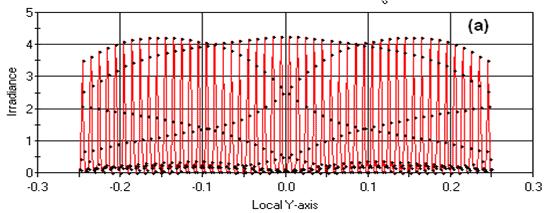 
y Jj$ir i 
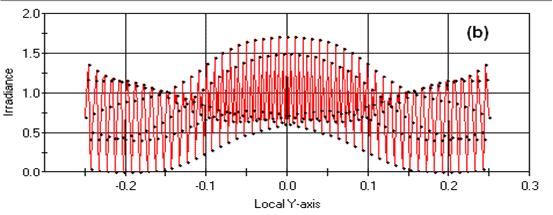h*2NFL~# z)Is:LhS Figure 2. 塔尔博特效率(Talbot Effect)干涉条纹计算于(a) LTalbot = 5mm且每0.1mm展现10 个峰值(b) 1.5* LTalbot = 7.5mm且每0.1mm展现20个峰值 (H\)BS7#R Diffractometer 绕射仪 {g%F 3- 绕设仪在演示局部同调性上是一个非常有用的工具。它试验的设施放置如图3。非相干光源σ0被透射镜L0扩大后在σ1上小孔成像，光从σ1发射来后被透射镜L1转化为平行光，然后通过照射在透镜L2上重新在平面F上聚焦成像。一个上面有两条隙缝P1，P2的不透明屏幕A被置于L1和L2中间，且P1和P2的宽度，形状和位置可以被任意设定。
1${lHVx]
图3 衍射仪(after B.J. Thompson and E Wolf)
^"g # ! =Qa*-* 在FRED的模式下，图3中红虚线范围内的部分被一个可以收集发射不同波长的任意点光源代替，位于一个面积与小孔σ1面积直径相同的区域内。这个发射源收集器的原理与Born & Wolf的准单色光源(quasi-monochromatic source)的定义相符。在平面F上，每个波长光源都产生独立相对应的干涉图形。FRED集合了同调及不同调的光源及不同波长设计。因此显示在F上的辐照图就变为了同调组合及非同调组合。根据由P.H. van Cittert在1934年及F. Zernike在1938年所各自独立发表重要的局部同调定理，采集点光源在σ1处引发了在屏幕A区域中P1和P2上任意两点的关联。van Cittert-Zernike定理定义了部分同调的复合度即：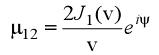
，其中 `H:5D5] 
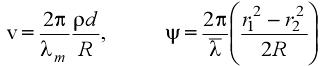，ρ为小孔σ1的半径，d为P1和P2的中心距，R是L1的透镜焦距，r1和r2分别为从光轴到P1，P2的距离，λm是平均波长。为了测试FRED的性能，我们计算了平面F上的辐照图的缺口长d与P1，P2之间长度距离的变化，得到了与after B.J. Thompson and E Wolf绕射仪相吻合的结果。测试时的参数模型是f1=f2=R=1520mm；L1，L2之间的距离为14mm；小孔面积的直径为90um；光阑P1，P2的直径为1.4mm；平均波长λm为0.579um。 7 fE
QD?C SP,#KyWP0)
[M7& QQ：2987619807 ]
X9e|
