-
UID：317649
-
- 注册时间2020-06-19
- 最后登录2024-11-22
- 在线时间1530小时
-
-
访问TA的空间加好友用道具
|
运用智能光线进行物理光学建模 @y5= J`@=
`w+1C&>^[ Frank Wyrowski and Christian Hellmann 2QL?]Vo
+j.qZ8 光线光学早在2000年以前就已经建立了光学建模和设计的基础。而在最近的数十年中，光线追迹软件的出现为我们带来了解决光学和光子学问题的强大的光学设计技术。然而，随着高级光源的开发和应用，微纳结构加工工艺的成熟以及各种应用和光学相关功能的增强，光线光学的限制变得越来越明显。因此，基于物理光学的光学建模技术变得必不可少，其也是未来光学设计软件开发中顺理成章的一步。这就要求我们将光线追迹推广并将其与衍射建模技术联合起来。 F\-Si!~oOz b)`pZiQP 在光线光学中，我们使用源于光源的光线来描述光。数学上，光线由位置和方向矢量来表示。光线传播通过介质，其光学“阻抗”通过折射率来描述。应用此概念，通过改变光线在空间的方向和位置矢量以此来表述光的传播。光在均匀介质中沿直线传播，不同介质间界面的折反定律和渐变折射率介质中的光线方程，所有这些光线光学的基本定律都可以从费马定律中得出。简而言之，即光线沿所需最少时间的路径传播。基于费马原理的光学建模构建了光线光学，从数学的观点出发，由于光线模型是一个几何概念，因此费马原理同样适用于几何光学。 *7Xzht&f xG1?F_] 光线追迹软件为我们提供了用以光线光学建模的数值工具。通过光学系统的3D光路是一个典型的通过光线光学研究方法获得的物理量。通过它，我们可以进一步得出任意平面和表面处的点列图，方向图以及光程（Fig.1）。这为我们提供了特别是进行透镜系统分析和优化所需的所有基本信息，其在光线追迹中大受欢迎。 o0l7 4 光线追迹法同样可应用于非成像光学。从而，我们需要考虑“能量相关的”物理量。如，辐照度。从光线光学来讲，这种局部的能量物理量是与光线的密度和方向相关的。 o<rsAe
n[P\*S Fig.1通过一个透镜系统的光路。在同样的系统中[4]可以看到电场分量。 Im+ 7<3Z
从光线到物理光学 Zw#<E
=\
m8+:=0|$ 直到现在，所有的效应和量都能够在几何光学的框架中进行表示。下一步中，我们探索在两种介质间界面的能量效应，例如，一个透镜的表面。众所周知，在界面处，一部分光被反射回去因此会造成透射部分能量的损失。4%是空气和玻璃介质间透射能量损失的典型值。似乎我们可以直接将这个值对每条光线的作用考虑进去，进而减少在探测平面的探测能量。然而，在我们简单的将此损失包含在光线追迹中之前，我们应该考虑其在光线光学，即费马原理中的正确性。在介质间界面4%的能量损失符合费马原理吗？答案是否定的，由于此原理仅处理光程，因此我们无法在光线光学的框架中找到这种表面效应的合理解释。在各种光学教科书中，你可以找到菲涅尔方程的推导，其给出了能量透射率T（透射比）和能量反射率R（反射比）的数学表达式[1]。此推导考虑的是理想电磁场平面波穿过两种不同折射率介质间的理想平面界面。这个结论使用了在平面界面处电场和磁场分量是连续函数的事实。由此直接推导出菲涅尔方程。而理想平面波以及连续横向场分量则来自于麦克斯韦方程组[2]。与完全基于费马原理的几何光学相比，我们是基于麦克斯韦方程组来考虑物理光学的。因此，应该依据物理光学来解释在两种介质界面处光能量的损失，并将其附加到光线追迹路径，已经引出了一种联合了光线和物理光学的算法。然而，当将传统的光线追迹强行的与一种基于物理光学的效应，如表面处的菲涅尔效应或者光线透过光栅的传输，联合起来的时候，我们会面临一个典型且严重的问题。即，除了入射光角度很小的时候，菲涅尔效应都是与局部偏振相关的。因此，为了精确地包含菲涅尔效应，简单的光线不够，我们还需要其偏振信息。读者可能会问道，那么光线追迹软件是以什么标准来处理那些问题。事实上是其不可能精确地处理光滑的或者光栅类型的表面效应，并且也没有包含偏振效应的模型。 ceG&,a$\ 传统光线追迹有许多限制，上文提到的仅是我们想要去克服的其中一种。我们所需要的是使用物理光学来表征光线。接下来我们会讨论从以几何光学为基础的传统光线过渡到在物理光学框架中使用的智能光线。 Bzw19S6y KUFz:&wK 几何场追迹 ^Q\X Gl K"w%n[u) Fig.2光线与光滑表面（左）、散射表面（中）和局部周期表面（右）的相互作用。使用局部平面波来表征光线。 + {e`]t>_ Fig.2演示了一束光线与曲面的相互作用。如果我们以电磁场平面波来解释一束局部光线且将界面局部地作为平面，那么可以局部地应用从物理光学所获得的理想平面波与理想平面界面相互作用的结果[3]。因此，我们开发出了一种用于这种局部电磁场平面波概念的算法，即几何场追迹[4]。此理论来自于《光学原理》[5]第三章所提出的结论，并且我们已经探讨了在几何场近似条件下使用几何场追迹[4]来求解麦克斯韦方程组。对于局部平面波，使用这种近似的方法来求解麦克斯韦方程组，可以给出波前为主导的场的空间演化区域的精确解。相反，若一个场的尺寸没有远大于波长，则其开始受衍射主导且不能使用几何场追迹来传播该场，而需要使用一个衍射场追迹的方法来进行传播。换句话说，一个场的散度可以用其波前的曲率（几何场追迹）或者通过横向和k空间维度间的不确定性原理的扩展（衍射场追迹）来控制。空间中的任意场都有其衍射的和几何的主导区域，对于不同的区域需要使用合适的建模技术。如Fig.3，对于传播经过其焦点的球面波。我们想着重的强调的是，我们已经应用了能够自动测试几何场近似有效性的算法以确保选取最合适的建模技术以用于传播的各个区域。 QZ~0o7
x[x(y{&~ 7 >bMzdH Fig.3 透镜系统出瞳处一个截锥球面波通过其焦点传播的严格一维计算。下图是上图焦点区域的放大。球面波的f/#为20。尽管其是一个旁轴案例，但衍射主要在焦点区域。 5gshKmt_ 在实际中通过追迹智能光线来实现几何场追迹，当在VirtualLab Fusion软件中使用时，可以获得以下特性： PS}73Y # 智能光线知道其位置处的所有电磁场信息，三个电场分量和三个磁场分量的振幅，相位以及偏振信息。 1'fb
@vO 智能光线知道并记住光源平面中附近光线的波前。这通过一种合适的光线索引概念（波前索引）来实现。这个方法联合了不同的横向插值技术以用于所用的场量并将这些场量分配到一条光线上去。插值技术包含了样条曲线插值和质心坐标网格插值。 3+V#[JBJv 伴随智能光线的还有另外一个索引概念（空间相干索引），其能够给出智能光线间的相干模式和非相干模式以及其组合模式。这使得我们可以完成对部分相干光的建模。特殊的情况也被包含其中，如完全相干光和非相干光。 N O4Z"3Pd_ 为了包含颜色，时间相干和超短脉冲，我们将频率分配给智能光线，使用一个索引概念来分辨稳态光和脉冲光的频率分布（频率索引）。 b
i~=x 通过追迹智能光线我们获得麦克斯韦方程组几何场近似的解[4]。因此，智能光线将传统光线追迹推广，并用一种科学地可靠的方式将其结合到物理光学建模中。实际上，至关重要的是几何场追迹获得电磁场结果和传统光线追迹获得的结果，如点列图的速度是一样快的。 F&az": 高精度的模拟透镜系统可以主要依据几何场追迹，由于透镜系统旨在传输球面波，因此几何场追迹近似是有效的。如Fig.4所示。智能光线追迹提供了位于最后一个透镜后的所有电磁场信息。然而，如前面所讨论的（见Fig.3），位于焦面区域的场不满足几何场近似。因此，使用智能光线在最后一个透镜后获得的场必须使用衍射技术传播到焦点。在标准的光线追迹软件中，这样的一个过程或多或少的依赖于软件包中的点扩散函数（PSF）和调制传递函数（MTF）计算工具来精确地完成。场追迹为此以及其他类似的建模任务提供了一种快速和可靠的物理光学建模策略。 RX>2 ~^ \0&SI1Yp Fig.4 上面一行显示的是x方向偏振光经过Fig.1中透镜系统的最后一个透镜后的电场分量E = (Ex,Ey,Ez)。结果包含了一个从x到y方向较弱的串扰和一个中等的z分量。此结果是通过几何场追迹法在近1秒内获得的。下面一行是将上面所获得的几何场追迹结果衍射传播到焦点所得到的结果。 9go))&`PJL
模拟散射，光栅以及衍射透镜 X!c?CL
fEwifSp. 追迹通过两种介质间的界面的智能光线为几何近似的有效性提供了一个简单的标准。由于智能光线知道其临近光线的波前，界面后光线的相交很容易地就被自动探测到。相交光线表明波前被破坏了，因此几何场近似不在有效（Fig.2，中图）。很明显地，当光学表面不是光滑且仅小范围的进行调制则光线会相交，例如，带划痕的透镜或者一个散射粗糙表面。此种情况下，光学界面后的光场需要一种衍射方法以用于继续传播。此时，我们完全得益于统一场追迹概念，其能够让我们结合不同的电磁场建模技术以用于系统不同的区域[6]。 ;7j,MbU 让我们仔细的看一下一个散射表面后的衍射传播技术。一般情况下我们可以使用傅里叶分析来将理想平面波分解以生成不同的传播积分来探讨这种情况。当然，每个平面波可以通过几何场追迹进行进一步传播，通过一个物理光学理由和策略将一条输入光线转换成大量的输出光线。如果我们假设光学界面至少是局部周期性的（Fig.2，右图），例如，一个光栅或者衍射透镜，依据光栅方程，那么仅在离散方向上才有平面波的傅里叶分析结果，如光栅级次。这就允许我们选择那些感兴趣的级次进行使用，如一个衍射透镜的第一级次。通过几何场追迹，就构建了一个光栅和衍射透镜的物理光学建模的简单说明：通过智能光线传播场到光栅或者衍射透镜，局部光栅效应使用电磁场分析，例如通过傅里叶模态法（FMM）[7]，然后由此产生的偏转的局部电磁场平面波通过智能光线追迹进一步传播。需要强调的是在模拟光栅和衍射透镜时，与传统光线光学的准确结合是无法实现的，而是要求智能光线提供必要的场信息以处理局部光栅效应。在VirtualLab Fusion中这项技术已经得到了应用，因此能够使用它来设计衍射透镜。然后，衍射透镜的结构可以以各种格式导出，如用于光刻的GDSII文件。Fig.5演示了一个用光栅将光耦合进和耦合出一个波板以用于色彩混合。 p9iu:MucD< )4m_A p\ Fig.5 通过一个光栅将RGB光源的光耦合进入一个波板，通过波板的全内反射进行传播，并使用三个光栅将光耦合出波板以获得一个部分重叠的混合色彩。本次模拟是通过FMM模拟光栅并使用几何场追迹的方法来完成的。上图显示了光线传播和几何场追迹结果。 ;_N5>3 C:
干涉和相干建模 Z0\Iyc G
<u0,Fp
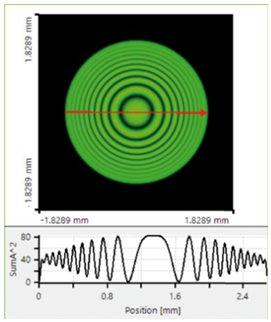J>h;_jA  QC7k~I8 Fig.6 Mach-Zehnder干涉仪对于一个时间部分相干光源的干涉图案。此建模是使用几何场追迹完成的，在PC上对超过100个波长进行计算，用时在1min以内。 FM\[]. F0.z i>5  Mk5RHDh Fig.7 对于一个不同厚度的薄膜，通过多重干涉所获得的反射光的强度结果。使用光源为RGB白光。建模使用的是几何场追迹，用时少于1min。 hKN6 y%
.iT4- 作者 'RLOV ti2
vD26;S.y[a
 ?cK]C2Ak
N RSU+D-z Frank Wyrowski是Jena的Friedrich Schiller大学的技术物理教授以及应用计量物理组的负责人。在1999年他合作创办了LightTrans公司，并于2014年联合创办了Wyrowski Photonics公司。他喜欢并致力于各种光学建模和设计任务，特别是物理光学领域。其研究成果源源不断地为光学设计软件VirtualLab Fusion的进一步开发做出贡献。 bV6V02RF
bVK$.*,
R=$Ls6z
"+h/-2rA
%l|\of7P2}
xS+rHC
D^?_"wjW
-oh7d $~
UA(;fZ @
lT ,+bU
[W;[v<E;
jQ$BPEG&X Oy$<QXj/  |Gu EGmR
$ $4W}Ug3U Christian Hellmann是Wyrowski Photonics UG的CEO并且负责VirtualLab Fusion的开发工作。他代表Bosch股份有限公司在Horb的联合教育大学完成他的计算机科学学习后加入到了LightTrans股份有限公司。在LightTrans公司其负责光学建模的编程和算法开发。从2013至2014年，其是LightTrans首席产品官。 9XO yj5
Dbz]{_Y;
7' eh)[T
hW'
HT
'9q6 aM/&
m UgRm]
z_l. V /G)
k
,fTW^ ?
HJ@ 5 B" l RND 参考文献 (oYW]c}G,
0p3vE,pF [1] E. Hecht and A. Zajac. Optics. AddisonWesley, 1974 /80YZ [2] J. D. Jackson. Classical electrodynamics. John Wiley & Sons, New York, 1975 D^$OCj\ [3] A.v. Pfeil, F. Wyrowski, A. Drauschke, and H. Aagedal. Analysis of optical elements with the local plane-interface approximation. Appl. Opt., 39(19):3304{3313, 2000.article KY+]RxX [4] F. Wyrowski, H. Zhong, S. Zhang, and C. Hellmann. Approximate solution of maxwells equations by geometrical optics. In D.G. Smith, F. Wyrowski, and A. Erdmann, editors, Optical Systems Design 2015:Computational Optics, volume 9360 of Proceedings of SPIE, page 963009, SPIE, Bellingham, WA, 2015, 2015 [h HG . [5] M. Born and E. Wolf. Principles of optics .Cambridge University Press, 1999 &yLc1#H [6] F. Wyrowski and M. Kuhn. Introduction to eld tracing. J. Mod. Optics, 58(5-6):449{466, March 2011 LdEE+"J w [7] J. Turunen. Diraction theory of microreliefgratings. In H. P. Herzig, editor, Microoptics elements, systems and applications, chapter 2, pages 31{52. Taylor & Francis, London, 1997 6mHhC? [8] Unied optical design software “Wyrowski VirtualLab Fusion”, developed by Wyrowski Photonics UG, distributed and supported by LightTrans GmbH, Jena, Germany r0btC@Hxy
qd(hQsfqYU
ikHOqJ-,m QQ：2987619807 D]u=PqHk2
|
