-
UID:317649
-
- 注册时间2020-06-19
- 最后登录2025-04-08
- 在线时间1761小时
-
-
访问TA的空间加好友用道具

|
用于模拟相干性的FRED工具 0Qeda��@J� ■ 相干光源 �Wwn�Be"7M FRED包括许多默认相干光源,包括:平面波、点光源和激光光束。一种详细的光源菜单可以轻松、方便的自定义光源。 �c��f>�l�Y ■ 高斯光线尺寸点列图 S����=V�� 高斯光束可以在任何平面上显示,显示每个基准光线和它的1/e2椭圆,便于光束发散度和采样的分析和故障排除。 "�8z�Me L ■ 光线状态概要 k�z��U�j�) 显示每一光线的状态,使其易于进行故障排除和诊断光线的错误。 *w�mkcifF; ■ 相干场重新采样 rm�vrv�.$3 对标量场在空间上重新采样可以避免相干光的错误和表面的采样不足。 yr>J^Et%_� ■ 相干场分析
E>*b,^J7g 显示标量或极化矢量场的幅度、能量、相位和波前图。 `��g(�#~0R ■ 波前计算 <bCB-lG*Kb 具有Zernike分解能力的波前分析和绘图。 CiH�x.5TiC ■ 部分相干性 avG#�0A�Y� 对于特定的应用,可以执行部分相干光源和分析。 @�|ZU�ya�t
!E00I0W-h
,*l��ns.|n
目录 $X.F�=Kv��
b9i��_���\
简介 �$$4f�l�fx
FRED基础:相干性建模 �!U(S?:hvW
锁定FRED特点:相干场重采样 Z \ ��@�9*
相干光源定义 �����W"#<r
高斯光线尺寸点列图工具 �O3sl�Yd&V
光线状态 zn�= p�m#L
相干场重新采样 ��FO!0TyQ�
相干标量场分析 �75R4[C6T
FRED中部分相干性示例:衍射仪 JF}i�=}���
�Dv�z 6 E� 简介 oui0:�V�y<
(?XI�hp��d 模拟光线的相干特性非常意义的。当用FRED模拟相干系统时,用户应该对FRED进行相干计算的方法有一个大致的了解,它是利用高斯光束分解(GBD)的一种一般形式。本应用描述了一些在使用FRED时基本的相干建模方法和注意事项,以及一个应用于ThorLabs扩束器的相干场重新采样特性的一个示例,最后,衍射仪用于演示一个部分相干性模型。 \�?e2qu/ C
;{iT�S�sb
M�x93�D
�
FRED基础:相干性建模 �oli�Vaavj
k��"�BM1-f
FRED关于激光光束的追迹采用高斯光束分解技术(Gaussian beam decomposition,GBD)来传输相干场,最早由Arnaud 在1969年提出,是一组高斯光束子波(beamlet)可以合成任意的复数场。传统的GBD方法局限在两种极端情况下,一种是空间分解法,子波均匀分布在格子点上,另一种是傅里叶分解,根据空间频率谱分解为在一个空间位置具有不同相位和方向的子光束。对此,Gabor对Arnaud的方法进行了扩展,并用在FRED中,允许这两种方法结合起来以一种更加灵活的方式来拓宽使用条件。 lei�z�jL\P
d9e~>�<bPJ
在FRED中,由高斯子光束的叠加来描述光的的传播。中心的“Base”光线代表着子光束的传输轨迹,额外的二级“束腰”和“发散”光线记录子光束参数的变化。子光束和它对应的光线的关系如下图所示。当子光束经过折射、反射和衍射,这些光线完全描述了该子光束特性,因此这个过程被称为“complex raytracing.”。在系统中的任何平面,通过确定在分析面上的每个位置处每个子光束的贡献和对相位的比例来计算相干场。 �{#z47Rz�
t�*BCpC��}
因为它们是高斯型的,子光束服从与远场发散半角θ和最小束腰半径ω0有关的方程(其中λ是波长,n是介质的折射率): 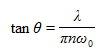 (1) fIx|0,D&7L
子光束的半径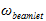 在传播过程中变化,与束腰光线高度hw和发散光高度hd有关: 在传播过程中变化,与束腰光线高度hw和发散光高度hd有关: 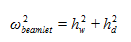 (2) O7��Jp��;�
K|�~�!o�Q�
其中光线高度相对于Base ray。 ���O@H�D�'
"AMw��o(Yi
为使模型变得精确,它们必须要保持高斯型并遵循近轴近似,这是相干光线追迹中最重要的考虑因素。尝试在近轴限制之外操作高斯子光束传播会使准确性大打折扣。二级光线未能保持与它们的Base Rays好的相关性可能会导致相干光误差和错误的辐照度计算。 ~^Ga?Q�_�
Z
*l&<�q>#
虽然没有精确的定义,近轴近似可以使用至少两种形式描述: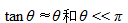 。在这两种情况中,对于 一个合适的选择是0.1弧度,大约为6度。根据公式1,近轴近似最明显的隐意是子光束的束腰半径ω0必须大于等于3 。在实际使用中,用户应该考虑具有一定余量的操作,可能是5-10 。通过追迹二级光线并计算光学不变量H’nU - HnU’(其中H是光线高度,n是材料折射率,U是 。在这两种情况中,对于 一个合适的选择是0.1弧度,大约为6度。根据公式1,近轴近似最明显的隐意是子光束的束腰半径ω0必须大于等于3 。在实际使用中,用户应该考虑具有一定余量的操作,可能是5-10 。通过追迹二级光线并计算光学不变量H’nU - HnU’(其中H是光线高度,n是材料折射率,U是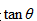 ),FRED记录了子光束的相位。如果对于一个给定的相干光线不变量超出了 ,则用于计算的光线会被告知无效。不变量作为一个内部尺度,告诉了子光束的好坏程度。 *}(�B"FSO� ),FRED记录了子光束的相位。如果对于一个给定的相干光线不变量超出了 ,则用于计算的光线会被告知无效。不变量作为一个内部尺度,告诉了子光束的好坏程度。 *}(�B"FSO�
pG�*���W>F
当定义好一个相干光源,FRED设置了一个光线网格,并使用网格间距 (这是网格的宽度 被穿过网格的光线数 划分所得),和一个光束重叠因子(OF)来设置子光束的束腰半径 ,如方程3和4所示。随机光线网格不应该被用于相干源,因为网格间距不均衡,将会产生不同的束腰半径。对于网格宽度和光线数中的x和y值可单独控制。在FRED追迹光线的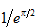 点处,子光束的束腰半径是: 点处,子光束的束腰半径是: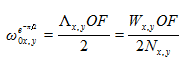 (3)
使用更常见的 束腰半径惯例增加了一个额外的因素, 束腰半径惯例增加了一个额外的因素, 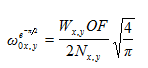 (4) ��Td^62D�;
重叠因子是在网格上相邻子束之间的部分重叠,并具有1.5的默认值(很少改变)。因此,要保持 的近轴限制内,对于可见光(λ=0.5 μm),网格间距应该是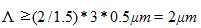 ,一个更加合理的范围为5-10μm。 =.m�/�X��> ,一个更加合理的范围为5-10μm。 =.m�/�X��>
8BS� �N�m�
锁定FRED特点:相干场重采样 :N<o�<�qn
:u@ �w���;
有某些情况下,当使用正确定义的相干光源仍然会导致相干光线的错误。在这个例子中,一个Thorlabs 5倍扩束器(BE05M)用来演示FRED的相干光场重采样特征,以及其他一些有用的工具。 n^G[N-�\�3
�(�]fbCH�:
通过导入由Thorlabs提供的CAD文件,并且用FRED自带的透镜元件及光学特性来代替光学CAD部分,我们可以在FRED中模拟扩束器。图2显示了使用3D剖面图显示系统布局。 5��|�bf�rc
图2 一个Thorlabs 5倍扩束器的FRED模型。FRED的3D剖面图用于显示外壳的内部构造。 NgxJz
��]b
��?5�pZp~
相干光源定义 P�a|*�Jcr�
���0!:%Ge_
在FRED中有一些默认的光源,包括平行光源,点光源,高斯TEM00模激光束和激光二极管光束。相干的高斯He-Ne激光束用于这个例子。一个高斯光束的输入参数有光束大小(束腰半孔径)、网格大小(在采样平面处的腰部半孔径)和整个平面上点的数目。一个好的经验法则是设定光束大小(束腰半径)为网格尺寸的一半。在这个例子中,光束被定义为圆形,在2mm*2mm的每个方向有41条光线穿过的网格上(W),束腰半径是0.5mm(直径1mm)。这是一个完全有效的相干光源定义。它的子光束有大约41.7μm的束腰半径,远大于6.328μm的10 边界;同时有0.28°的发散角( ),远小于6°的近轴限制。 rO1N@�kd�/
Iz#jR2:yn�
在 点(方程4)处的束腰半径是: @WKJ7pt`'N
�9Z�� ��6�
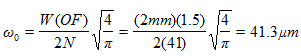 l0',�B*�og l0',�B*�og
)�T(1oK(g�
子光束发散角为: ?LvxEQ�-�g
fE>Jo�Qs38
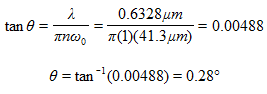 h2+"�e#� _ h2+"�e#� _
e<u~v0r�Dl
高斯光线尺寸点列图工具
a(`"q�S��
g�d]k3XN$f
FRED的高斯光线尺寸点列图工具对于检验高斯子光束特性、可视化二级光线位置和诊断相干光线的错误非常有用。该工具利用对应的1/e2椭圆来绘制基准光线。尽管没有明确绘制,二级束腰光线沿着该椭圆一般有4个,在 和 方向。FRED在高斯光线尺寸点图中绘制了一个1/e2束腰光线椭圆,但是在光线追迹中使用了沿着稍小的1/eπ/2椭圆的二级光线。图3显示了在两个位置处激光光源的高斯点图:(a)在光源处,(b)在下游的650mm处。基准光线是完全准直的,但激光光束本身是发散的,这可以通过注意1/e2椭圆(在这种情况下圆形)已传播650毫米后尺寸的增加来观察。 C6tfFS3b�q
图3 高斯光线尺寸点列图,放大的中心用以显示细节。(a)在光源位置。(b)当光束传播了650mm后,轮廓如最右边的子光束。基准光线准直,二次光线发散。 A4�L�.bB�l
\/�Z��o�*/
假设扩束器是光学系统的一部分,它需要第一表面距离激光源650毫米。一个例子是马赫泽德干涉仪,在其臂处有不同的光束尺寸,如图4所示。 #K>�Ue>h�x
图4 马赫泽德干涉仪的FRED模型,在一个臂处有扩束器。 shY8h
����
mI�;\ UOh'
仔细观察图3b,发现子光束轮廓直径大约是6mm。扩束器的发散透镜只有5mm的直径。因此推断二级光线被略去的似乎是合理的,但情况并不是这样的。复合光线追迹的基本准则之一是:如果基准光线与一个表面相交,然后所有它的二级光线一定与同样的表面相交。通过在数学上延展表面与每个二级光线相交,如图5所示,FRED强制执行该准则。当执行光线追迹时,所有的光线通过该表面。 �Ci3
b(KR�
图5 光学表面的数学延伸算法,用于与不和实际表面相交的二级光线相交。 u�b4(�g�~E
K1-��3!G��
有三种类型的相干光线的错误(在下面的部分中讨论),如果它是不能正确地传播的光线,在光线追迹后,FRED只显示了一个警告。就好像如果它无法在数学上延伸必要的表面,它就会发生。在执行分析时,另外两个相干光线错误只会产生一次警告。在扩束器的情况下,该追迹的光线没有错误或警告,这是由于透镜的球面很容易扩展。但是当执行分析时,问题升级了,因为二级光线不再与基准光线良好相关,子光束从完美的高斯型变成了过于发散。 V��-du�b{K
ZtI@��$ An
光线状态 $D*�Yhv�!/
Ivq|-�LDNc
FRED的光线状态工具处理问题非常方便,如该扩束器模型,其中有一个问题,但细节和原因还不清楚。光线状态会输出目前系统中所有光线的状态,如图6所示。有三种类型的相干光线错误: �CSFE�[F63
1.相干二级光线追迹错误(Coherent secondary ray raytrace errors:):这表明,在光线追迹的过程中,发生了一些事件阻止了所有光线被正确追迹。在光线追迹完成后,描述了特定问题的一个警告呈现在输出窗口的光线追迹摘要中。举个例子,如果一个基准光线穿过了一个球透镜,但是二级光线与该透镜没有相交,延伸光学表面使得二级光线产生相交是不可能的,然后FRED会输出如下的消息:“Rays halted because unable to complete coherent secondary ray intersection(warn: 18)”。 \���tU[,3
2. 相干二级光线不变量违规(Coherent secondary ray invariant violations):当子光束偏离高斯光束太远,这个错误就会产生。当光线追迹完成时,没有错误或警告,尝试分析时会产生一次。 �"�@xL9�[d
3. 相干光线高斯指数衰减违规(Coherent ray Gaussian exponential decay violations):此错误非常类似于前一个,但表示该子光束已经变得太发散。直到尝试分析时,才会报告一些错误或警告。 9.Sv"=5gz�
��y�W}x���
在扩束器的例子中,所有1313条光线违反二级光线不变量和高斯指数衰减,因此是无效的。如图6所示,概要显示了在光线追迹过程中可能产生的错误,这在对系统进行故障排除时作为切入点是很有用的。 �~^g*cA
t}
图6 输出窗口显示了光线状态概中相干光线错误要结果 Q�A~L��m�
z Hl+�P*)�
相干场重新采样 P��[����,�
c#�fSt}J>C
相干光场重采样特征可以用来解决相干光线的错误,通过计算和产生一组新的在扩展空间区域重现当前标量场相干光线。新光线归纳起来产生相同的场,但新合成的子光束重新定义了束腰和发散角。这类似于产生具有性能良好的子光束的一个全新的光源。面积、像素大小和重新采样网格的位置由一个分析表面实体指定。这些参数,就像是光源创建网格,决定了子光束的属性。因此,在定义一个光源时,关于像素尺寸和间距应该有相同的考虑。相干光场重采样执行以下操作:波前计算,任何球形和倾斜项的去除,光场的重新采样,球面和倾斜项的合并,在分析表面上每个像素的中心创建一个新的子束来再现原始光场。相干光场重新采样对话窗口如图7所示。 Ht~YS�Q~:y
�E�u�D$^#�
在此扩束器的例子中,光场的重新采样就在与原始光源具有相同的光束参数的第一个(发散)透镜的前面,因为它已经确定该束腰和发散是合理的。我们创建了比发散透镜(半孔径2mm)的尺寸略小的分析面,调整分割数来产生于初始光源(73)相同的束腰。这种调整是有必要的,因为初始光源是定义在圆形网格上,而新的光场是定义在方形分析表面上。 I�g�e*tOv2
Oh7w�yQiV�
使用高级光线追迹功能,追迹从光源到第一个透镜的光线,该功能可以在光线追迹的过程中实现精确的控制,包括在特定的平面上停止光线追迹。然后光场可以被重新采样(Raytrace > Spatially Resample Scalar Field…),删除现存的光线,并用新定义的光线替换它们。重新采样场应该与初始场相同,唯一的不同是用于定义它的光线。然后使用Trace Existing Rays或Trace and Render Existing命令,追迹系统剩余部分的光线。 J>0�RN/38o
图7 光场重新采样功能对话框 T'14OU2N{Y
X'7MW?
�q@
除了解决相干光线错误,相干光场重采样也可以在一个表面欠采样是的情况下使用。例如,如果扩束轨迹长度很大,第二透镜将满溢和欠采样,如图8所示。因为前面所描述的最小网格尺寸的限制,从而增加源光线的数量不是一个合适的解决方案。相干光场重采样特性可用于在第二透镜处重现光场,并合成具有透镜的足够空间采样的新光线网格。 VQ2�B��|�v
图8 大倍率远焦望远镜致使第二透镜的欠采样。 Y^5)u/Y�=U
M�nW"k�sH�
相干标量场分析 +L=a�\8�Ep
n1y*`5��!
新光线合成之后,它们可以通过系统被追迹,而没有相干光线错误,所得到的场可以分析。相干光场的能量、相位和波前可以用相干标量场分析工具进行研究。图9显示了具有用红色框出的可用绘图选项的标量场菜单。它也给出了用于显示和输出图像、缩放数据、平滑和修改图像数据、显示图像统计和执行一个傅立叶变换的选项。图10显示了在扩束器输出处的场能量、相位和波前。 �AT"�!�Ys|
图9 当右键点击图像时显示的标量场分析菜单,红框显示为可用绘图。 uX&Tn�1Kg�
图10 FRED输出图像,显示a)场能量、b)场相位、c)波前 ��pm*i!3g'
:rN5H�Og^9
FRED中部分相干性示例:衍射仪 M�9(Kx�ux#
��Rd��y-6�
用FRED可以模拟部分相干光源,通过集相干的点源为一体,每一个都具有不同的空间位置和波长。在FRED部分相干的建模被限制在特殊情况下,这样的定义才是有效的。 [ldx_+xa:E
^F�+7@*��u
类似上述的一个例子是衍射仪,可用于测量光源的空间相干性的干涉仪。本例是基于由Thompson和Wolf[1]描述的设置,如图11所示。一个扩展的非相干的光源 ,通过一个透镜 成像,聚焦到一个小孔 上。由 产生的光经过 准直和 聚焦到平面F上。含有两个小孔 和 的不透明的屏A位于 和 之间。孔径可以是任意的尺寸和形状,可以放置在平面A上的任何位置。 4���m_CPe�
图11 衍射仪 �8H{�����9
04�!ak�PP<
图11的轮廓断面可以在FRED中通过在小孔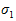 上不同波长、随机位置的点光源的聚集来建模。如果波长在一个小的带宽内,这一光源的聚集满足一个由Born & Wolfe [2]给出的准单色光的定义。对于这个例子,使用了在0.579±0.002μm内的波长。光源的每个波长分量在平面F上独立生成一个干涉图样。FRED归纳了相同波长的相干性和不同波长非相干性。因此,在平面F上总辐照图案是每个波长独立相干成分的非相干总和。 o5��w�� =� 上不同波长、随机位置的点光源的聚集来建模。如果波长在一个小的带宽内,这一光源的聚集满足一个由Born & Wolfe [2]给出的准单色光的定义。对于这个例子,使用了在0.579±0.002μm内的波长。光源的每个波长分量在平面F上独立生成一个干涉图样。FRED归纳了相同波长的相干性和不同波长非相干性。因此,在平面F上总辐照图案是每个波长独立相干成分的非相干总和。 o5��w�� =�
h]�^=
y.�Q
因为只有小部分光线通过了小孔p1和 p2,所以上面描述的光线追迹是非常低效的。一个可以获得相同结果的更加高效的方法是在透镜 前面定义两个光线的圆形网格。光线网格应类似于两个小孔(在x-y平面上有相同的间隔和位置),但尺寸稍大,以确保光线溢出小孔。两个圆形光源的光线方向被指定为从孔径 内的随机位置始发。FRED有一个选项用于指定光线的方向,称为Focus to/from a point,这会产生由用户定义的聚焦到一个点或从一个点出发的光线。这两个光源都在以稍有不同的波长处创建了许多次,每一组网格定义成在 孔径的随机位置出发。图12显示了两组光源,有延伸回到所述孔径的光线和一个有限数量的光线,以帮助展示光源的创建。总结这一过程,孔径 中的一个随机位置被选择。两个光源分别对应于小孔 和 (组成光源集),就定义在第一个透镜前面。对于两个光源的光线方向,指定为起源于所选择的随机位置。然后选择另一个位置,创建两个或更多的对应光源。对于许多光源,重复这一过程。在本例中,使用一个内置脚本创建了75组这样的光源。目标是在小带宽内的任意位置和波长处,仿真许多点光源,它们已经传播到刚好在 前面的两个区域,这样它们就覆盖了小孔 和 。图13显示了衍射仪的FRED模型。在第一个透镜前面创建了光线,但是它们已经扩展到 便于视觉表现。这一选项叫做Post-Creation Ray Propagation,在像这样的情况下是有用的,它有助于可视化实际上不存在的光线。 |�+aD%'��|
图12 创建的两组光源类似于两个小孔,光线方向从左侧的孔径的随机位置过来。不显示透镜是因为便于小孔的显示。 n_t.l<���V
图13 衍射仪FRED模型。通过变形三维视图(Anamorphic 3D View. Anamorphic 3D View.),系统已缩小Z方向以提供整个系统的视图。 -��lI6!a^�
��=K6{AmG$
根据van Cittert-Zernike理论,1934年经P.H. van Cittert独立发展,后来到1938年又由F. Zernike发展,在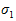 处的光源聚集提高了屏A上任意两点p1和p2处场的相关性。van Cittert-Zernike理论建立了部分相干的复杂度如: 处的光源聚集提高了屏A上任意两点p1和p2处场的相关性。van Cittert-Zernike理论建立了部分相干的复杂度如: 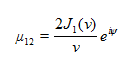 (4) ']�>/�$[�!
其中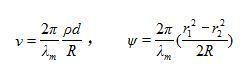 (5,6)
J1是一阶第一类贝塞尔函数, p是小孔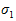 的半径,d是p1和p2之间中心-中心距离,R是 的焦距长度,r1和r2是p1和p2偏离光轴的距离, 的半径,d是p1和p2之间中心-中心距离,R是 的焦距长度,r1和r2是p1和p2偏离光轴的距离, 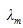 是平均波长。 是平均波长。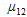 的振幅被称为空间相干度 的振幅被称为空间相干度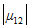 。 �f_r4�*#&v 。 �f_r4�*#&v
X�}]g;|~SN
我们调查了小孔间距d对空间相干度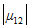 的影响。在仿真中使用了以下的值: p=0.045mm,R=1505.6 mm, r1=r2=0(在轴上), 的影响。在仿真中使用了以下的值: p=0.045mm,R=1505.6 mm, r1=r2=0(在轴上), 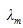 =0.579μm。 =0.579μm。 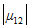 对d的依赖性是振荡的,这是由于如图14所示的贝塞尔函数。对于四个小孔间距(在图14中通过点标记),通过FRED建模,它们在平面F上的干涉图样显示在图15中。FRED的仿真结果与Thompson and Wolf的结果吻合良好。 ��.$r7�q�[ 对d的依赖性是振荡的,这是由于如图14所示的贝塞尔函数。对于四个小孔间距(在图14中通过点标记),通过FRED建模,它们在平面F上的干涉图样显示在图15中。FRED的仿真结果与Thompson and Wolf的结果吻合良好。 ��.$r7�q�[
{9h`h08?z�
当两个小孔处的强度相等并且时间相干性可以忽略时,这里就是这种情况,条纹可见度等于部分相干度。条纹可见度定义为: 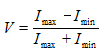 (7) wB%;O�`�Oh
其中Imax和Imin是条纹辐照度的最大和最小值。将FRED模型与部分相干度的理论值比较,使用中心条纹的最大和最小辐照度值,估计四个小孔间距每一个的条纹可见度。在图14中红色的X对应于估计的条纹可见度,这是基于图15所示的干涉图样。正如图14和15所示,基于FRED模型的近似值合理的靠近理论值。 �q>�d�ERN&
}�H9V$~}@-
图14 衍射仪的部分相干度vs小孔间距。点代表在FRED模型使用的设置处的理论 值。红色X对应于条纹可见度(等于 ),这是基于FRED图(如图15)计算得出。 HVM(L�Hm=:
A!_yZ|)$�T
图15 四个不同小孔间距d在平面F上的条纹可见度,以及对应的部分相干度 和估计的条纹可见度V。 f�:/"O�Cig
ID$�%4j�l
参考文献 �C,dRd�EB>
Wg=4��`&F^
1. B.J. Thompson & E. Wolf, J. Opt. Soc. Amer., 47 (1957), p.895. �}Ld�eU:E4
2. Born & Wolfe. Principle of Optics (6th Ed), Pergamon Press, Ch. 10, Sec. 4.3, p. 513 Q�r*�7bE(a
3. Hecht, Eugene. Optics (4th Ed), Addison Wesley, Ch 12.3, p. 571 K�]Z];C�#)
�|��F?�/L>
QQ:2987619807 d�/`�d�:g�
|