-
UID:317649
-
- 注册时间2020-06-19
- 最后登录2025-04-02
- 在线时间1761小时
-
-
访问TA的空间加好友用道具

|
POL RIBES-PLEGUEZUELO,1,2,*SITE ZHANG,2ERIK BECKERT,1 RAMONA EBERHARDT,1FRANK WYROWSKI,2AND ANDREAS TüNNERMANN1,2 fy�@�a�vo9 1 Fraunhofer Institute for Applied Optics and Precision Engineering IOF, Albert-Einstein-Str. 7, 07745 Jena, Germany 0�`.��^MC?
2 Institute of Applied Physics, Abbe Center of Photonics, Friedrich Schiller University Jena, Max-Wien-Platz 1, 07743 Jena, Germany *pol.ribes@iof.fraunhofer.de �]�$�afC!Z g���,`A[z2 摘要 I jr\5FA[p
.Xm(D>�>�k 提出了一种用来仿真激光晶体封装技术中的诱导应力的方法,并对激光腔内部的双折射效应进行研究。这种方法已经由软件ANSYS 17.0通过热机械仿真来实现。ANSYS的结果稍后被导入到VirtualLab Fusion软件中,这款软件按照波长及偏振性对输入输出光束进行分析。研究是建立在一种用于玻璃或晶体光学封装中低应力焊接技术,也被称作焊机泵浦技术的背景下。分析结果表明对于由钇铝石榴石活性激光晶体构建的激光腔,二次谐波发生器β-钡硼酸盐,以及由低应力焊机泵浦技术组装的熔融石英的输出激光镜来说,输入及输出激光光束几乎没有差异。 hc
��(e$## ○c2017 Optical Society of America OCIS codes: (140.0140) Lasers and laser optics; (220.0220) Optical design and fabrication; (260.1440) Birefringence. � $p!y�hn7 �gK#mPc�n^
参考及链接 ��U~{du�;\
^�Jb�
H? 1. S. Ferrando, M. Galan, E. Mendez, E. Romeu, D. Montes, A. Isern, M. Jardi, J. Juliachs, G. Viera. “Innovative optical techniques used in the Raman instrument for Exomars,” in ICSO International Conference on Space Optics,Greece 2010. (npj_s!.C) 2. P. Ribes-Pleguezuelo, C. Koechlin, M. Hornaff, A. Kamm, E. Beckert, G. Fiault, R. Eberhardt, A. Tünnermann,“High-precision optomechanical lens system for space applications assembled by a local soldering technique,” Opt.Eng. 55(6), 065101 (2016). T +5X0 �Nv 3. E. Beckert, T. Oppert, G. Azdasht, E. Zakel, T. Burkhardt, M. Hornaff, A. Kamm, I. Scheidig, R. Eberhardt, A.Tünnermann, F. Buchmann, “Solder jetting–a versatile packaging and assembly technology for hybrid photonics and optoelectronical systems,” in Proceedings of IMAPS 42nd Int. Symp. on Microelectronics, California, (2009) pp. 406. kK���8�itO 4. W. Koechner, Solid-State Laser Engineering (Springer, 1999). YD�C mI@� 5. C. Rothhardt, J. Rothhardt, A. Klenke, T. Peschel, R. Eberhardt, J. Limpert, A. Tünnermann “BBO-sapphire sandwich structure for frequency conversion of high power lasers,” Opt. Mater. Express 4, 1092 (2014). wIkN9
f��� 6. J. F. Nye, Physical properties of crystals (Oxford Universty, 2010). yJuQ8+vgR} 7. Q. Lü, U. Wittrock, S. Dong, “Photoelastic effects in Nd:YAG rod and slab lasers,” Opt. Laser Technol. 27(2), 95–101 (1995). _0+0#! J�! 8. G. Golub, and F. Charles, Matrix Computations (Johns Hopkins University, 1983). 7�\_o.(g#- 9. H. Bremmer, “The W.K.B approximation as the first term of a geometric-optical series,” Commun. Pure. Appl. Math. 4, 105–115 (1951). b[��z]C�P 10. F. Wyrowski and M. Kuhn, “Introduction to field tracing,” J. Mod. Opt. 58, 449–466 (2011). ��f)]%.�>� 11. D. W. Berreman, “Optics in stratified and anisotropic media: 4 × 4-matrix formulation,” J. Opt. Soc. Am. 62, 502–510 (1972). h%�WE=\,Qp 12. G. D. Landry and T. A. Maldonado, “Gaussian beam transmission and reflection from a general anisotropic multilayer structure,” Appl. Opt. 35, 5870–5879 (1996). ��5<�I� � 13. L. Li, “Reformulation of the Fourier modal method for surface-relief gratings made with anisotropic materials,” J. Mod. Opt. 45, 1313–1334 (1998). w�B'zuPAK6 14. L. Li, “Note on the S-matrix propagation algorithm,” J. Opt. Soc. Am. A 20, 655–660 (2003). y"�]�n:M:( 15. Physical optics design software “Wyrowski VirtualLab Fusion”, developed byWyrowski Photonics UG, distributed by LightTrans GmbH, Jena Germany. http://www.lighttrans.com. B1]�bRxwn? 16. S. Zhang, Applied Computational Optics Group, Institute of Applied Physics, Friedrich Schiller University Jena,Max-Wien-Platz 1, 07743 Jena, Germany, C. Hellmann and F. Wyrowski are preparing a manuscript to be called 8�0A.<=(=. “Algorithm for the propagation of electromagnetic fields through etalons and crystals.” Y|���8v�O 17. D. Eimerl, L. Davis, S. Velsko E. K. Graham A. Zalkin, “Optical, mechanical, and thermal properties of barium borate,” J. Appl. Phys. 62, 1968–1983 (1987). gTRF^knr�Y 18. W. Martienssen, H. Warlimont, Springer handbook of condensed matter and materials data (Springer, 2005). �aA�7�=q�= 19. I. H. Malitson, “Interspecimen comparison of the refractive index of fused silica,” J. Opt. Soc. Am. 55, 1205–1209 (1965). L
��lqM �c 20. W. L. Bond, “Measurement of the refractive index of several crystals,” J. Appl. Phys. 36, 1674–1677 (1965). ��6y�%0`!� 21. V. G. Dmitriev, G. G. Gurzadyan, D. N. Nikogosyan, Handbook of nonlinear optical crystals (Springer, 1999). \~P=U;l=pO 22. D. Asoubar, S. Zhang, F. Wyrowski, M. Kuhn, “Laser resonator modeling by field tracing: a flexible approach for fully vectorial transverse eigenmode calculation,” J. Opt. Soc. Am. B 31(11), 2565-573 (2014). y�H]�[(o=2 23. D. Asoubar, S. Zhang, F.Wyrowski, “Simulation of birefringence effects on the dominant transversal laser resonator mode caused by anisotropic crystals,” Opt. Express 23, 13848-3865 (2015). }@i�f�6(0� 24. D. Asoubar and F. Wyrowski, “Fully vectorial laser resonator modelling of continuous-wave solid-state lasers including rate equations, thermal lensing and stress-induced birefringence,” Opt. Express 23, 1880218822 (2015). A!1��;}�x� 25. P. Ribes-Pleguezuelo, A. Moral, M. Gilaberte, P. Rodríguez, G. Rodríguez, M. Laudisio, M. Galan, M. Hornaff.E. Beckert, R. Eberhardt, A. Tünnermann, “Assembly processes comparison for a miniaturized laser used for the Exomars European Space Agency mission,” Opt. Eng. 55, 116107 (2016). z��MIT}$L�
�+cb6??�H 1. 简介 jY�N�rD"�n
No2b��"�G@ 现今,激光设备广泛分布在不同的市场领域。现有的不同激光市场应用已经将对激光设备的要求推向了紧凑型、高效率和高可靠性的高度严格要求,以便能够在不同的设备条件下有效执行。此外,在汽车市场或太空应用领域中对激光设备的使用,一直在挑战激光制造商来获得在极端情况下也能够使用的更可靠紧凑的激光设备[1]。在获得具有高可靠性和高效率的微型化装置的情况下,最好的选择仍然是由胶粘剂组装成的二极管泵浦固体激光器(DPSSL)。然而,设备需要高的运行和存储温度范围,自由释气或真空兼容性,更高的热导率和电导率,甚至抗辐射组件,都导致需要寻找新的连接技术。目前有几种低压焊接技术可以用于此类设备[2]。然而,为了不损害器件的小型化,同时提供无应力的激光束谐振腔,我们必须研究封装诱导应力和随之而来的激光元件双折射现象。在本刊物中,我们研究了低应力封装激光焊接泵浦技术所产生的激光晶体的应力封装效应,此外,该方法也适用于其他激光设备的封装技术。 B^��).BQ��
rD>*j~_+�P 所谓焊机泵浦技术(图1)使用由各种软焊料合金(如锡基无铅焊料、低熔点合金或高熔点共熔合金金-锡,金-硅或金-锗焊料) 制成的直径范围为40至760μm的球形焊料预成型件。为了能够通过焊接技术将玻璃或晶体连接到金属或陶瓷基板上,这就要求将可附着的金属层涂覆到光学元件上,可通过物理汽相沉积(PVD)实现[3]。 @FdS��FQ/9
c��1X1+�b, 尽管这种技术保证了热能的局部化和最小化输入,使其适于连接玻璃或我们对激光晶体的研究案例,但仍必须分析诱导应力防止可能的激光谐振器运行不当,引起激光的光束质量或最终功率下降。 f�s/*V�~�@ �Q)�"A-�"y 图1.球形的软焊料合金从焊球存储槽转移到喷丝毛细孔,直到它们熔化并喷射到需要连接的部件为止。焊接装置安装在能够以6个自由度焊接部件的机械臂上[2]。 <d�yewy*.L
2. 仿真方法 Uye|9/w8 !
8Sz}�)U�Z 就我们的研究而言,我们选择了由DPSSL器件中最著名和最常用的激光材料代表的平面-平面激光腔(图2);钇铝石榴石或掺钕钇铝石榴石活跃晶体(Y3Al5O12),一个二次谐波发生器(SHG) β−钡硼酸盐(β−BaB2O4或偏硼酸钡),以及最后一个由熔融石英(二氧化硅)制成的输出二向色激光镜。所选用的软焊料合金是SnAgCu(SAC),用于将激光元件连接到氮化铝基板(AIN)上。 54zl�nM�$ [qsEUc+Z.' 图2所示,DPSSL腔的示意图。一个808nm的泵浦二极管,以及由三个组件表示的平面-平面激光腔;YAG晶体,SHG BBO和输出反射镜。 �5zON}"EC�
首先通过ANSYS 17.0软件用有限元法进行模拟,重复晶体的封装过程并计算出诱导应力。然后,通过每个组件的压电张量,计算应力引起的双折射被转换成电介质矩阵,最后被导入到VirtualLab Fusion软件来研究封装元件产生激光的能力。 Vh>Z,()>>@ b�Lt�.O(T}
2.1 通过ANSYS进行FEM仿真 %�`Z!��4L�
P�2�Vg�4 � 为了简单起见,光学组件被创建为由两个直径760μm 的SAC合金球体所焊接的独立的2 mm3立方体,并通过ANSYS设计模块融化到一个5×5×0.25mm的AIN基板(图3)。接下来,如表1和2中所示,对每个组件的材料属性进行定义。至于焊接合金,我们并没有做一个从液体到固体的完全的相变过程,因为这将增加模拟的复杂性,而是如表2和图4所示的在分析中包括了一些与温度有关的机械特性。 �fNGZ���o�
`y+�tf?�QN 图3所示,为每个激光元件设计几何形状的一个例子。比如SHG BBO晶体,它是由使用两个不同的坐标系统(晶体学和实验室坐标系统)来设计的。这两种不同的坐标系统能够定义材料正交的特征(见表1),而且也可定义SHG所需的晶相匹配角22.8° [4]。 �&�/,|+U�[
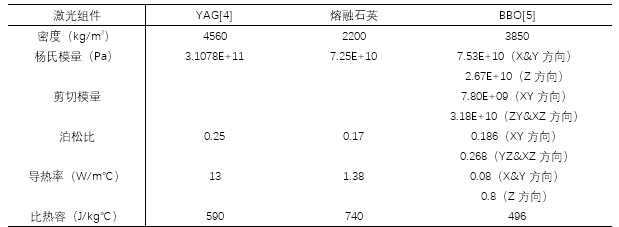
表1 使用激光材料的主要物理性质 r'gOVi4t1* �F;^F�+�H�
 C�]Q�8:6�b C�]Q�8:6�b
k�4 F"'N�� 稍后一个有限元瞬态热分析被耦合到一个ANSYS中的静态结构分析器,来研究SAC合金 (近似熔化温度217 ℃)从230℃ 到22℃的冷却过程,以及因此产生的组件装配中的诱导应力。利用后处理分析,从激光元件内部的光束路径中提取出矢量主应力,以研究器件的双折射和可能出现的激光偏置。 F�5S@I�; � DBP9{� x$� "Ks,�kSEzu 表2 焊接合金以及基板的主要物理性质 �Sna�4wkbS \�W��1/p`�  uslQ*�7S[^ ^pHq66�d%Z uslQ*�7S[^ ^pHq66�d%Z 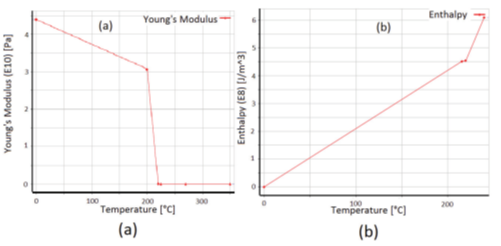 6;b�~�H�t� 6;b�~�H�t� 图4所示, 热依赖的机械材料性能。在图(a)中,各向同性弹性,杨氏模量。在图(b)中,合金相变焓。从塔拉姆仪器公司(法国)的实验数据中提取了合金热依赖特性。 ;;&}5jc�V� |JCU<_���< 2.2 应力诱导双折射方法 g}]t[}s1]� �?6'rBH�/w 在激光晶体上产生机械应力的同时,产生各向异性密度分布,从而在材料的折射率上产生差异,这是由折射率椭球进行数学上的定义的 (表示为一个椭圆,用来描述光通过材料的不同速度)[6]。在产生光学各向异性元件内行进的不同光速的效果也被称为双折射。这种效应可以用材料折射率椭球Bij的变化来描述[7] ?7{H|sI�� $ImrOf^�qt 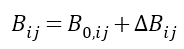 (1) q�e5fek��y V^;jJ'��] 其中,i,j=1,2,3。二阶张量B(0,ij)代表无应力折射率椭球张量,∆Bij代表由于诱导应力产生折射率椭球变化,它可以表示为 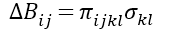 (2) :6�%Z�]t�t 其中,k,l=1,2,3,爱因斯坦的求和规则在这里适用。二阶张量σkl代表了诱导矢量主应力,πijkl是描述每个材料的第四阶压电光学常数张量。通过方程式(1)和(2),当某些压力σkl产生时,我们可以计算折射率椭球张量Bij。然后,可以用下面的关系式来计算介电常数张量ϵij 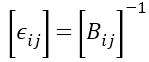 (3) 6-O_�\Cq8� 得到的结果ϵij来进行晶体的后续光学仿真。方程式(1)-(3)在任何坐标系中都成立。然而,需要强调,应用每个方程式的张量时,要用同一坐标系表示。由于晶体材料的对称性,在晶体坐标系中就很容易描述它们的性质,例如,压电光学张量πijkl通常只在这样的系统参考书目中给出[6]。另一方面,在实验室坐标系中,通过实际的晶体几何结构可以便捷描述应力σij,为了后续的光学模拟,需要给出介电常数ϵij。更严格的,我们首先定义两个笛卡尔坐标系统x-y-z和x,-y,-z,分别代表实验室和晶体坐标系统,[aij]作为从实验室到晶体系统的转换矩阵。因为应力通常在实验室系统中用x,y,z来描述,压电张量通常是在晶体坐标系中用x,y,z,给出。为了使用公式(2),这两个量必须在相同的坐标系中表示。为了简易,将二阶应力张量转换到晶体系统,而不是转换四阶压电张量。由于对称性,根据Nye’惯例,应力通常以缩写的方式表达,如σn,n=1,……,6。应用3×3坐标变换矩阵,我们首先将缩写σn明确为σij,然后使用下面的方程 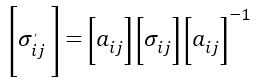 (4) ?IpL�f\�n- 来计算在晶体系统中关于x,y,z,的应力张量。坐标变换不改变对称性,根据Nye’惯例,应力张量σij也可以缩写为σ^,。同样,由于晶体的对称性,使用Nye,惯例[6],方程式(2)中的张量可以缩写,我们可以在晶体坐标系中用x,y,z,改写方程式(2),如下 v$^Z6>v�VI y!�x�E<S&Y 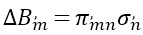 (5) U(x]O/m��� >t7x>_�~
� 其中,m,n=1,……6。实际上,压电光学张量几乎总是以晶体系统中6×6矩阵的缩写方式给出。在计算方程式(5)之后,∆Bm^,可以改写为一个更明确的形式∆Bij^,。接下来,使用方程式(1),包含应力影响的折射率椭球可以计算出来。由于以下事实:1)由等式(5)得到的张量∆Bij^,在晶体系统中给出; 2)无应力折射率椭球张量在晶体系统中有一个简单的对角线形式;我们在晶体系统中进行方程式(1)的计算,得到 K(aJi�,e> 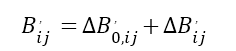 (6) y|wc�,n%L> {s;U~!3aY 其中 ��*g^x*|f6 it�Mg|%B% 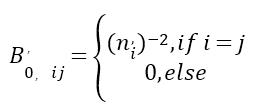 (7) �bV"G~3COy ...... o=1��X^, fD�Sv?cr�v
n'emN��Ra QQ:2987619807 �qg�rg C�J
|