本文介绍了模拟光在均匀介质中传播的四种快速而严格的方法。结果表明,在自由空间传播中,对光滑强相位项的解析处理在减少计算量方面是非常有效的。因此,在不限制快速傅里叶变换算法应用的情况下,我们重新设计了平面波角谱(SPW)算子来处理线性、球形和一般光滑相位项。特别是对于非傍轴场传播,所提出的技术可以显著地减少所需的采样点数量。数值结果表明了新方法的有效性和准确性。 ���me�T~b� 7-.Y��VM~R 一.文章介绍 D�Tk)Y-eQ� &/}]9� ��# 光学建模与设计是研究与开发中极其重要的一部分。由于人们对高质量光学系统(包括衍射光学和微光学、散射物体和部分相干源)的需求日益增加,基于几何光学和物理光学相结合的模拟方法,即场追迹变得非常重要。这种模拟技术的一个重要部分是谐波场在均匀介质中的传播。然而,能够快速、准确地模拟一般光场在自由空间中的传播仍然是一项具有挑战性的任务。常用的算法只能做到快速或者只是准确。 �M�QY^�#N� h�.ojj$f, 在本文中,我们没有进一步的物理近似,介绍了四种新的算法,基于平面波(SPW)算子的角谱,有效地计算包含平滑但强相位项的非傍轴矢量光场的传播。根据光滑相位项的形状,可以使用不同的传播算子。它们的共同点是避免了光滑相位项指数函数的采样。相反,平滑相位项是解析处理的,只需对残差进行采样即可执行传播操作;因此,称为半解析传播技术。 8i=J(�5=�� b"�t95qlL 首先,在第二节中我们给出一个问题的描述并引入数学符号。然后,在第3节中,我们考虑了一个球面相位项,Mansuripur[6]为此引入了一种严格的技术,称为使用快速傅里叶变换(FFT)的扩展菲涅耳衍射积分。在本节中,通过应用Van der Avoort等人最初使用的数值合适的抛物线拟合技术改进了该概念。在另一种情况下[7],详细讨论了扩展菲涅耳算子在数值上可行的参数空间。此外,我们还介绍了扩展的菲涅耳算符的快速反演方法,用于快速计算非傍轴场到焦点区域的传播。 =0TnH<���` }�(�z[
rZ� 在第四节中,我们描述了一个用于光场快速传播的半解析SPW算子,它包含一个光滑的线性相位项。该方法基于线性相位项和横向偏移量的解析处理。之后,我们将这两种技术结合起来,得到了一个数值有效的半解析SPW算子,它能够同时解析地处理线性和球形相位项。 LCx{7bN1ro �la��>:%SD 最后,在第6节中,我们通过将光场分解成具有平滑线性相位项的子光场,将半解析SPW算子概念推广到平滑相位的通用形状。在目标平面上,所有传播子光场被相干地相加,其中解析已知的平滑线性相位项以数值有效的方式使用第7节中介绍的逆抛物面分解技术(PDT)进行处理。数值结果证明了新的传播方法的有效性和准确性。所有的模拟都是用光学软件VirtualLab完成的。 b�2�6#�0;i 3r!6Z5P7{' 二.均匀介质中的场追迹 ��I�3�]-�$ xQ9P'ru�� �Ny��pM+�y 在光场追迹法中,光在线性、均匀和各向同性介质中快速而精确的传播是由谐波场的概念处理的。结果表明,任何电磁场都可以分解为一组谐波场[8,9]。在空间频率域中,以特定角频率ω0振荡的单次谐波场定义为
�q � ��9lz C']TO/�2q� 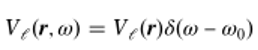
(1)
�e�`zx��#v i"Hec��9Ri 用位置向量
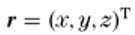
和角频率ω分别表示。请注意,下列理论是完全矢量的,因为在式(1)中,谐波场分量代表三个电场分量和三个磁场分量,由于计算效率高,常用的谐波传播技术基于FFT算法[10]。一种严格的传播技术是SPW算子[5],其中各谐波场分量的复振幅在与传播方向正交的平面边界上,通过傅里叶变换(FT)分解成一组平面波
�B�:#5U85m =�B��<>�H$ 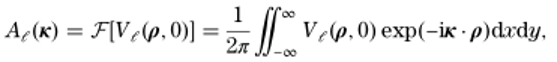
(2)
��gR}>�q4b m/RX~,T*v& 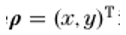
是初始平面边界上的横向位置向量,是
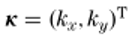
对应的空间频率矢量。用
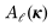
表示的平面波通过与传播因子相乘,在距离z上传播
)zz^R�B\�p 4�^cDp!��8 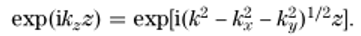
(3)
�'�RK��.w^ CZ"~���N`� 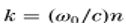
表示折射率为n的均匀介质中的波数,c为光的真空速度。最后,利用逆傅里叶变换将所有平面波叠加,从而得到SPW传播算子,
$Wt0e 4YSu �t&�}Z~�Zp 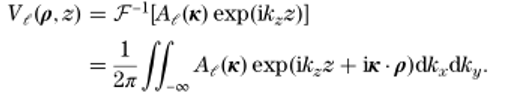
(4)
d�5h]yIz^� ,(&jG^IpVJ 从物理角度来看,SPW算子对任何传播距离z和任何空间频率矢量k[5]都是有效的。然而,对于长的传播距离,采样公式(4)的数值工作量太大。对于非傍轴场,它包含高频分量,数值工作量将变得更高。图1示意性地示出了由于快速增长的数值工作量而导致的SPW算子的有限范围。
4.il4Qqy}i 一篇文献中报道了两个近似公式(4),以克服这一局限性。在这两种情况下,即菲涅耳和远场积分,使用近似来分离球面相位项与积分的数值计算,并且球面相位项是被解析地处理的。这就大大减少了数值计算的工作量。然而,由于这些近似,两种解决方案的适用性受到限制。菲涅耳积分[11]使用空间频率分量的泰勒展开。用这种方法,将式(3)的球面相位函数替换为抛物线相位函数,从而得到式(4)中逆傅里叶变换积分的半解析解。如图1所示,该概念仅适用于具有低空间频率的傍轴场。对于长传播距离z,可以应用远场积分[5],其中公式(4)的逆傅里叶变换积分可以用固定相位的想法来半解析地求解。
QP�/%�+[E. 图1:场追迹中常用的基于FFT的传播算子的有效范围的示意图。灰色区域表示在数值上可行的参数空间。严格的SPW算子在长传播距离或大空间频率下很难突破数值工作量。由于物理近似的性质,远场和菲涅耳传播算子具有有限的有效范围。
C�q�\1t� &N4Jpa}w/% 由于普通的自由空间传播算子使用范围的限制,先进的传播技术的发展对于非傍轴场追迹是必不可少的。这些技术应覆盖图1中剩余的白参数空间,并在精度和数值计算之间取得最佳折衷。文献[2,3,12-14]中有几种方法。然而,这个问题的一般解决办法仍不清楚。在实践中,非傍轴谐波场振幅出现了采样问题,其中部分包含强而光滑的相位项
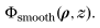
数学表达式为
�ev�~/Hf�� !k�CM�w%[� 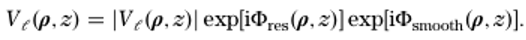
(5)
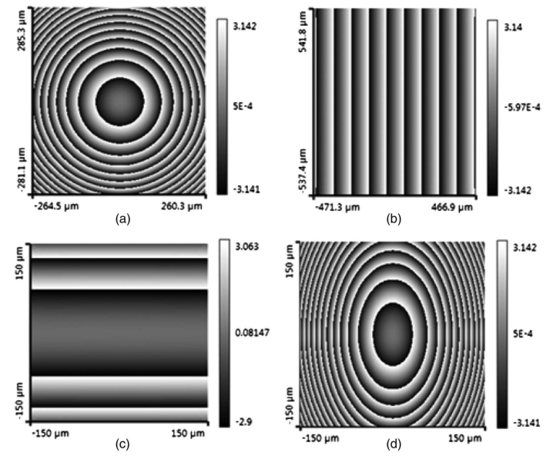
0��kC}qru' ,Vb���;�2� 在这项工作中,我们将开发非傍轴场的自由空间传播技术,包含不同类型的平滑相位项。图2显示了四个光滑相位项的例子,它们起源于光学装置中的不同元件。例如,球面相位项是由光通过
透镜系统的跃迁引起的。在第3节中,我们将介绍一个严格的传播算子,它允许对球相项进行分析处理。之后,我们将在第4节讨论一个改进的SPW算子。这使得能够对线性相位项进行分析处理,线性相位项通常出现在具有任何光偏转的光学建模中,例如通过组件的倾斜。在第5节中,利用第3节和第4节的思想,导出了一个半解析SPW算子,它可以同时解析地处理线性和球形相位项。柱面和像散平滑相位项的存在是相当普遍的,例如在
半导体激光器的激光束整形元件中。在第6节中,我们将推广使用偏微分方程半解析处理光滑相位项的概念。所有操作的评估都是通过一些实际的模拟来完成的。
H����QP��b 三. 半解析SPW算子 %B9ib�y8)1 首先,我们将导出包含光滑球面相位项的场的半解析传播算子。在1989年 MurSuriPur[6]中扩展了经典的菲涅耳传播概念,超过了近轴情形。因此,首先推导了Mansuripur的传播算子。之后,为了进一步提高算子的计算性能,引入了抛物线拟合法,并将其数值效率与基于SPW的传播技术进行了比较。讨论仅限于可传播波,在这种方法中,必须忽略倏逝波,这对于z远大于λ是有效的。从第1节中的SPW传播算符开始,等式(3)中的球相函数可以严格地写成泰勒级数,
�;VM',�40� Gt;@.�jY&�  OS|uZ<"Rq3
OS|uZ<"Rq3 
 A8Z2�o�\+
A8Z2�o�\+ 图2.光滑相位项(2π-模采样)的四个例子在光学建模和设计中非常常见:球面相位项(a)可以通过推广菲涅耳衍射积分进行解析处理,如第3节所示。线性相位项(b)由第4节中的修正SPW算符解析处理。一般的光滑相位项,如柱面波(C)和像散抛物线波(D),可以用PDT进行线性近似分析处理。
在数字上更方便。代替了方程(2)和(4)中的两个FFT, 这两个FFT被用于处理标准SPW算子中数值工作量的巨大光场,修改后的算子执行三个简单的FFT。尽管如此,一个额外的FFT步骤是必要的:二次相位项的解析处理。式(15)导致新算符的数值性能提升。与SPW传播算子相反,增大的传播距离主要是给半解析SPW算子引入一个慢振荡相位项。这种较慢的相位振荡可以减少采样工作。 然而,在等式(8)中由高阶相位函数
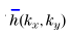
引起的相位振荡仍会随着距离的增加能变大。Mansuripur[6]在其工作中已经提到,通过对kz使用更方便的抛物线拟合方法,而不是如等式(6)中的泰勒展开,可以显著减少高阶的影响。根据抽样原理[15],我们不应关注不是高阶函数本身而是其梯度
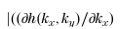
的最大绝对值。通过最小化其梯度
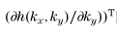
最大值以达到最佳的数值效果。 基于这一思想,Mansuripur在其出版物[6]的附录A中提出了一种先进的拟合方法。然而,它只是
优化抛物线的斜率,而不是顶点偏移。此外,这项技术还需要解一个方程,包括不同指数的幂函数,这只能用数值方法来实现。 一种抛物线拟合方法可以得到更强大的分析方法,van der Avoort等人使用了这种方法[7]在完全不同的背景下。据此,球相函数可以写成
Q�a�*?iD�� �WH:[Y�7D� 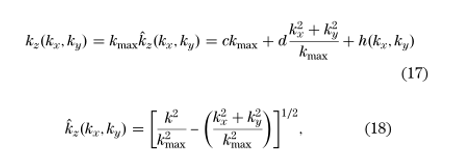 6 0C;J!��D
6 0C;J!��D 相对于最大空间频率Kmax的绝对值进行归一化。式(17)的两个拟合参数由[7]得到
OPm����?kr �6@0
wKV!D 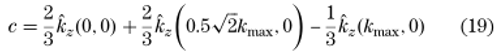 z9> yg�_Q�
z9> yg�_Q� 图3(a)说明了用泰勒展开式的前两个项(式(6)、式(17)的Avoort拟合和Mansuripur的拟合技术对kmax的一维例子的球面相位函数的拟合。相应的高阶相位函数;如图3(b)所示。在这里,Avoort拟合的特征是最小化梯度的曲线,这使得所有高阶相位函数的影响最小。因此,Avoort拟合能做到在公式(8)中仅需求对修改后的角谱进行最小努力的采样。请注意,在低空间频率情况下的不完全Avoort拟合与采样无关,因为它的梯度很小。与Mansuripur拟合相比,本文给出了Avoort拟合的解析表达式。
�s=�)0y$�� �ZH�PsGH�A 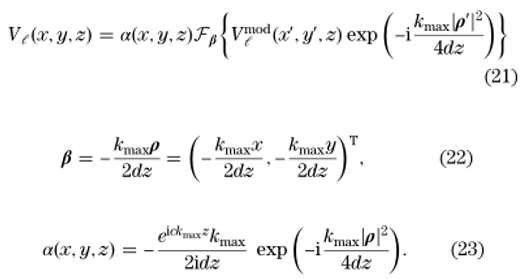 �"v.�]s;�g
�"v.�]s;�g 到目前为止,由式(3)的球形传播核引起的球面相位项用式(21)进行了解析处理。通常情况下,对于直径较小,因而发散较大的场,球面传播核的采样占主导地位。接下来,我们转向光场,在传播之前,光场已经有了一个很强的球面相位。例如,这出现在透镜系统的出射光瞳中。在这种情况下,初始谐波场包含一个强球形相位,并且可以有效地利用半解析SPW传播算子对球相项的数值传播进行反演。为此,公式(21)重新排列为
图3 根据Taylor、Avoort和Mansuripur拟合球面相位函数kz。
(a)一维球函数及其相应的抛物线拟合曲线。
(b)(b)高阶相位函数,从球面函数中减去抛物线拟合函数。
A*B表示卷积积分
aFkxR\x
6% 44�s�
K2�
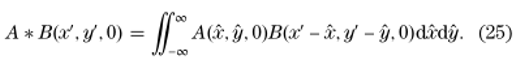 s�U7>q��}! F[aow$",+}
s�U7>q��}! F[aow$",+} ......
{��HgW9�N( QQ:2987619807