基于体全息光学元件可聚焦光伏光谱分裂系统的光栅-透镜

摘要

在光栅-透镜光谱分裂设计中，平面透射光栅设置在平凸透镜的入口处。入射太阳光谱的一部分在偏离透镜法线15-30°处衍射。衍射光谱区域在离轴点处聚焦，而未衍射光谱在透镜的光轴上聚焦。由于衍射波是平面的和离轴的，离轴焦点受像差影响，增加了系统损耗。场曲、色差和球差使用散焦和弯曲焦平面（用每个光伏接收器近似）来补偿。通过修改在构造全息图中使用的离轴波前来校正彗差。在本文中，我们分析了通过共轭对象光束修正离轴波前记录的非平面透射光栅的使用。发散源用作共轭对象和参考光束。球面波入射在透镜处，并且光栅被记录在太阳能集中器的入口孔处。调整轴上光源，在全息图平面上产生轴上平面波前。离轴光源近似为在全息图平面上产生非平面离轴波前的衍射受限光斑。基于平面AM1.5光谱的照明在焦平面上再现离轴衍射受限点。本文介绍了光线追迹和耦合波理论仿真，用于量化通过像差校正实现的损失减少。
关键词：光谱分裂；全息；太阳能；聚焦光伏；像差补偿；光管理；损耗减少

1. 简介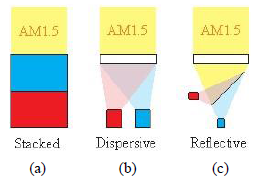

图1.多能隙结构（a）串联（堆栈或垂直）和横向：（b）色散（c）反射

在单光伏（PV）结器件中，低于能隙的光子能量不能被吸收。相反，超过能隙的光子能量被部分地转换成电功率，其余能量在PV器件内被热化。入射到能隙能量的不匹配从根本上限制了（Shockley-Queisser单个能隙极限）单结系统的效率[1]。频谱分裂技术可以根据光谱匹配能隙将入射光子分配到多个结来达到更高的效率[2]。使用光谱分裂系统（SSS），光学系统将入射光子空间上分布到光谱匹配的能隙，以减少入射到能隙能量失配损失。

多结系统通常利用能隙的串联或堆栈（单片）布置来实现，如图1（a）[3]所示。以能隙能量降低的顺序堆叠结，在顶部具有最高的能隙（第一个入射）。上层结作为下层单元的红色通带滤波器。由于结之间的物理接触，串联方法需要子单元的晶格匹配。此外，串联方法具有串联连接的结，将结构限制为具有最低短路电流的能隙。这些约束限制了功率输出并增加了制造的复杂性。

横向SSS在物理上分离了结（如图1（b）和（c）所示），并避免串联结构的限制。光学系统将入射的太阳光分成不同的光谱带来优化每个能隙单元的光谱响应。没有晶格匹配限制，可以使用更广泛类型的PV材料（包括有机物），以便更有效地利用太阳光谱。此外，结优化可以集中于光谱带的完全吸收而不是晶格匹配条件。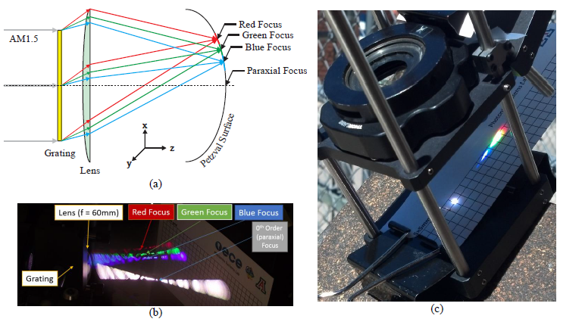

图2.用于光谱分裂的全息光栅-透镜CPV几何结构。原理图（a）、台面和室外（可见光范围）演示原型（分别为b和c）

光栅-透镜光谱分离结构由位于平凸透镜的入口孔径处的平面透射光栅组成。入射光谱的一部分离轴（在15-30°）衍射到透镜中。未被全息衍射的光在轴上进入透镜，并在近轴焦点处会聚。衍射光谱分量进入透镜离轴并且分散在这样一个表面（对应透镜的场曲和全息图的色散特性的表面上）[4]。

光谱分裂系统可以使用具有高光学效率以及良好的反射和透射光谱特性的反射滤波器来实现，如图1（a）所示。尽管已经展示了具有二向色性[5,6]和全息反射滤波器[7]的系统，但是它们具有以下缺点：
 反射方法需要至少N-1个N结滤波器[5,6]，增加了系统复杂性，追迹灵敏度降低了可靠性。
 反射方法需要频谱分裂滤波器在集中照明下操作，以最小化滤波器的所需面积和成本。
 二向色滤波器用于聚光结构的性能随着非垂直入射光束而降低[8]。

使用图2（a）中所示的光栅-透镜几何结构可以避免这些问题，用单个宽带滤波器进行聚光之前分离光谱，从而减小了滤波器上的入射角和功率密度。此外，大型全息光学元件可以使用廉价的材料制造，例如重铬酸盐明胶（DCG）[9,10]和光聚合物[11]。

2. 光谱分裂评价函数

在本节中，定义了评估整个系统及其各个组件的频谱性能的度量。
2.1 光谱转换效率
每个能隙的效率用光谱转换效率（SCE）定义：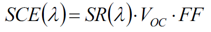

（1）
其中有光谱响应（SR）、开路电压（VOC）和填充因子（FF）（电池参数）[12]。SCE在AM1.5太阳光谱的所有波长上的积分，可得到给定电池总的光-电转换效率：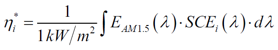

（2）
其中ηi*是全光谱（未滤光）照明EAM1.5下的电池的效率[3]。随着入射光谱被滤波器过滤，SCE可以计算出来和并根据以下公式计算指定能隙的效率：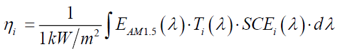

(3)
其中Ti(λ)是滤波器的透射率，ηi是系统的第i个能隙的能隙/滤波器组合得到的效率。

2.2 最佳单能隙上整个系统的效率和改进

对于具有N个能隙的系统，系统总效率由以下表达式给出：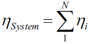

（4）
其中ηsystem是整个频谱分裂系统的效率，ηi在表达式（3）中定义。

根据表达式1至4，显然与全光谱的单结性能相比，光谱分裂将降低单个能隙的效率。由于SSS的目标是使总效率ηsystem大于系统中的最有效能隙，因此有必要定义一个参数以评估对全光谱单能隙电池性能的改进。在本文中，对最佳能隙（IoBB）的改进定义为光谱分裂系统的效率与其最佳（最大全光谱效率）能隙的比率，用以下表达式所描述：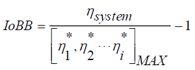

（5）
其中η1*，η2* ...ηi*是在全光谱AM1.5照明下系统中各个能隙的效率。

2.3 滤波器光谱重叠

在小节2.1的分析中的透射率项（T）仅考虑带内理想滤波器的透射率（在关注的能隙光谱范围中的滤波器效率）。比较下面图3中的理想滤波器和实验滤波器，有必要定义频带内和带外性能（与其他系统能隙的串扰）的评估度量。对于本文，使用了实验和理想（方形）滤波器之间的加权SCE频谱重叠。该加权重叠度量随着来自系统中其他光谱滤波器的串扰而减小。对于双能隙系统，该度量描述如下：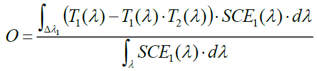

（6）
其中O是上述重叠度量，T1是滤波器对于感兴趣的能隙（SCE1）的透射率，T2是导致串扰的滤波器的透射率。在感兴趣的能隙两个滤波器的透射率评估使用同样的Δλ1波长范围。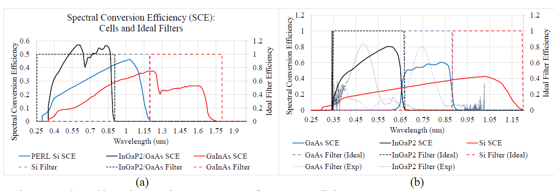

图3.光谱分裂的全息光栅-透镜CPV几何结构

3. 建模和原型系统结果

设计平面透射光栅使用物理光学软件对其进行数值建模，以获得AM1.5照明的光谱和角度性能数据。然后将光栅数值模型放入Photon Engineering FRED®Optimum光线追迹软件中，对整个系统进行建模，并考虑光学和追迹损耗。类似地，用实验测试的光栅的衍射效率替代数值模型。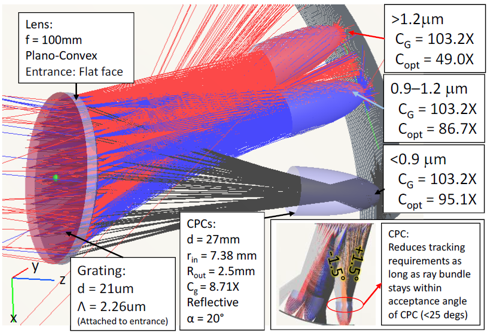

图4.在可见光中的一个能隙和在近红外中的两个能隙的SSS的模拟。插入记录显示追迹误差分析。

使用高性能PV电池数据[3,5,6,13,14]和遵循表达式1至6，具有在可见光（<0.9μm）中一个能隙和在NIR中两个能隙的结构（系统1）。另外一个结构是在可见光范围内两个能隙和在NIR中一个能隙（系统2）。

经计算，系统1的总效率为33％。考虑菲涅耳反射、衍射、串扰和CPC（复合抛物面聚光器）的损耗，转换效率降低到29％。如果还考虑±1.5°追迹误差，则会产生额外的1％的损耗。对于系统1，发现最差情况IoBB为17％。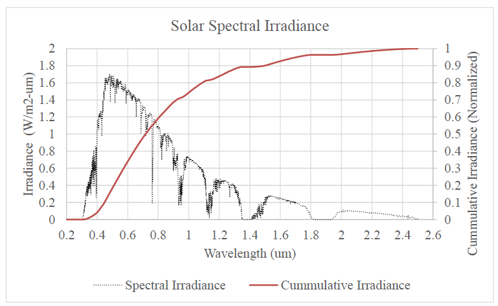

图5.太阳的光谱辐照度，累积辐照度（∞能量）已经归一化为1kW / m2。

在图5（红色）中检查累积光谱太阳辐射，约80％的可用太阳能波长范围低于硅的能隙（>1.1μm）。光谱分裂系统在此波长范围中IoBB比率大于NIR。通过比较表1中系统1和系统2的结果，表明具有较大可见光谱覆盖的系统的最坏情况IoBB为47％，超过系统1的IoBB的2.5倍。
表1 （左）NIR光谱分裂系统（右）可见光光谱分裂系统分析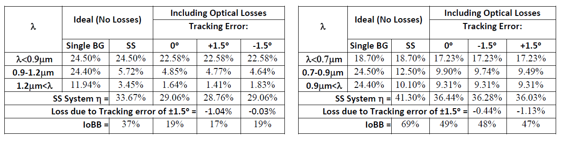

若要获得表1的模拟值，实验滤波器需要O = 0.55（系统1）和O = 0.76（系统2）的权重叠值。已经获得具有O = 0.35的原型滤波器（系统2），产生的IoBB > 10％。

3.1 追迹和光学损耗

全息光栅的衍射效率性能的数值模拟包括AM1.5照明下的离轴入射角，偏离法线的角度最高达到±1.5°，以模拟追迹误差。

追迹误差分析总结在图6中。对于通过光栅条纹和非垂直入射（达到+1.5°）的正方向的追迹误差，衍射角和透镜场曲耦合的变化产生最坏情况损耗（>1％净效率下降）。当追迹误差朝向法线（-1.5°）时，发生相反的情况（衍射角变化补偿透镜场曲）。衍射和场曲的耦合/补偿可以在上面的表1中的“Loss due to Tracking”值中看到。追迹误差引起的损耗对于沿着光栅条纹方向的角度变化是类似的。

在图6中，还可以看出不管追迹误差如何，点列图显示出显着的彗差图案。由于大角度处较大的波长衍射，因此随着波长增加，彗差的影响更明显，如图6中点列图的“尾部”的增加宽度和图1（c）中的原型的衍射图案所示。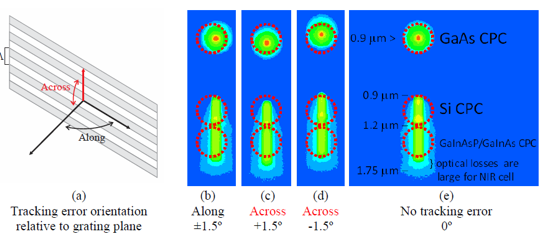

图6.在图4的焦平面处的追迹误差（±1.5°）

3.1.1 彗差和能隙位置补偿

通过非平面构造几何形状，可以实现彗差补偿。在共轭方向上使用两个球面波束（点光源），取代在（实）传播方向上的两个平面波前（如图7的顶部所示）。参考点源位于透镜的近轴焦点处，物光源位于所需的接收器位置，如图7的底部所示。记录几何形状的共轭还允许调整接收器的位置（如平面焦平面）。[/td][/tr][/table][/td][/tr][tr][td]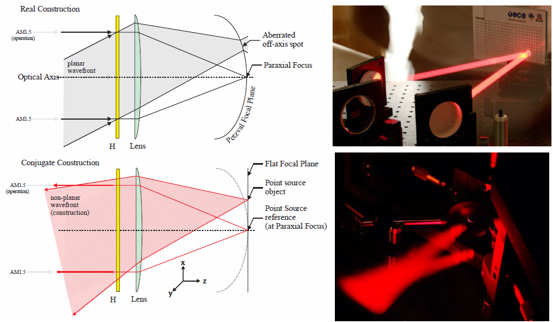

图7.真实的全息记录（左上），用于补偿彗差并将接收器（能隙）定位在平坦表面上的共轭结构（左下）。

近轴焦点处的参考点光源由透镜转换成平面波前。相反，物点光源被透镜转换成有像差的准平面波前。通过在透镜的平面上记录具有准平面波前的光栅来校正该效应。
通过在平坦表面上使用期望的点源对象光束，来调整接收器的位置，如图7的左下几何结构所示。

图8.在左边，采用真实结构（平面光栅）记录的光栅重建，分别对应于（a）单色光（633nm的HeNe）和（b）白光（氙弧太阳模拟器）。在右侧，采用共轭结构（补偿光栅）记录的光栅重建，分别对应于（c）单色光和（d）白光。

图8（a）和（c）的比较显示出彗差的共轭结构补偿，将光引向更紧密的焦点。对于单色和白光重建可以看到类似的结果。
4. 结论
在本文中，讨论了光谱分裂作为用于多结PV系统的串联电池的替代。提出了频谱转换效率（SCE）、整体系统效率、滤波器加权重叠（O）和对最佳能隙（IoBB）的改进，并将其定义为光谱分裂系统的评估度量。描述了全息光栅-透镜几何结构，并已经给出模拟和实验结果。对于在可见光范围（<0.9μm）中具有更多能隙的系统，IoBB显示较大值。
光栅-透镜几何结构的离轴衍射角导致彗差和显着的系统损耗。提出并演示了使用共轭记录几何来补偿这种损耗的方法。
正在进行的工作包括使用系统度量结合已建立的用于全息光学元件中的最小化像差技术来增加总体光电转换效率。
5. 致谢
作者想要感谢NSF / DOE ERC合作协议号EEC-1041895、NSF批准号0925085、亚利桑那州TRIF（WEES）项目和研究公司的支持。
参考文献

[1] T. O. M. Tiedje, E. L. I. Yablonovitch, G. D. G. D. Cody, and B. G. B. G. B. G. Brooks, “Limiting efficiency of silicon solar cells,” IEEE Transactions on Electron Devices 31(5), 711–716 (1984) [doi:10.1109/TED.1984.21594].[2] A. Barnett, D. Kirkpatrick, C. Honsberg, D. Moore, M. Wanlass, K. Emery, R. Schwartz, D. Carlson, S. Bowden, et al., “Very high efficiency solar cell modules,” Progress in Photovoltaics: Research and Applications 17(1), 75–83 (2009) [doi:10.1002/pip.852].
[3] M. A. Green, K. Emery, Y. Hishikawa, W. Warta, and E. D. Dunlop, “Solar cell efficiency tables (version 42),” Progress in Photovoltaics: Research and Applications 21(5), 827–837 (2013) [doi:10.1002/pip.2404].[4] E. Hecht, Optics 4th edition, in Optics 4th edition by Eugene Hecht Reading, MA: … (2001).
[5] A. L. Gray, M. Stan, T. Varghese, A. Korostyshevsky, J. Doman, A. Sandoval, J. Hills, C. Griego, M. Turner, et al., “Multi-terminal dual junction InGaP<inf>2</inf>/GaAs solar cells for hybrid system,” in 2008 33rd IEEE Photovolatic Specialists Conference, pp. 1–4, IEEE (2008) [doi:10.1109/PVSC.2008.4922575].[6] J. D. McCambridge, M. A. Steiner, B. L. Unger, K. A. Emery, E. L. Christensen, M. W. Wanlass, A. L. Gray, L. Takacs, R. Buelow, et al., “Compact spectrum splitting photovoltaic module with high efficiency,” Progress in Photovoltaics: Research and Applications 19(3), 352–360 (2011) [doi:10.1002/pip.1030].
[7] D. Zhang, M. Gordon, J. M. Russo, S. Vorndran, M. Escarra, H. Atwater, and R. K. Kostuk, “Reflection hologram solar spectrum-splitting filters,” K. VanSant and A. P. Plesniak, Eds., 846807–846807–10 (2012) [doi:10.1117/12.929187].[8] B. Mitchell, G. Peharz, G. Siefer, M. Peters, T. Gandy, J. C. Goldschmidt, J. Benick, S. W. Glunz, A. W. Bett, et al., “Four-junction spectral beam-splitting photovoltaic receiver with high optical efficiency,” Progress in Photovoltaics: Research and Applications 19(1), 61–72 (2011) [doi:10.1002/pip.988].
[9] E. D. Aspnes, J. E. Castillo, R. D. Courreges, P. S. Hauser, G. Rosenberg, and J. M. Russo, “Volume Hologram Replicator for Transmission Type Gratings,” U.S. Patent No. Application US 2013/0120815 A1, in WO Patent …, United States (2013).[10] R. K. Kostuk, J. Castillo, J. M. Russo, and G. Rosenberg, “Spectral-shifting and holographic planar concentrators for use with photovoltaic solar cells,” in Proceedings of SPIE 6649, M. Symko-Davies, J. Guo, B. von Roedern, D. R. Myers, and A. E. Delahoy, Eds., p. 66490I–66490I–8, San Diego, CA (2007) [doi:10.1117/12.736542].
[11] D. Jurbergs, F. Bruder, F. Deuber, T. Fäcke, R. Hagen, T. Rölle, M. Weiser, A. Volkov, B. M. Llc, et al., “New recording materials for the holographic industry,” 1–10 (2009) [doi:10.1117/12.809579].[12] M. Gordon, D. Zhang, S. Vorndran, J. M. Russo, C. K. Luscombe, S. E. Shaheen, and R. K. Kostuk, “Planar holographic spectrum-splitting PV module design,” High and Low Concentrator Systems for Solar Electric Applications VII 8468(520), K. VanSant and A. P. Plesniak, Eds., 846808–846808–9 (2012) [doi:10.1117/12.929387].
[13] J. Zhao, A. Wang, M. A. Green, and F. Ferrazza, “19.8% efficient ‘honeycomb’ textured multicrystalline and 24.4% monocrystalline silicon solar cells,” Applied Physics Letters 73(14), 1991 (1998) [doi:10.1063/1.122345].[14] G. J. Bauhuis, J. J. Schermer, P. Mulder, M. M. A. J. Voncken, and P. K. Larsen, “Thin film GaAs solar cells with increased quantum efficiency due to light reflection,” Solar Energy Materials and Solar Cells 83(1), 81–90 (2004) [doi:10.1016/j.solmat.2003.11.030].
[15] K. Winick, “Designing efficient aberration-free holographic lenses in the presence of a construction-reconstruction wavelength shift,” Journal of the Optical Society of America 72(1), 143 (1982) [doi:10.1364/JOSA.72.000143].

文章来源：Grating-Over-Lens Concentrating Photovoltaic Spectrum SplittingSystems with Volume Holographic Optical Elements

查看本帖完整版本: [-- 基于体全息光学元件可聚焦光伏光谱分裂系统的光栅-透镜 --] [-- top --]