元件的位置和方向

1. 描述
 利用光路图定义光源辐射、光学元件结构以及探测器。
 用户定义光通过光学系统的路径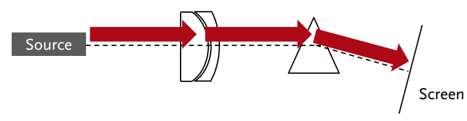

 通过该案例，介绍了光路图中光学元件如何确定位置和方向这个用户案例解释了，在光路图（LPD）中光路元件的位置和方向怎么使用。

2. 光路图与实验室对比

 实验室中的光学器件
— 光源
— 光学组件
— 探测器或光学效应探测器
 光路图中的元件：
— 辐射源模型(VirtualLab中称为光源)
— 真实的光学组件
— 理想的光学组件
— 探测器
— 分析器
 实验室中的组件不必通过光路图的中的一个组件进行表达

3. 光路元件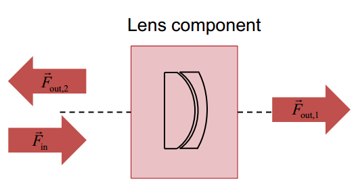

 光路元件可以采用多个输入和输出通道。
 输入与输出通道定义的轴线应与光学系统的光轴一致。
 输入通道应与来自不同方向/元件的入射光分布相一致。
 输出通道应与传播到不同方向/元件的出射光分布相一致(如反射和透射光)。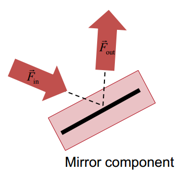

 通道的轴线可以预设或者根据元件的参数进行改变。
 每一个元件都可确定其相对于各通道轴线的方向。

4. 元件位置的定义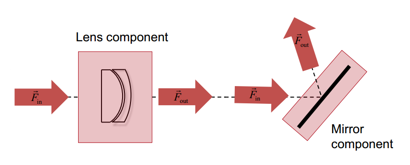

 一个元件的一个输出通道的轴线应与另一个元件或探测器的一个输入通道的轴线相连接。
 所有相连的元件及其对应的通道轴线共同定义了系统的光轴。
 光路中的元件都有绝对位置。
 绝对坐标系的原点由光源决定。
 光源在原点处，没有倾角。
 对于元件的位置，可使用相对位置/角度或绝对位置/角度来定义。

 每个组件对每个通道定义了多个参考点。
 通过测量参考点间的距离可确定元件的相对位置。

5. 位置和方向确定规则
 远离元件的方向距离都是正。
 元件的位置和方向可以在元件编辑对话框中直接编辑，也可在坐标断点元件的帮助下实现。
 每种元件类型都有已定义的参考点可供选择。(只有编程的元件可以选择任意参考点)

6. 方向与位置的坐标系统
 一个连续元件的位置和方向可通过设置x,y,z的偏移量来确定，这个偏移量是入射通道坐标系的原点对于最后一个元件的输出坐标系的关系。同样，倾角也是与最后一个元件的输出坐标系统有关。(可选择不同的角度定义)

7. 输出通道的方向
 反射通道对应入射光线的反射部分。透射输出通道与透射光也是如此。
 但是，各通道坐标系统的Z轴方向与光线传播的主方向之间没有确定的关系。
 根据反射定律，在入射通道坐标系统的XY平面上，计算反射通道的方向。这样做的目的是对多样的反射光方向得到一个好的初步预测。
 对于标准系统，默认方向是合理的并确保很小的计算量。对于特殊情况，其他方向可能更有用，并且必须使用坐标断点元件帮助定义。

8. 输出通道的自动方向