| infotek | 2021-11-30 08:54 |
理解并使用复合直方图一个复合直方图是标准直方图的扩展,其显示了一个实部和虚部分别具有确定范围的复数场中数据点的个数。(“数据面源”) 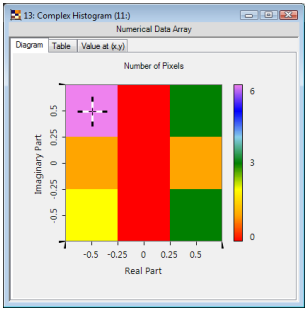 在本示例中,在实部范围为-0.75~ -0.25,虚部边界为0.25~0.75的区域上有6个数据点。 2. 采用的示例数据:随机位相分布 振幅 位相  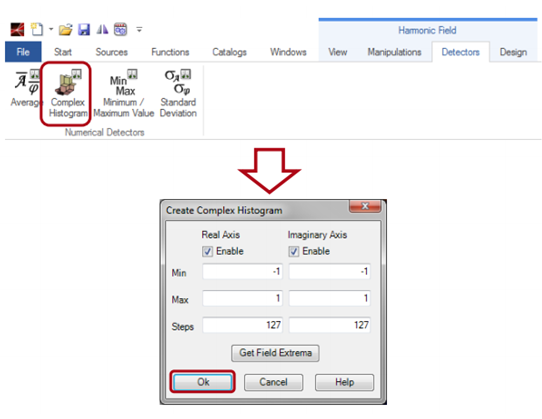 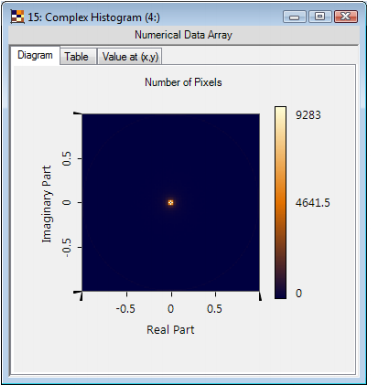 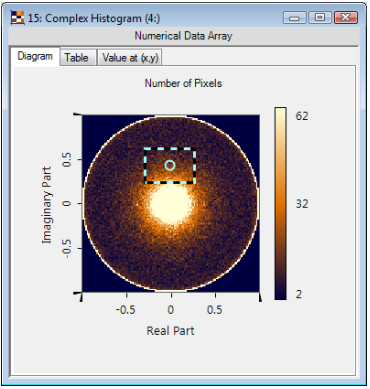 在暗区域随机建立一个矩形标记 点击视图 基于选择缩放 6. 解释:振幅  7. 解释:振幅  相位值分布均匀 - 如预期的随机相位分布。 8. 调整复合直方图:初始的  9. 调整复合直方图:嵌入  10. 调整复合直方图:更大的“格子”  11. 量化效果 8阶振幅硬量化结果  8阶相位硬量化结果   |
|