| infotek | 2021-11-22 09:25 |
傅里叶变换光谱仪在FRED中建立光谱仪 为了简化过程,使用一个理想的点光源、理想的透镜和理想的分束表面(图1)。详细的扩展光源、真实的镜头、分束器或线栅分束器可以纳入其中使之用于更加实际的分析。 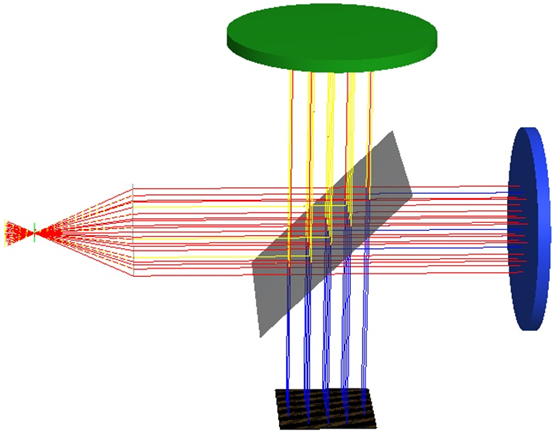 图1 简单的傅里叶变换光谱仪模型,由一个点光源、理想透镜和具有可移动反射镜的迈克尔逊干涉仪组成。来自光源的准直光束被送入到50/50的分束器上。反射光传播到一个固定的反射镜(绿色),透射光传播到一个平移反射镜(蓝色)。来自两个路径的光经过分束器后重新组合,收集到的能量在(黑色)探测器处测量。 FRED模型的第一步是创建一个相干的点光源对象。接着,创建一个光谱并分配给光源。光谱可以从文本文件导入、图片的数字化取样或者由特定的函数(高斯或黑体)计算得到。使用FRED“lens Module”表面类型构成的“自定义元件”对象,可以创建理想透镜,透镜位于距离点光源10mm处。“lens Module”表面具有10mm的焦距和5mm的半孔径。接下来,使用与准直光束成45度角的平面表面创建理想分束表面。创建了自定义“50/50”分束涂层(图2)并应用到该表面。 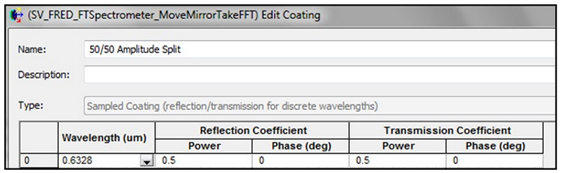 图2 自定义50/50分束涂层规格。如果指定一个单一波长,则涂层将同样适用于光源的所有波长。 系统中的两个反射镜是通过两个FRED的“Mirror”对象,它们都具有“反射”涂层和“反射所有”光线追迹控件。每个反射镜位于距离分束器20mm处,一个在+y方向上平移,另一个在+z方向上。最后,在垂直于分束器的组合光束方向上,添加一个吸收表面和对应的分析面,模型就完成了。 运行光谱仪重现光源光谱 在初始结构中,干涉仪两光束路径具有相同的路径长度,即光程差(OPD)为零。为了收集光源的光谱信息,一个反射镜必须移动一些距离来改变OPD。在反射镜的移动的每一步中,落到探测器上的功率将会被收集。由此产生的探测器功率和OPD的图像,称为干涉图,并将会经过一个快速傅里叶变换(FFT)来确定光源功率和光空间频率。为了自动运行这一过程,可以创建一个嵌入式脚本(写在FRED内置BASIC中)来移动反射镜和收集探测器的值。 在下面的例子中,平移反射镜用1024步移动了总距离为0.04mm。由于FFT算法的缘故,步数必须为2的幂次。分辨率越高,产生的频谱越准确。低分辨率的反射镜扫描会有干涉图欠采样的风险。欠采样的干涉图会导致FFT中的低频混淆。光谱作为“均匀间隔、根据光谱加权”分配给光源,充分的采样光谱同样重要。在这个例子中,使用的波长采样的最大数目为256。欠采样的光源光谱在重现的光谱中会产生余弦条纹。 例1:单波长光源 给定光源1.5μm的单一波长。该波长对应666.7(1/mm)的空间频率。单波长的干涉图是一个简单的余弦函数。(图3) 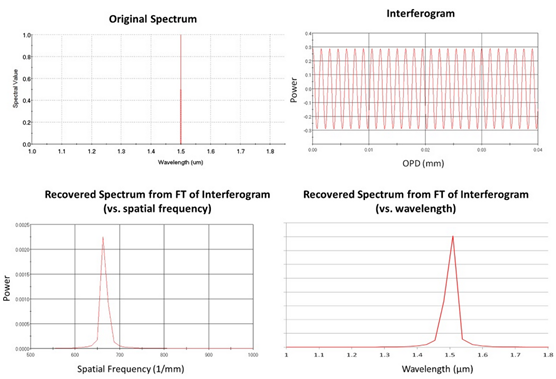 图3 由FTS获得的单波长光源光谱。左上:绘制的初始光源光谱vs.波长(μm)。右上:探测器功率vs. OPD的干涉图。左下:重现光源光谱vs.空间频率(1/mm)。右下:重现光源光谱vs波长(μm)。 例2:高斯光谱 光源给定为高斯光谱,具有0.555μm的中心波长和0.0589μm的半极大半宽。中心波长对应于1801.8(1/mm)的空间频率。注意到重现的光谱具有明显的不对称性(图4)。这是因为光谱是波长的高斯函数,空间频率是波长的倒数。较短的空间频率间隔对应于较大的波长范围;因此,重现的频谱的左半将出现更多的压缩(图4)。 图4 由FTS获得的高斯光源光谱。左上:初始光源光谱vs.波长(μm)。右上:探测器功率vs OPD的干涉图。左下:重现光源光谱vs.空间频率(1/mm)。右下:重现光源光谱vs波长(μm)。 例3:白光LED光谱 给定光源一个白色荧光LED的光谱特性。该光谱在波长= 0.45μm处有一个尖峰,在波长= 0.65μm处有一个宽峰。蓝色峰对应于2222.2(1/mm)的空间频率。红色峰对应于1538.5(1/mm)的空间频率。注意重现的光谱形状被水平翻转(图5)。这是因为光谱是波长的函数,空间频率是波长的倒数。另外,相对于原光谱的红色峰,重现的光谱显示出更高的低空间频率值。这是因为低空间频率的间隔对应于一个较大的波长范围,在这些空间频率处,更多的光功率将被收集。 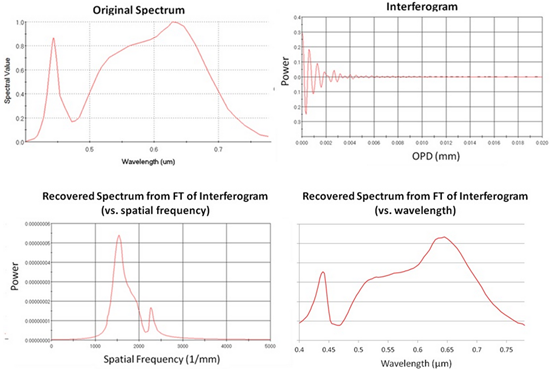 图5 由FTS获得的白色LED光源光谱。左上:初始光源光谱vs.波长(μm)。右上:探测器功率vs. OPD的干涉图。左下:重现光源光谱vs空间频率(1/mm)。右下:重现光源光谱vs.波长(μm)。  |
|