| infotek | 2021-10-12 09:29 |
OptiMode:矢量有限元法-精度及优势由于光通信系统向集成化方向发展,因此高折射率对比度以及亚波长尺寸波导的建模变得越来越重要。这些属性需要一个模态求解器,既能够真实地进行几何近似,也可以进行电场的近似。波导尺寸与感兴趣的电磁场区域可能有几个数量级的差别,如长距离等离子体激元。 1. 应用 硅光子学 波导设计 空心光纤 亚波长光学 弯曲波导 长距离等离子体激元 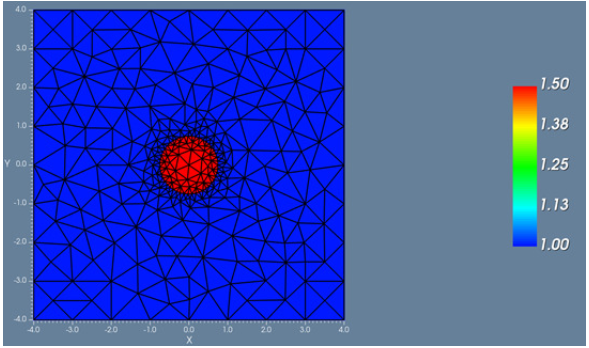 高折射率对比光纤 矢量有限元法速度非常快,而且精度高 全矢量公式化各向异性模式求解器 能够使用5阶插值混合向量/节点量,以去掉伪解并极大的增加精度 可利用布局的对称性降低仿真域尺寸 单轴完全匹配层(UPML)可以用来找到遗漏的模式 三角网格大小可调整以精确近似电磁场和波导的几何结构 模态指数评估可提高速度,还可以用来搜索特定的光学模式 采用变换光学精确地计算弯曲波导的模式,,即使是一个很小的曲率半径 3. 仿真描述 在矢量有限元法与其他模式求解器进行对比之前,应对不同的阶数的基础函数的准确性进行了测试。最简单的波导是一个均匀介质微波波导。纤芯是一个简单电介质,包层被视为一个完美的电导体,以描述一个矩形金属墙。 下面的图标中显示了VFEM结果和解析结果间的相对百分比误差。误差根据有限元网格中自由度结果的方程进行绘制。 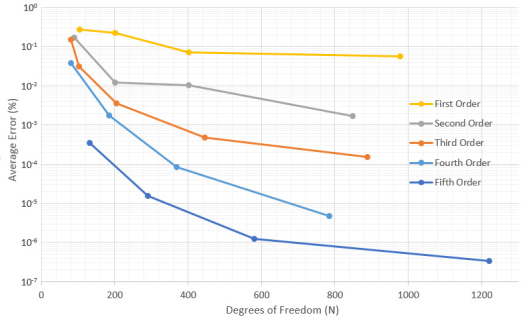 图1.VFEM计算的平均误差 前5个模式误差的平均值如图1中所绘制。其清晰表明,对于一个传播常数,增加基础方程的阶次可以获得更高精度的结果。在x=400时,增加基础方程的级次,等于近乎提高数量级高度的精度。此处应该指出的是,最大平均误差仅为0.3%。 对一个纤芯折射率1.5和包层折射率为1.0的高对比光纤,对比使用不同方法的模态求解器。尽管在SOI波导中可能不算是高对比度,但对于我们来说对比度已足够大了。波导的横截面显示在反面。 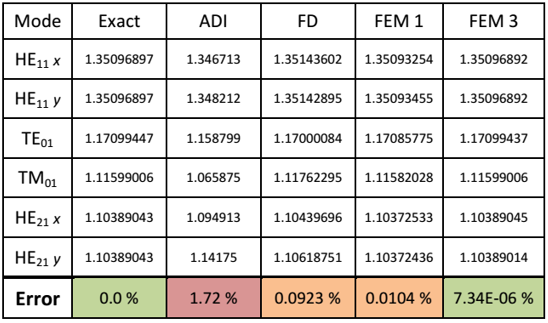 表1:利用多种模态求解器计算的模折射率。包含了模折射率的平均误差。 上面的表格显示了对于前六光纤矢量模式计算的模折射率。将一个光纤矢量求解器作为基准,并标签为“Exact”。此外,ADI、FD和FEM求解也都用于计算光纤模态。其中FEM分为两组:第一组使用1阶量,第二组使用3阶量。但在表格中没有给出各求解器所花费时间。其中,FEM计算时间与FD的计算时间大概一致,(FD耗时~109秒,FEM耗时~65秒)。 表格充分说明了FEM模态求解器的优势和ADI的不足。ADI方法计算速度快,但是寻找较高精度高阶模态比较困难,而且其精度随波导对比度提高而降低。FD法优于ADI,但精度最好的是FEM法。这并不仅对于光纤模态,对于矩形和任意形状波导也同样适用。 有限元求解器如此精确的主要原因之一是其近似几何体的方式。ADI和FD采用小矩形进行折射率采样,这导致了对角线或曲线的阶梯式近似。理论上,矩形晶元可以缩小至阶梯式以进行一个很好的近似,但在实践中它仍然会导致相当大的误差。有限元求解器使用三角形网格可以近似对角线到一个高精度水平,并可以提供足够少的三角来近似曲线。 QQ:2987619807 |
|