| infotek | 2020-12-15 09:21 |
FRED数字化极坐标数据取样本文讨论了如何使用FRED数字化工具对极坐标数据采样。一个典型的应用是使用厂商规格表上的强度分布来为一个光源指定光线的方向。当条件允许时,最好是使用一个光线集(也就是厂商测试光线数据)来代替规格表上的模型。当近场分布可以忽略时,这种方式是较为合适的。 光源创建 通过强度(功率/立体角)的形式,从极坐标图中我们将会创建光源,但极坐标图定义的仅仅是光线的方向。在没有任何额外数据或者光线信息的条件下,我们对于这些光线的空间分布一无所知。因此,我们做出这样的假设:光线随机分布在光源出口孔径的空间范围内。 步骤1:创建光线网格位置 假设光源出口孔径的大小是2mm×1.2mm(W×H),首先鼠标右键单击光源文件夹,从列表清单里选择“创建新的详细光源”。在光源对话框的位置/方向标签上选择“随机平面(平面上排列着随机点)”,并根据上述的规格表设置X和Y的外半孔径值。开始后,设置光线数目为1000,孔径的形状为矩形。 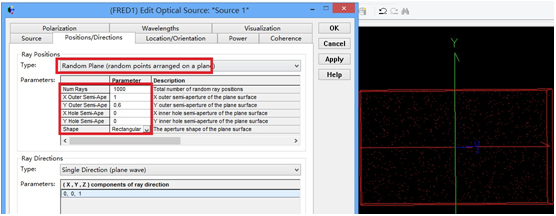 步骤2:指定光线的方向类型 光线的空间位置指定好了后,我们需要输入光线的方向信息。规格表为光源提供了强度数据,因此使用光线方向说明“Randomly according to intensity distribution”才是有意义的。该光线方向说明将会在球形极坐标网格上获取强度分布,并且根据该分布轮廓统计随机的光线方向(比如:强度最高的地方产生更多的光线,强度低的方向光线较少)。 在光源对话框位置/方向标签下的光线方向区域处,选择方向类型“Randomly according to intensity distribution”。 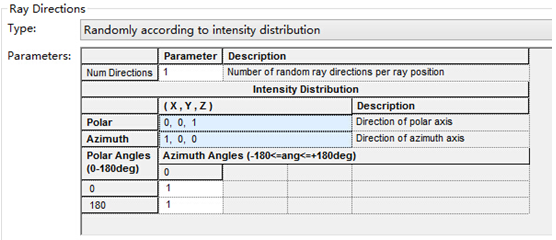 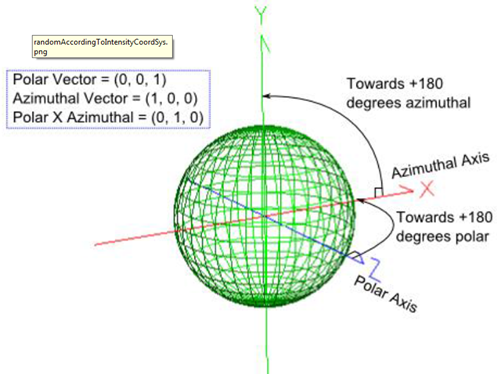 步骤3:数字化极坐标图数据 为了从极坐标图中数字化取样数据到光线方向规格表中,我们可以在电子表格区域右键点击鼠标,在列表菜单里选择“数字化曲线”。 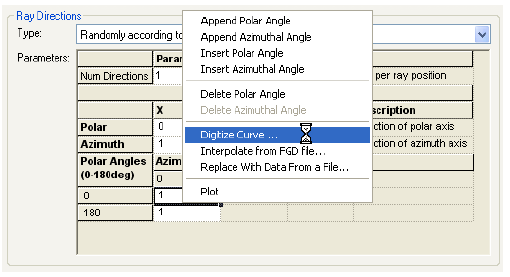 在数字化工具对话框中使用“选择图像”按钮,从规格表中选择一个极坐标图的图像文件。FRED数字化工具允许的图像文件格式是*.bmp, *.pcx, *.jpg, *.tga, and *.tif。 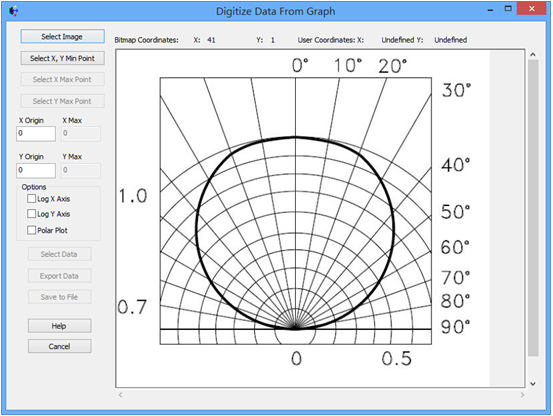 随着图像文件载入到数字化工具中,选择“极坐标图”选项。  在极坐标图的情况下,X和Y满足极坐标的条件: 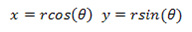 分别沿着X和Y轴,它们的取值范围为0到1。 接着,点击“选择X,Y最小值点”按钮,然后在极坐标图中选择rho=0,theta=0的点。在下面的图中,0,0点是蓝色的。 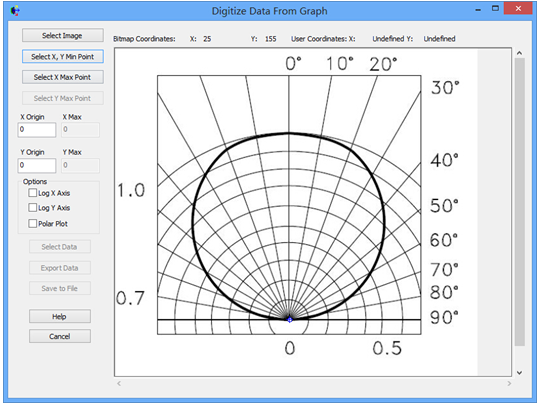 下一步,点击“选择X最大值点”按钮。选择X轴的一个点(不一定是最大值),然后输入相应的值到“X最大值”文本框中。 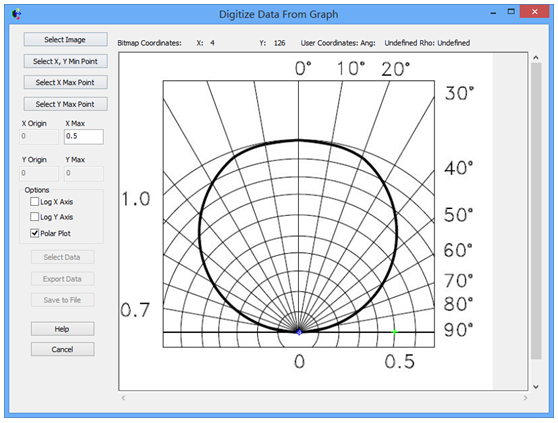 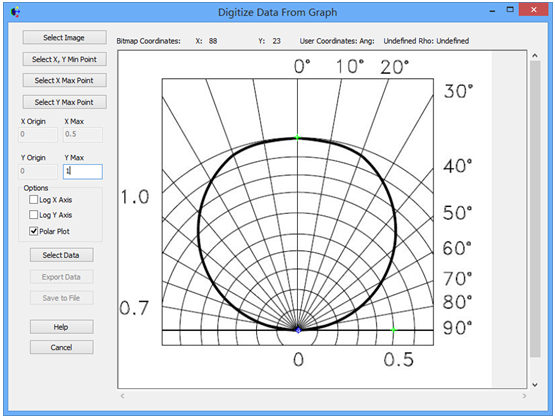 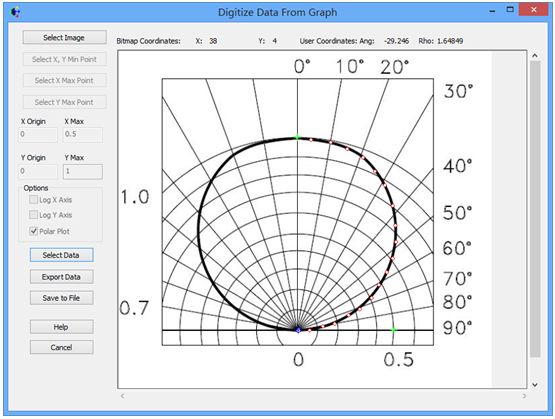 一旦我们在极坐标图中选择好了这些点,点击“导出数据”,就会将数字化的点送回到光线方向对话框中。 步骤4:验证强度分布 既然数据已经从极坐标图中导出,那就有必要验证坐标系统的设置是否正确。在本例中,极轴沿着Z方向,方位角轴沿着X方向。当只有1个方位角数据输入进来时,FRED将假定分布是旋转对称的。当输入多个方位角数据是,FRED会将这些数据点进行线性插值。 多方位角的输入方法:如下图,在此区域右键然后选择”Append Azimuthal Angle” 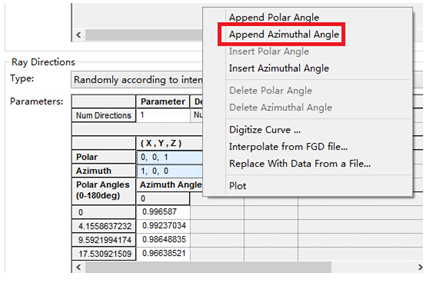 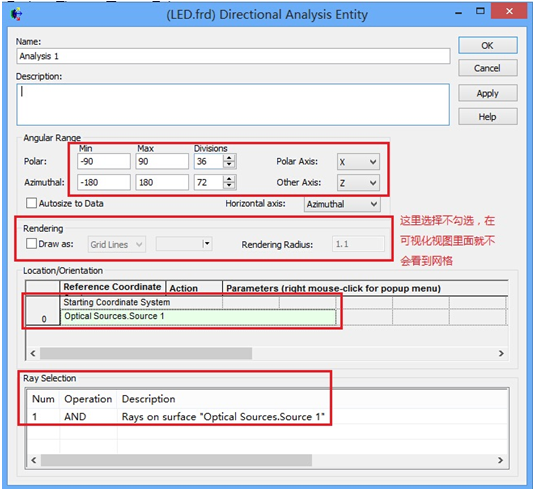 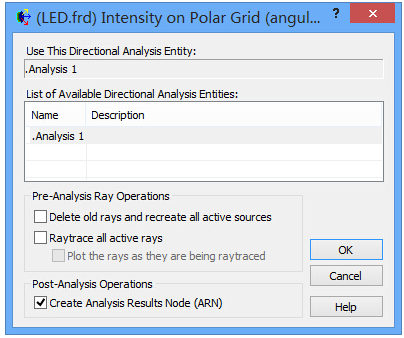 图表显示出来后,在树形文件夹中最下面的Analysis Results会发现一个新的节点“Intensity 1”, 选中此节点,点击鼠标右键,在弹出的列表菜单中选择“以可视化视图显示”(接受默认设置)。该选项将会以三维视图呈现连贯的强度分布,并且实现简单的验证:模型中的强度分布是正确取向的。本实例系统在光源处含有一百万束光线,其强度分布图如下所示。 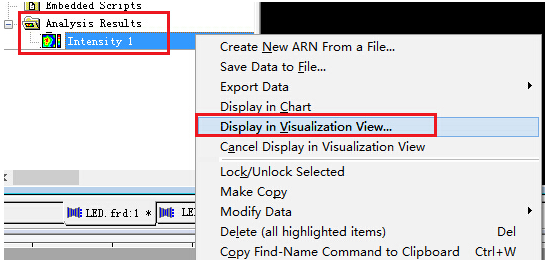 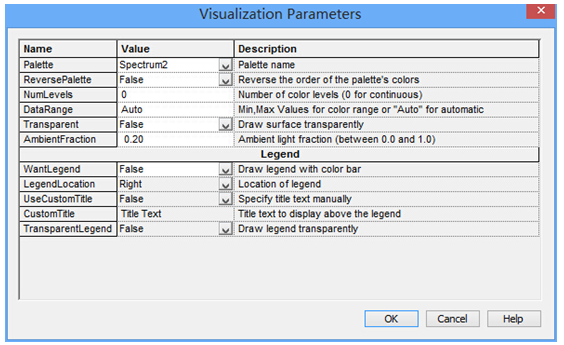 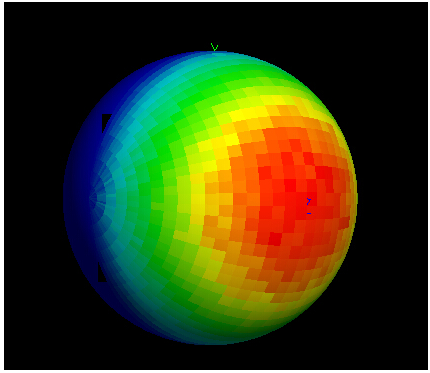 总结 1. FRED数字化取样工具不仅可以取样光源数据,还可以取样材料、模型、镀膜数据、散射数据; 2. 在验证光源的光强度分布或照度分布的时候,不要去追迹光线,在raytrace菜单下选择 Create All Source Rays,然后点击照度分析或强度分析即可。  QQ:2987619807
|
|