| infotek | 2020-09-30 11:17 |
GLAD:共焦非稳腔模拟仿真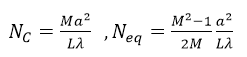 (11.1) (11.1) 其中,a是孔径半径,L为腔长,λ为波长,M是准直倍率。相应的参数数值为:L=90cm,a=0.3cm,M=2,λ=10μ。带入后计算得:Nc=2,Neq=0.75。 激光在腔中来回一次后,分布的单位是初始时的两倍。要开始另一次来回传输,单位需要缩放到原来的单位,根据Siegman和Miller理论,每个来回损耗大约为44%。 GLAD的计算与该理论相符甚好。 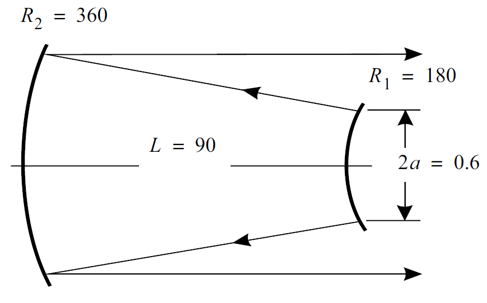 参考文献 A. E. Siegman and H. Y. Miller, “Unstable Optical Resonator Loss Calculations Using Prony Method,” Appl. Opt. Vol. 9, No. 12, p. 2729 (1970). C 谐振腔参数 ---------------------------------------- 等效菲涅尔数 0.5 放大倍率 2 腔长 90cm 孔径1半径 0.3cm 孔径2半径 0.6cm ----------------------------------------- ## ENEGY/GNORM 归一化每一次传递之后的光束能量为分配的值 ## pass_number变量是为了计数宏运行次数,同时作为标题输入参数 ##变量stop用于测试收敛,并将值传递到if语句以退出宏 ###变量field_radius用于在宏结束后初始化数组并重新调整场半径 variable/dec/int pass_number # 声明pass_number变量为整数 variable/dec/int STOP TEST # 声明确定收敛的开关 ####定义一个宏,它是一系列命令,通过空腔表示一个循环 macro/def conres/over # 声明宏conres /新信息覆盖旧信息 pass_number = pass_number + 1 list #增量计数器 clap/cir/no 1 .3 # 孔径1 定义 mirror rad=180 # 凸面反射镜,曲率半径r=180 prop 90 # 向后传播90cm mirror rad=360. # 凹面镜 clap/cir/no 1 .7 # 孔径2定义 prop 90 # 向前传播90cm variable/set Energy 1 energy # 将光束的能量存在变量Energy write/screen/on # 写屏 udata/set pass_number pass_number Energy-1 #储存光束能量的变化量 gain/converge/test ibeams=1 nstore=STOP # store convergence test in STOP # gain/eigenvalue/show 1 # 显示本征值 energy/norm 1 1 #光束能量进行归一化 if STOP macro/exit # 条件退出 if [!TEST] then #TEST值为0, 执行语句 title resonator mode pass = @pass_number plot/l xrad=.75 endif macro/end ###初始化变量 pass_number = 0 # 往返次数初始化为0 # field_radius = 1.6 #调整场半径 c##建立初始单位和高斯场分布 array/set 1 128 #设置矩阵为128*128 units/field 1 field_radius # 定义单位 wavelength/set 1 10. # 定义波长 gain/converge/set eps1=.005 eps2=.001 npoints=3 #能量收敛准则的分数变化设置 c#调用宏请求最多30个传递,并在收敛条件下退出 gain/eigenvalue/set 1 plot/screen/pause 3 TEST = 1 resonator/name conres #设置谐振腔名字 resonator/eigen/test 1 #寻找本征值 TEST = 0 pass_number = 0 #往返次数初始化为0 clear 1 0 #光束初始化为0 noise 1 1 #从噪声开始 resonator/run 30 #宏运行30次 title ex 11: energy per step #设置图形的标题 plot/watch ex11a_1.plt #设置图形窗口的名称 plot/udata max=0 #设置横坐标范围 ###绘制汇聚场分布 title ex 11: resonator pass no. @pass_number #设置图形的标题 plot/watch ex11a_2.plt #设置图形窗口的名称 plot/liso 1 xrad=.75 ns=64 obs 1 .3 title ex 11: outcoupled beam #设置图形窗口的名称 plot/watch ex11a_3.plt plot/liso 1 xrad=.75 ns=64 c##应用透镜并传播到远场 lens/sph 1 100 prop 100 title ex 11: far-field pattern #设置图形窗口的名称,画出远场模式 plot/watch ex11a_4.plt plot/liso 1 ns=64 c###生成环围功率表 encircled/calculate/energy 1 encircled/udata 1 title ex 11: encircled energy plot/watch ex11a_5.plt # plot/udata 1 min=0. max=1. # end 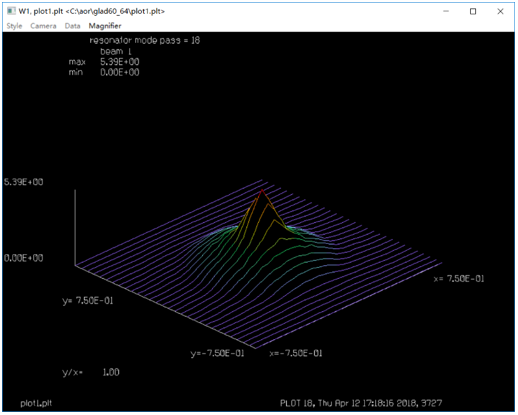 图1.刮刀镜镜前会聚横模 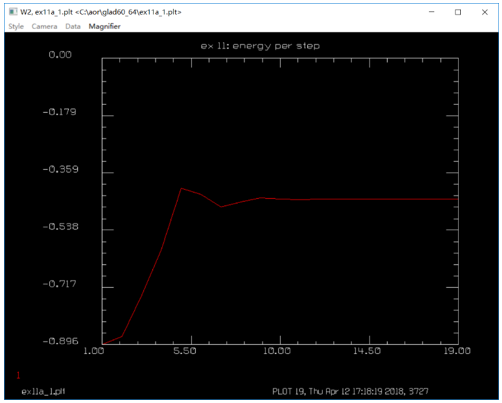 图2.单程能量损失图 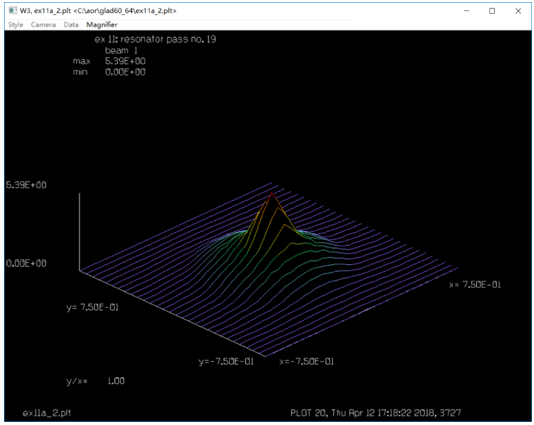 图3 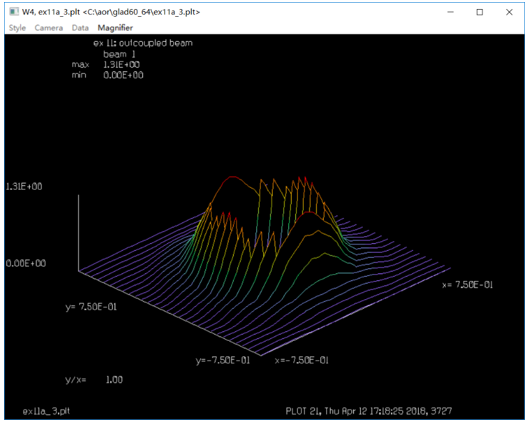 图4.刮刀镜镜后会聚横模 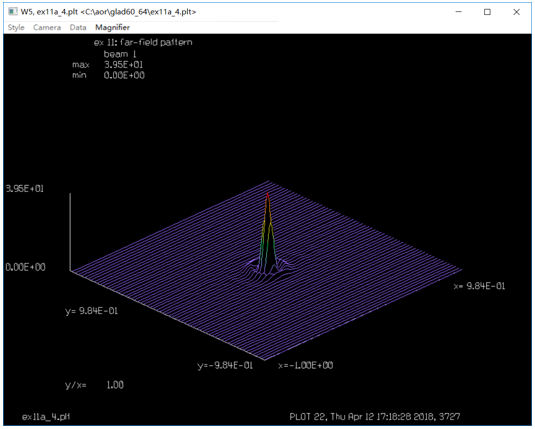 图5.准直谐振腔的远场分布 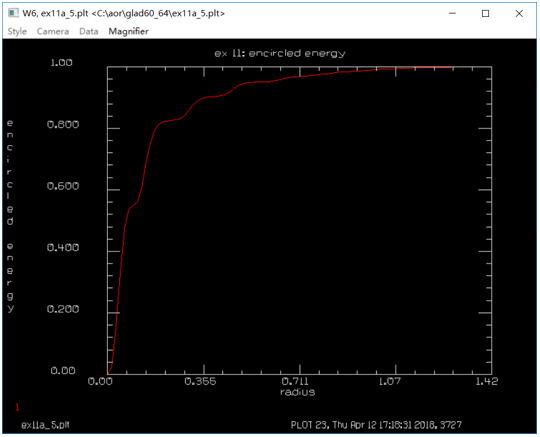 图6.使用PIB命令的包围圆能量曲线 QQ:2987619807
|
|