参数优化研究+光线追迹失败校正:SYNOPSYS 光学设计软件
RZO�5=L�9E
在本课中,我们将探索一个功能强大但很少使用的SYNOPSYS功能:它可以进行参数研究,显示两个变量对第三个变量的影响。在这种情况下,我们希望了解镜头优化运行的结果如何取决于初始结构。 在一个理想的设计中,每一个起点都将达到最佳可能的最佳状态,但现实并不如此。 对于任何给定的问题,通常存在许多局部最小值,并且我们可以期望的最好的优化算法应该可靠地到达最接近的算法。 (当然有所谓的全局优化算法,例如DSEARCH,这和局部优化算法不同。在这里,我们将分析从给定初始结构开始到优化评价函数的过程。) �Wr>(#*r7q
因此,人们会期望两个几乎完全相同的初始结构将达到相同的局部最小值,即使它不是全局的。 当前算法在此优化上的表现如何? TU Delft的Florian Bociort博士发现了一些非常有趣的结果。 他做了一个很简单的例子,如下图所示。 ?U�_9��{}r
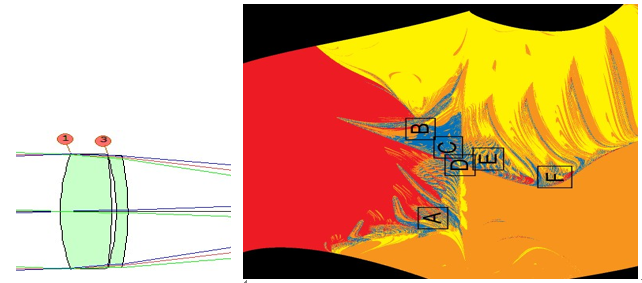
为了使工作变得非常简单,他只在主波长的三个视场点校正了光线,忽略了边缘误差。 然后,他以曲率半径2和曲率半径3的起始值为变量做栅格,并绘制一个图,其中网格上每个像素的颜色编码评价函数的最终值。 他发现有几个局部最小值,即使对于如此简单的问题也不足为奇 - 但完全出乎意料的是,在许多地方,评价函数以非常混乱的方式变化。 因此,附近的起点经常会到达截然不同的终点。 (他在Code-V上做了这个分析。)这是他在 http://homepage.tudelft.nl/q1d90/FBweb/fractals.html 上的文章中的一个图解。 dv7�<AJ��
(我们将这张照片放在了一边,以便它与下面的SYNOPSYS分析一致。) bD�<qNqX�$
注意吸边界附近的结果是非常复杂和混乱的。 黑色区域显示出光线光线失效的起点,因此无法进行分析。
-4fl�V D�
我们认为SYNOPSYS中的PSD算法比上面使用的方法更可靠和稳定,因此我们在3参数评估功能PA3上设置了运行。 这是输入: 8Mu;�U3cIW
Starting doublet: �Ys�P/p-��
.^�[�_���V
RLE %9o+zg? RJ
ID FLORIAN STARTING DOUBLET '�'��S&e�
WA1 .5876000 ��5���h8o4
WT1 1.00000 Z)&D`RCf�
APS 1 /A�PcL5:=
UNITS MM ~�O:
U|&�
OBB 0.000000 3.00000 16.66670 0.00000 0.00000 0.00000 16.66670 0 AIR .0|��=[��|
1 CV 0.0146498673770 TH 10.34600000 =x0No�*#|'
1 N1 1.61800000 ��$�%PVJs�
1 GID 'GLASS ' ��K�m�3&�N
2 RAD -174.6512432672814 TH 1.00000000 AIR @�u)
'y��S
2 AIR v�G
V����d
3 RAD -80.2251653581521 TH 2.35100000 �=MLf[�� �
3 N1 1.71700000 w�qD�5d�
�
3 GID 'GLASS ' 1$ML��#5+,
4 RAD -111.8857786363961 TH 92.41206276 AIR `.=sTp2rbc
4 AIR �g�:��<?�
4 CV -0.00893769 \t3qS
eWc/
4 UMC -0.16667000
u1cu]Sj0
4 TH 92.41206276 gUV���n;_�
4 YMT 0.00000000 M3pj�Xc�<O
5 CV 0.0000000000000 TH 0.00000000 AIR U,;��xZ�e�
5 AIR �MJ\[�D�t�
END 6�T+������
STORE 5 :�g�I.l1��
:Q@�)*k�QH
And this is the input for the PA3 program): 0oU=Rb�C��
ON 78 ! use finer grid (118x118 points) 使用更精细的网格(118x118点) ���!e3YnlE
PA3 LOOP COLOR ! initialize PA3, request color boxes for output初始化PA3,设置输出颜色框 wAYB� RY[�
RZ1 -.025 .04 ! set the range of variable Z1设置变量Z1的范围 h qmSE�'�8
RZ2 -.045 .075 ! set the range of Z2设置Z2的范围 =�Q(vni83<
RZ3 0 5.5 ! display results over this range of merit function values @Bs�0Avj�.
在此评价函数值范围内显示结果 R$m�`Z+/@�
NOSMOOTH ! there will be steps in the output; do not smooth �9"sDm}5%�
按步输出; 结果不会很平滑 fS��A)G$b]
XLAB "2 CV -.025 .04" ! define the label for the X-axis, which is variable Z1 f9TV%fG�?
定义X轴的标签,即变量Z1 Ip?�]K*s�q
YLAB "3 CV -.045 .075" ! label for Y-axis, Z2 Y轴,Z2的标签 !�gP0ndRJ=
ZLAB "MERIT" ! label for Z-axis, the final merit function Z轴的标签,最终的评价函数 O~�@fXMthh
LOOP �
k0H#�:c}
! tell PA3 to loop over the above raster of data告诉PA3循环上面的数据栅格 �)�1F<��6R
GET 5 ! get the starting lens each time每次都得到初始结构的始镜头 ;s�Pz�OS9�
2 CV = Z1 ! set curvature 2 to the value of variable Z1将曲率2设置为变量Z1的值 x��&=9P e(
3 CV = Z2 ! and CV 3 to Z2, using the artificial-intelligence parser 4MW ]�EQ-�
CV 3到Z2,使用人工智能解析器 PR�s@��zkO
PANT ! initialize the variable list初始化变量列表 Z�zj0\?�Ul
VLIST RAD 2 3 ! and vary two radii 两个不同的半径 Tby,J�
B^U
END U�Q�T'6* !
! end of the variable list 变量列表的结尾 HIf{Z* mb�
AANT ! initialize the merit function definition初始化评价函数定义 orIQ~pF#��
GSR .5 10 3 P 0 ! correct a sagittal fan, three rays, on axis 在轴上修正一个光扇图,三条光光线 zAScRg$:?
GNR .5 1 3 P .75 ! correct a full grid of rays, primary color, 0.75 field point l@~L�V}�BI
校正完整的光线网格,原色,0.75视场点 -5>NE35Cto
GNR .5 1 3 P 1 ! same, at full field. 全区域相同 ��UUtbD&�\
END ! end of merit function definition 评价函数定义结束 q'S
=�Eav8
GAEO��$�e:
DAMP 10000 ! initial damping (see below) 初始阻尼(见下文) lDc;__}Ws�
SNAP 50 ! watch what happens, but not too often, in order to keep it fast i�$U�Qb�d�
观察发生状况,但不要太频繁,以保持高效 7#�-y-B]l�
SYNOPSYS 100 ! optimize until it converges 优化到收敛 �c��-CYdi@
Z3 = MERIT ! assign the current merit function value to variable Z3 PA3 告诉PA3循环到下一个案例。 }z�M�f�7<C
! tell PA3 to cycle to the next case. 告诉PA3循环到下一个案例。 8Smj�ZpQ?�
SR7j\1a/2A
为什么高阻尼? (默认值为1.0或0.01,具体取决于模式切换。)SYNOPSYS中的第一次迭代是用DLS(阻尼 - 最小二乘法)循环法,我们希望避免在该算法的第一次传递时产生的任何混乱; 高阻尼将确保镜头在该过程中变化很小。 更强大的PSD算法追迹从传递到传递的一阶导数的变化,并推导出关于高阶导数的信息。 这是PSD方法背后的技巧,但它只能在第二遍开始。
Xm�_�$
dZ
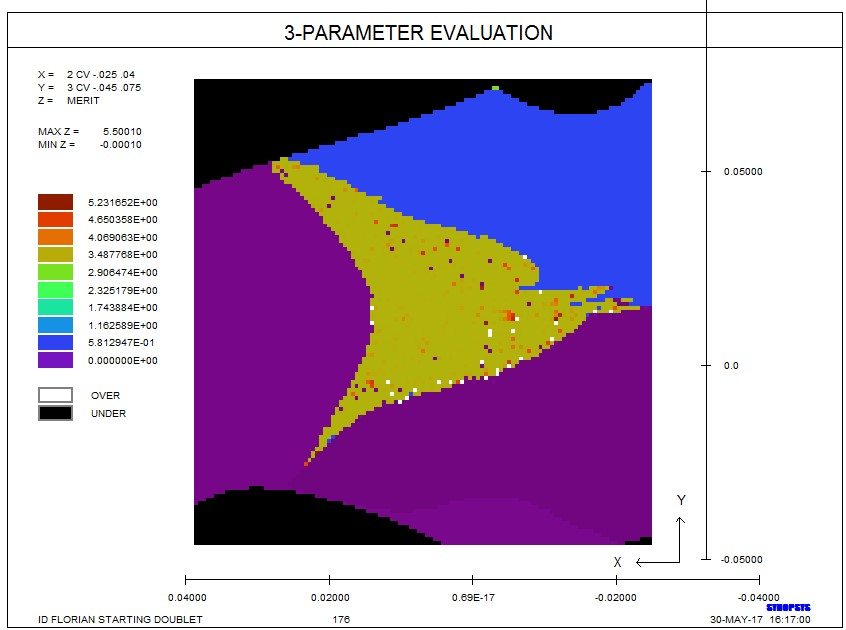
该研究的结果如下所示。 左侧和底部附近的紫色区域显示该程序在不同的初始点上达到相同的最小值 - 而在Florian的研究中,这些区域达到了不同的最小值。 在相交的边界没有明显的混乱,正如我们所期望的那样,PSD方法就是这种情况,尽管在中央绿色区域出现了散乱的极点。 我们将后者归因于第一遍中DLS方法所做的非零更改。 实际上,如果我们用不同的初始阻尼再次运行,那些随机点出现在不同的地方。 �;IZ��?19Q
顶部和底部的黑色区域显示了起点产生光线失效的位置,与他们在Florian研究中所做的相同。 我们很好奇如果我们激活仅在SYNOPSYS™中发现的自动光线故障校正功能会发生什么。 我们将SYNOPSYS命令更改为 �v�R��hnX�
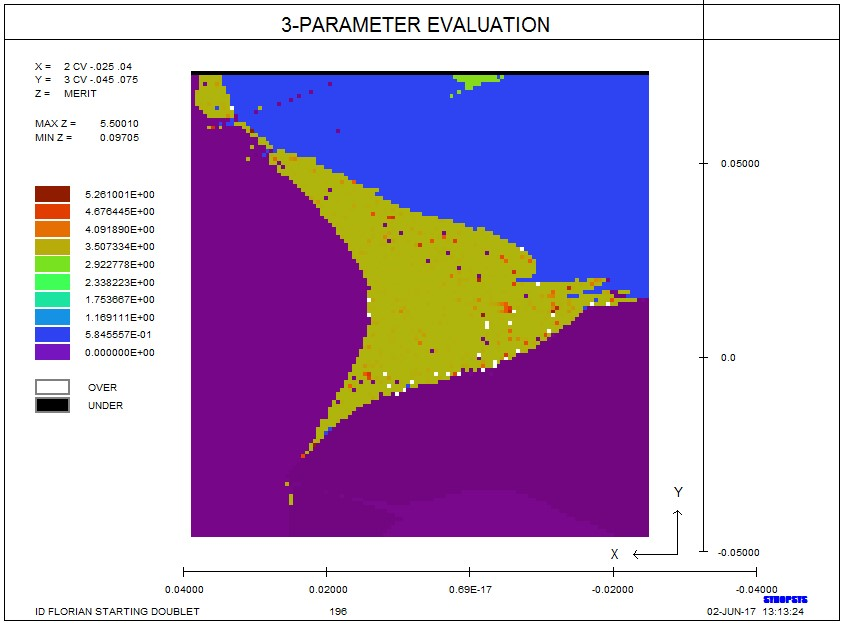
SYNOPSYS 100 0 FIX ;+Y�i.Q/\�
�8���i���0
并重新运行这份工作 (f1M'w/O�D
现在我们看到该程序已经纠正了之前发生过的每一个故障。Florian无法优化的初始镜头现在都能产生可观的解决方案。 现在,在以前全黑的区域的边界处有一些非常轻微的混乱,我们将其归因于更改了光线失效校正程序对该起点的影响。 这些变化有时会使镜头更接近另一个相交的区域。 �?�S#\K^��
这项非常简单的研究只涉及两个变量的优化。 如果我们将CV 1添加到变量列表会发生什么? ]=�&L�_(34
试试看吧!(边界有些偏移,散乱的斑点不再出现。) �6yIvaY$KR
详情请咨询:sales@asdoptics.com 027-87582688 uV]ULm#,i�
|